Еще одним известным классом фракталом являются стохастические фракталы, которые получаются в том случае, если и итерационном процессе случайным образом менять какие-либо его параметры. При этом получаются объекты очень похожие на природные — несимметричные деревья, изрезанные береговые линии и т. д. Двумерные стохастические фракталы используются при моделировании рельефа местности и поверхности моря.
Существуют и другие классификации фракталов, например деление фракталов на детерминированные (алгебраические и геометрические) и недетерминированные (стохастические).
Сложные фракталы
Фактически, если вы увеличите маленькую область любого сложного фрактала а затем проделаете то же самое с маленькой областью этой области, то эти два увеличения будут значительно отличаться друг от друга. Два изображения будут очень похожи в деталях, но они не будут полностью идентичными.
Сравните, например приведенные здесь картинки множества Мандельброта, одна из которых получена при увеличении некоторой области другой. Как видно, они абсолютно не являются идентичными, хотя на обоих мы видим черный круг, от которого в разные стороны идут пылающие щупальца. Эти элементы повторяются бесконечно долго во множестве Мандельброта в уменьшающейся пропорции.
Детерминистские фракталы являются линейными, тогда как сложные фракталы таковыми не являются. Будучи нелинейными, эти фракталы генерируются тем, что Мандельброт назвал нелинейными алгебраическими уравнениями. Хороший пример - это процесс
Zn+1=ZnІ + C,
что является уравнением, используемым для построения множества Мандельброта и Жулии второй степени. Решение этих математических уравнений вовлекает комплексные и мнимые числа. Когда уравнение интерпретируется графически на комплексной плоскости, результатом оказывается странная фигура, в которой прямые линии переходят в кривые, появляются хотя и не без деформаций, эффекты самоподобия на различных масштабных уровнях. При этом вся картина в целом является непредсказуемой и очень хаотичной.
|
|
Рис а. Приближение множества Мандельброта
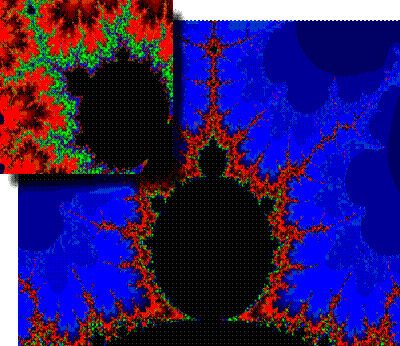Как можно увидеть, смотря на картинки, сложные фракталы действительно очень сложны и их невозможно создать без помощи компьютера.
Практически каждая точка на экране компьютера как отдельный фрактал. Во время математической обработки, каждая точка рассматривается как отдельный рисунок. Каждой точке соответствует определенное значение. Уравнение встраивается, применительно к каждой точке и производится, к примеру 1000 итераций.
Большинство фракталов, которые мы видим сегодня, красиво раскрашены. Возможно фрактальные изображения получили такое большое эстетическое значение именно благодаря своим цветовым схемам. После того, как уравнение посчитано, компьютер анализирует результаты. Если результаты остаются стабильными, или колеблются вокруг определенного значения, точка обычно принимает черный цвет. Если значение на том или ином шаге стремится к бесконечности, точку закрашивают в другой цвет, может быть в синий или красный. Во время этого процесса, компьютер назначает цвета для всех скоростей движения.
Обычно, быстро движущиеся точки закрашивают в красный цвет, тогда как более медленные в желтый и так далее. Темные точки, вероятно, самые стабильные.
|
|
Сложные фракталы отличаются от детерминистских в том смысле, что они бесконечно сложные, но, при этом, могут быть сгенерированы очень простой формулой. Детерминистские фракталы можно построить вручную. Можно построить решето Серпинского до 5 итерации без каких-либо затруднений, что невозможно сделать с множеством Жулиа.
МНОЖЕСТВО МАНДЕЛЬБРОТА
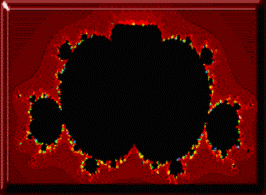
Рис. б. Множество Мандельброта
Множества Мандельброта и Жулиа, вероятно, два наиболее распространенных среди сложных фракталов. Их можно найти во многих научных журналах, обложках книг, открытках, и в компьютерных хранителях экрана. Множество Мандельброта, которое было построено Бенуа Мандельбротом, наверное первая ассоциация, возникающая у людей, когда они слышат слово фрактал. Этот фрактал, напоминающий чесальную машину с прикрепленными к ней пылающими древовидными и круглыми областями, генерируется простой формулой Zn+1=Zn a + C,
где Z и C - комплексные числа и а - положительное число.
Множество Мандельброта, которое чаще всего можно увидеть - это множество Мандельброта 2й степени, то есть а=2. Тот факт, что множество Мандельброта не только Zn+1= Zn І + C, а фрактал, показатель в формуле которого может быть любым положительным числом ввел в заблуждение многих.
Вы видите пример множества Мандельброта для различных значений показателя а.
Рис. в. Появление пузырьков при a=3.5
Также популярен процесс
Z=Z*tg(Z+C).
Благодаря включению функции тангенса, получается множество Мандельброта, окруженное областью, напоминающей яблоко. При использовании функции косинуса, получаются эффекты воздушных пузырьков. Короче говоря, существует бесконечное количество способов настройки множества Мандельброта для получения различных красивых картинок.
|
|
МНОЖЕСТВО ЖУЛИА
Удивительно, но множества Жулиа образуются по той же самой формуле, что и множество Мандельброта. Множество Жулиа было изобретено французским математиком Гастоном Жулиа, по имени которого и было названо множество. Первый вопрос, возникающий после визуального знакомства с множествами Мандельброта и Жулиа это "если оба фрактала сгенерированы по одной формуле, почему они такие разные?" Сначала посмотрите на картинки множества Жулиа. Достаточно странно, но существуют разные типы множеств Жулиа. При рисовании фрактала с использованием различных начальных точек (чтобы начать процесс итераций), генерируются различные изображения. Это применимо только ко множеству Жулиа.
Рис. г. Множество Жулиа
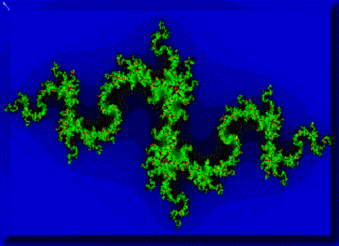Хотя это нельзя увидеть на картинке, фрактал Мандельброта - это, на самом деле, множество фракталов Жулиа, соединенных вместе. Каждая точка (или координата) множества Мандельброта соответствует фракталу Жулиа. Множества Жулиа можно сгенерировать используя эти точки в качестве начальных значений в уравнении
Z=ZІ+C.
Но это не значит, что если выбрать точку на фрактале Мандельброта и увеличить ее, можно получить фрактал Жулиа. Эти две точки идентичны, но только в математическом смысле. Если взять эту точку и просчитать ее по данной формуле, можно получить фрактал Жулиа, соответствующий определенной точке фрактала Мандельброта.
Понятие «фрактал» неразрывно связано с понятием хаос.
Хаос возникает в динамических системах, когда для двух очень близких начальных значений система ведет себя совершенно по-разному. Хаос — это отсутствие предсказуемости.
Фракталы определяют структуру хаоса. Фракталы, по существу, являются новым языком, дающим описание форм хаоса, они позволяют анализировать тонкую структуру хаоса и даже обнаружить в нем проявления порядка. Тонкая структура фрактала может быть следствием и причиной сложного хаотического поведения.
Нa фазовой плоскости такому поведению соответствует замкнутая кривая, называемая аттрактором (от английского глагола to attract - притягивать) - множество траекторий, характеризующих установившийся процесс. В случае нелинейного маятника могут возникнуть сложные, непериодические колебания, когда траектория на фазовой плоскости не замкнется за сколь угодно долгое время. При этом поведение детерминированной системы будет внешне напоминать совершенно случайный процесс — это и есть явление динамического или детерминированного хаоса. Образ хаоса в фазовом пространстве — хаотический аттрактор — имеет очень сложную структуру: это фрактал. В силу необычности свойств его называют также странным аттрактором.
Структура определяет поведение. Фрагментарная, фрактальная природа ежедневной реальности остается за пределами нашего сознания. Чтобы использовать мышление для сортировки явлений и научиться понимать смысл происходящего, мы должны, прежде всего, найти основную структуру реальности. Структуру, вскрывающую порядок, который лежит в основе хаоса.
Существует четыре нелинейные функции, которые помогают нам определить этот порядок в нашем собственном сознании. Ученые, исследующие хаос, обнаружили, что кажущиеся хаотичными, не подчиняющимися никаким законам процессы, и действительности, следуют скрытому порядку. Порядок, который они открыли, четырехкратный: все внешние явления действуют в соответствии с тем, что они называют четырьмя аттракторами - силами, которые извлекают порядок из беспорядка. Они называются
· точечным аттрактором,
· циклическим аттрактором,
· аттрактором торас и
· странным аттрактором.
Эти четыре аттрактора формируют основную структуру внешнего мира, характер поведения и движения рынка.
Точечный аттрактор - это простейший способ привнести порядок в хаос. Это единственное состояние, к которому стремится система в общем случае при бесконечном времени.
Циклический аттрактор – характеризуетсядвижением взад-вперед, подобно маятнику или циклическому магниту. Он притягивает, затем отталкивает, затем опять притягивает и т. д.
Такого рода аттрактор характеризует, например, рынок, заключенный в коридоре, где цена движется вверх и вниз в определенном диапазоне в течение некоторого промежутка времени. Этот аттрактор более сложен, чем точечный аттрактор и является основной структурой для более сложного поведения. Одна деятельность автоматически ведет к другой в повторяющемся порядке. В природе его можно наблюдать на ряде примеров, например, в системах «хищник — добыча», где размер популяции соответствующих хищников или их жертв увеличивается и уменьшается в обратном соотношении. На рынке зерна это явление носит годичный характер. Один год, для которого были характерны высокие цены, порождает увеличение посевных площадей следующей весной, что, в свою очередь, приводит к низким ценам. Затем фермеры уменьшают посевные площади, чтобы добиться более высоких цен.
Аттрактор торос - третий, более сложный, вид аттрактора, характеризуется сложной циркуляцией, которая повторяет себя по мере движения вперед.
По сравнению с циклическим и точечным аттракторами, аттрактор торас вводит большую степень беспорядочности и его модели более сложны. На этом уровне, предсказания носят более точный характер, а модели имеют тенденцию казаться более законченными. Графически он выглядит как кольцо или рогалик. Он образует спиралевидные круги на ряде различных плоскостей, и иногда возвращается сам к себе, завершая полный оборот.
Его основная характеристика - это повторяющееся действие. Он имеет тенденцию создавать что-то вроде беспорядочного гомеостазиса, подобно тому, как популяция насекомых влияет на популяцию лягушек. Подобные явления можно наблюдать в стремлении мировых активов к безопасности. Если ставка по государственным бумагам повышается, они привлекают больше инвесторов. Затем повышаются цены на них, что опускает процентную ставку, и делает их менее привлекательными и т. д.
Странный аттрактор — самоорганизующий. Это место рождения свободы и понимания, как в действительности работает рынок. То, что поверхностный взгляд воспринимает как абсолютный хаос, к котором не заметно никакого порядка, имеет определенный порядок, базирующийся на странном аттракторе, когда наблюдение ведется из четвертого измерения.
Характеристикой странного аттрактора выступает чувствительность к начальным условиям, которая иногда называется «эффект бабочки». Малейшее отклонение от изначальных условий может привести к огромным 
различиям в результате.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1) Каковы причины появления синергетики и ее частных направлений?
2) Сформулируйте основные положения синергетики.
3) В чем различие системного и синергетического подходов к
исследованию сложных систем?
4) Дайте характеристику идей И. Пригожина, Н. Моисеева, Л. Курдюмова, Г. Хакена.
5) В чем различия и общность подходов идей различных школ?