Алгебраические фракталы.
3. Стохастические фракталы.
Геометрические фракталы.
Фракталы этого класса самые наглядные. В двумерном случае их получают с помощью некоторой ломаной (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры, получается геометрический фрактал.
Рассмотрим один из таких фрактальных объектов — триадную кривую Коха. Построение кривой начинается с отрезка единичной длины (рис. 3.1)- это нулевое поколение кривой Коха. Далее каждое звено (в нулевом поколении один отрезок) заменяется на образующий элемент, обозначенный на рисунке через п = 1. В результате такой замены получается следующее поколение кривой Коха.
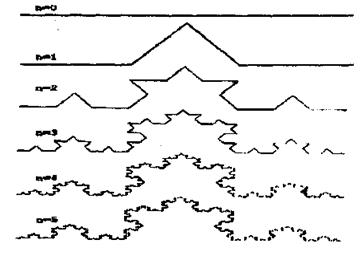
Рис. 3.1. Построение триодной кривой Коха
В 1-ом поколении — это кривая из четырех прямолинейных звеньев, каждое длиной по 1/3. Для получения 3-го поколения проделываются те же действия — каждое звено заменяется уменьшенным образующим элементом. Итак, для получения каждого последующего поколения все звенья предыдущего поколения необходимо заменить уменьшенным образующим элементом. Кривая n - го поколения при любом конечном n называется предфракталом. Нa рис. 3.1 представлены пять поколений кривой. При п, стремящемся к бесконечности, кривая Коха становится фрактальным объектом.
Для получения другого фрактального объема нужно изменить правила построения (рис. 3.2).

Рис. 3.2. Построение «дракона» Харпера — Хейтуэя
Алгебраические фракталы.
Это самая крупная группа фракталов. Получают их с помощью нелинейных процессов в n -мерных пространствах. Наиболее изучены двумерные процессы.
Если нелинейная динамическая система обладает несколькими устойчивыми состояниями, то каждое устойчивое состояние обладает некоторой областью начальных состояний, из которых система обязательно попадет в рассматриваемые конечные состояния. Таким образом, фазовое пространство системы разбивается на области притяжения аттракторов. Окрашивая области притяжения различными цветами, можно получить цветовой фазовый портрет этой системы (итерационного процесса). Меняя алгоритм выбора цвета, можно получить сложные фрактальные картины с причудливыми многоцветными узорами. Неожиданностью для математиков стала возможность с помощью примитивных алгоритмов порождать очень сложные нетривиальные структуры.
В качестве примера рассмотрим множество Мандельброта (рис. 3.3 и рис. 3.4).Алгоритм его построения достаточно прост и основан на простом итеративном выражении:
Z[i+1] =Z[i]xZ[i] + С,
 где Z[i] и С — комплексные переменные.
где Z[i] и С — комплексные переменные.
Рис. 3.3. Множество Мандельброта
Итерации выполняются для каждой стартовой точки С прямоугольной или квадратной области на комплексной плоскости.
Итерационный процесс продолжается до тех пор, пока Z[i] не выйдет за пределы окружности радиуса 2, центр которой лежит в точке (0,0), (это будет означать, что аттрактор динамической системы находится в бесконечности), или после достаточно большого числа итераций (например, 200 - 500) Z[i] сойдется к какой-нибудь точке окружности.

Рис. 3.4. Участок границы множества Мандельброта, увеличенный в 200раз
В зависимости от количества итераций, и течении которых Z[i] оставалась внутри окружности, можно установить цвет точки С (если Z[i] остается внутри окружности и течение достаточно большого количества итераций, итерационный процесс прекращается и эта точка растра окрашивается в черный цвет).
Описанный алгоритм дает приближение к так называемому множеству Мандельброта. Множеству Мандельброта принадлежат точки, которые в течение бесконечного числа итераций не уходят в бесконечность (точки, имеющие черный цвет). Точки, принадлежащие границе множества (именно там возникают сложные структуры), уходят в бесконечность за конечное число терапий, а точки, лежащие за пределами множества, уходят к бесконечность через несколько итераций (белый фон).