Наиболее общее представление процесса принятия решений

- Ядро бинарных отношений

Учить тетрадь

15. Групповое принятие решений. Методы большинства. Правило Кондорсе. Правило Борда. Медиана группового профиля. Выбор на основе средних рангов и медианы рангов.

Групповое принятие решений

Понятие ранжировки.

N = {1..n} количество участников процесса принятия решений

n- множество оцениваемых альтернатив

Ri, I ={1….n} ранжировки 1 индивидуума

Понятие группового профиля.

Набор ранжировок (R1…. Rn), выражающих мнения членов группы, определяет групповой профиль

Функция группового выбора

Функция F: Rn(A)->R(A)

Где R(A) является совокупностью всех возможных ранжировок, задающей правило получения групповой ранжировки.

ПРАВИЛО БОЛЬШИНСТВА

• Простое большинство

• Правило абсолютного большинства

• Правило голосования «большинство без худшего»

ПРАВИЛО КОНДОРСЕ

Для А и Б рассчитываются предпочтения А и Б Sab Sba

A > B if S ab> Sba

ПРАВИЛО БОРДА

Для А рассчитываются b(A)

A > B if b(A) > b(B)

Число Борда – количество менее предпочтительных альтернатив

Формальные методы подведения итогов:

- метод средних рангов

-метод медианы рангов

Медианы рангов

К примеру у 1 оценки 1 3 3 4 медиана 3

Метод средних рангов сумму рангов делим на количество получаем итоговый ранг

Медиана группового профиля

Медианой R группового профиля (R1… Rn) называется такая ранжировка, для которой сумма d(Rс волной,R1) +…. d(R,Rn) минимальна

Сигма ri rj(a,b) = 0 если предпочтения для a и b не совпадают

2, если одной ранжировке a>b, а в другой b>a

1, если в одной ранжировке a>b b>a, а в другой они равноценны

Тогда d(Ri;Rj) равно сумме всех значений по всем неупорядоченным

16. Метод нестрогого ранжирования для парных сравнений.

17. Понятия эффективности решения (оптимальность по Парето и Слейтеру). Пространство исходов и пространство критериев. Угол предпочтения. Конус предпочтения.

a. Методы отыскания множеств эффективных и слабо эффективных решений в дискретном и непрерывном случаях. Изменение статуса альтернатив при включении и удалении критериев.

18. Сетевые модели. Сетевые графики. Постановка задачи выбора варианта наилучшего распределения работ в сети по ресурсам.

Сетевой график – это графическое изображение процессов, выполнение которых необходимо для достижения поставленной цели.

19. Сведение многокритериальной задачи к однокритериальной: направления решений.

20. Методы формирования интегрального критерия (аддитивное, мультипликативное и иерархическое представление).

21. Виды зависимостей между показателями: зависимость значений (функциональная и статистическая зависимость), зависимость оптимальных значений, зависимость по предпочтению.

22. Основные методы нормировки локальных критериев.

Проблема нормализации локальных критериев возникает во всех задачах векторной оптимизации, когда локальные критерии имеют различные единицы измерения (килограммы, метры, секунды, рубли и т.д.) Исключение составляет лишь метод относительной уступки в котором нормализация осуществляется автоматически. В основу нормализации положено понятие «идеального вектора» т. е. вектора с идеальными значениями локальных критериев

.

В нормализованном пространстве критериев вместо действительного значения локального критерия y_i рассматривается безразмерная величина

.

В том случае, если лучшим считается большее значение критерия и если то .

Успешное решение проблемы нормализации во многом определяется тем, насколько удачным окажется выбор параметров идеального вектора. Рассмотрим три основных способа задания идеального вектора.

1-й способ. Идеальный вектор определяется некоторыми заданными значениями локальных критериев. Эти заданные значения может определить, например, заказчик разработки. Формальная запись:

.

Недостаток этого способа - полнейший субъективизм выбора.

2-й способ. Идеальным считается вектор, параметрами которого являются максимально возможные значения локальных критериев

.

3-й способ. В качестве параметров идеального вектора принимается максимально возможный разброс значений соответствующих локальных критериев, т.е.

23. Процедуры нахождения весовых коэффициентов важности: простое проставление весов, процедуры SMART и SWING, парное сравнение.

Метод анализа иерархий Т. Саати (МАИ).

1. попарное сравнение критериев

2. попарное сравнение альтернатив

3. вычисление собственных векторов-оценок предпочтения альтернатив по определенным критериям

4. вычисление собственных векторов-оценок важности критериев

5. расчет показателей качества альтернатив

6. упрощенный вариант метода анализа иерархий

a. Упрощенный вариант метода анализа иерархии В.Д. Ногина.

24. Лексикографический принцип поиска решения многокритериальных задач. Лексикографическое отношение предпочтения.

25. Метод ведущего критерия.

26. Метод «смещенного» идеала.

27. Метод последовательных уступок.

Ограничения типа «равенство» и «неравенство» задают слишком сильное различие между основным и дополнительными критериями (рис. 8). Меньшее различие дает метод уступок. Он реализуется следующим алгоритмом:

1. Частные критерии упорядочиваются в порядке убывания их важности.
2. Находится наилучшая альтернатива по наиболее важному критерию (на рис. 8 это , если самый важный критерий и , если им является ).

Определяется уступка – величина, на которую возможно уменьшить достигнутое значение самого важного критерия, чтобы за счет нее увеличить, насколько возможно, значение следующего по важности критерия и т.д. (на рис. 8 полученные таким образом альтернативы изображены точками и ).

28. Семейство методов ELECTRE.

В методе "ЭЛЕКТРА" разработана процедура многокритериального выбора наиболее предпочтительных объектов, включающая следующие этапы.

1. Для каждого из критериев вводится дискретная шкала возможных значений этого критерия, весовые коэффициенты критериев.

2. Для каждого из критериев строится граф, вершинами которого являются отдельные объекты множества, а дуги указывают на отношение доминирования между объектами в соответствии с данным критерием.

3. С учетом важности критериев и предпочтительности объектов вычисляются матрицы значений специальных коэффициентов, называемых индексами согласия и несогласия.

4. Для каждой пары объектов (x,y)Є X считается установленным отношение превосходства, скажем х над у, если значение соответствующего индекса согласия больше некоторого порогового значения, а индекс несогласия - меньше соответствующего порогового значения.

5. Строится обобщенный граф превосходства, структура которого зависит от выбранных пороговых значений.

Цель применения методов ЭЛЕКТРА - сужение паретовского множества альтернатив. Делается это так. Для каждого из критериев (предполагается, что они - числовые) определяется по результатам опроса ЛПР «вес» - число, характеризующее важность соответствующего критерия. Во всех модификациях метода ЭЛЕКТРА делается попытка получения от ЛПР информации качественного характера об относительной важности критериев (высказывания типа «критерии 3 и 4 имеют одинаковую важность и рассматриваемые совместно имеют большую важность, чем критерий 1») и преобразования ее в количественную, числовую. Проблема здесь состоит в том, что сделать это можно в общем случае множеством способов.

Далее, для каждой пары сравниваемых альтернатив x=(x₁,.....,x_n) и y=(y₁,.......,y_n) (где n - число критериев, а для дальнейшего мы через I обозначим множество критериев, т.е. ½½I½½= n) выполняются такие действия. Множество I разбивается на 3 подмножества:

I⁺(x,y) - множество критериев, по которым х превосходит у: x>y.

I^- (x,y) - множество критериев, по которым у превосходит х: у>х.

I⁼(x,y) - множество критериев, по которым х и у имеют одинаковые оценки: у=х.

Определяется относительная важность P P P каждого из этих подмножеств:

(* Î{+, -,=})

P_i. - коэффицент относительной важности i -го критерия. Теперь мы готовы сформировать правило сравнения альтернатив х и у:

- в методе ЭЛЕКТРА-I оно таково:

, .

Всё рассмотренное до сих пор весьма традиционно, и содержит традиционную погрешность в логических рассуждениях: получается, что очень маленький выигрыш по одному критерию может компенсировать очень большой проигрыш по другому. Для того чтобы эту трудность (погрешность) исключить, в методе «Электра» пытаются НЕ сравнивать очень сильно различающиеся альтернативы. Они просто объявляются несравнимыми. Вводится так называемый «индекс несогласия»:

х и у несравнимы, если d_xy ³d,

где d_xy - расстояние между х и у определяется как max_içx_i - y_iç, a d - т.н. порог индекса несогласия. Теперь введённые нами раньше соотношения модифицируются так:

в ЭЛЕКТРА-I

.

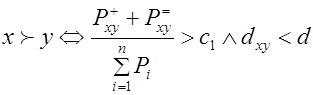Получаемое бинарное отношение, очевидно, уже не будет обладать свойством полноты. Это учитывается и в окончательном результате ЭЛЕКТРА. Он таков. В исходном паретовском множестве выделяется т.н. ядро, состоящее из недоминируемых по новому (описанному нами) бинарному отношению элементов и всех, несравнимых с ними (т.е. любой элемент, не вошедший в ядро, доминируется хотя бы одним элементом ядра). Отметим, что, к сожалению, нельзя гарантировать цикличность отношения, получаемого описанным способом.

29. Постановка задачи выбора в условиях полной неопределенности. Игры с Природой и модели выбора: Вальда (гарантированного результата), минимального сожаления Севиджа, оптимизма-пессимизма Гурвица.

30. Постановка задачи выбора в условиях риска. Критерии максимума ожидаемого среднего выигрыша и минимума ожидаемого среднего риска (Бернулли-Лапласа). Устойчивость выбора.

31. Использование дерева решений для выбора вариантов действий в условиях риска.