В последнее время всеобщее внимание сместилось на глобальную оптимизацию, как на средство разрешения кинематической избыточности. Nakamura иHanafusa[19]описывают этот подход и представляют алгоритм вычисления глобально оптимальных траекторий пространства сочленений для избыточных манипуляторов. В настоящем разделе мы представим альтернативную формулировку необходимых условий, опишем качественные особенности экстремальныхтраекторий и обсудим т еоретические основыпродолжения гомотопии [19] как подхода к построению алгоритма для этих вычислительно строгих (rigorous)задач.
Начнём с уравнения скорости (3). Наш подход состоит в том, чтобы сформулировать задачу нахождения траектории в пространствесочленений как задачу оптимизациис ограничениями, гденужно минимизировать интеграл пути:
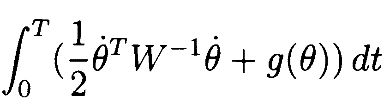(12)
с учётом кинематического ограничения x(t) = f(θ(t)). Вэтомкритериипредполагается, что матрица весов W симметрична иможетиметь явную зависимость от t.
Теорема 4.1 Траектории в пространстве сочленений, которые оптимизируют (12), удовлетворяют:
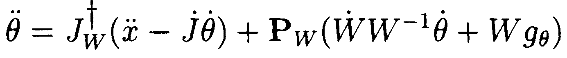(13)
где
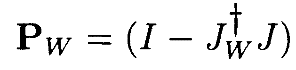
является взвешенным оператором проекции нуль-пространства Якобиана J, и
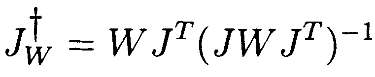
является взвешенным псевдо-обратным для J.
Доказательство. Эта теорема следует из вариационного аргумента, в котором вариациитраектории δθ в пространстве сочленений вынуждены лежать в направлении нуль-пространства J. Оператор Эйлера-Лагранжа, определённыйфункционалом (12), является
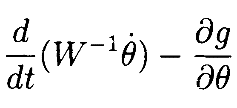
и, если θ(•) минимизирует (12) по всем траекториям, которые меняются относительно θ(•) в направлении kerJ(θ(t)), т.е. относительно всех траекторий, соответствующих данному пути x(•) в операционном пространстве, то θ(•) должен удовлетворять
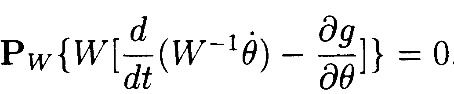(14)
Отметим, что Pw является ортогональной проекцией относительно скалярного произведения(innerproduct), определяемого симметричной положительно определенной матрицей W-1.
Если мы дифференцируем (1) дважды по t, мы получим
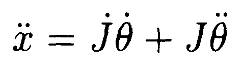
что можно эквивалентно записать, как
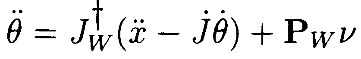(15)
для соответствующего выбора ν. Умножая обе стороны этого уравненияна оператор проекции Pw и отметив, что
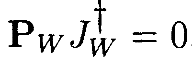
получим
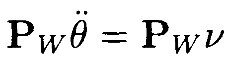
Используя (14), находим, что это подразумевает
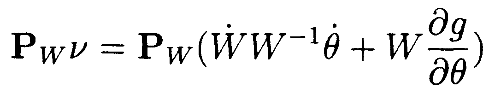
и подставляя это в (15), доказывает теорему. •
Чтобы однозначно указать оптимальное решение, необходимо рассмотреть граничные условия, а также необходимое условие, предоставляемое (13). Когда мы впервые начали изучать интегральные критерии для разрешения кинематической избыточности, мы надеялись, что, минимизировав интегральный критерий (12), найдем траектории в пространстве сочленений, которые удовлетворяют кинематическому ограничению (1), при этом оставаясь на расстоянии больше минимального от кинематических особенностей. К сожалению, как отмечалось в [18], решения (13) могут включать особые точки, если граничные условия выбираются достаточно злонамеренным (malicious) образом. В дальнейшем мы будем рассматривать случай периодическихграничных условий. Это естественно, поскольку рассматриваются периодические траектории операционного пространства. Таким образом, если x удовлетворяет x(0)=x(T),то цель – в том, чтобы найти траектории, которые удовлетворяют (13) с учётом θ(0)=θ(T) и θ˙(0)=θ˙(T).
Пример 4.1. Существование Кратных НегомотопическихЭкстремальных Решений.
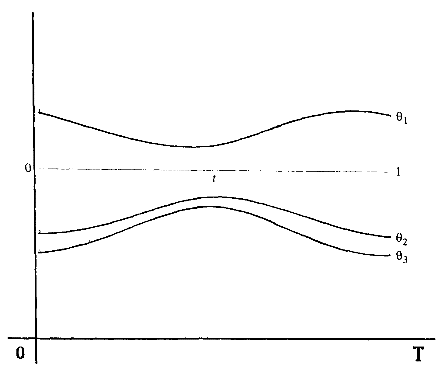
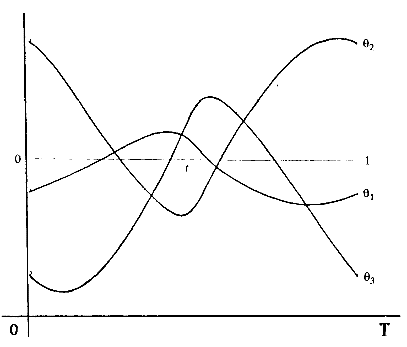
Оптимизация по траекториям с периодическими граничными условиями может быть применена к планированию путей манипулятора из Примера 1.2. Такая геометрия была специально выбрана для иллюстрации качественных различий оптимальных и неоптимальных траекторий, так их особенно просто наблюдатьпри сравнении. Необходимые условия, выраженные в терминах системы дифференциальных уравнений (13) вместе с периодическими граничными условиями, в общем случае будут достаточными для определения семейства траекторий, являющимися экстремумамиинтеграла по траектории (12). В рассматриваемом здесь конкретном примере мы выбрали g(θ)=0 и W(t)=I. На рисунке 5 показана геометрия плоского трёхзвенного манипулятора и траектория в операционном пространстве, которую он должен вывести. Захват манипулятора должен описать против часовой стрелкивыделенный кругза единицу времени. На рисунках 6 и 7 показана динамика изменения углов сочленений2х разных траекторий, удовлетворяющихуравнению (13) и являющихся периодическими. Траектория на рисунке 6 имеет гораздо меньшую стоимость (cost), чем на рисунке 7.
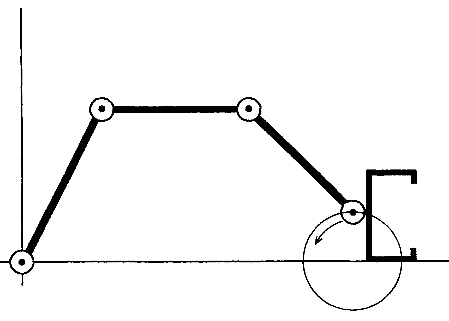
Рисунок 5: Плоский трёхзвенный манипулятор, выводящий окружность
| 
|
| Рисунок 6:Экстремальное решение A для необходимых условий | Рисунок 7:Экстремальное решение B для необходимых условий |
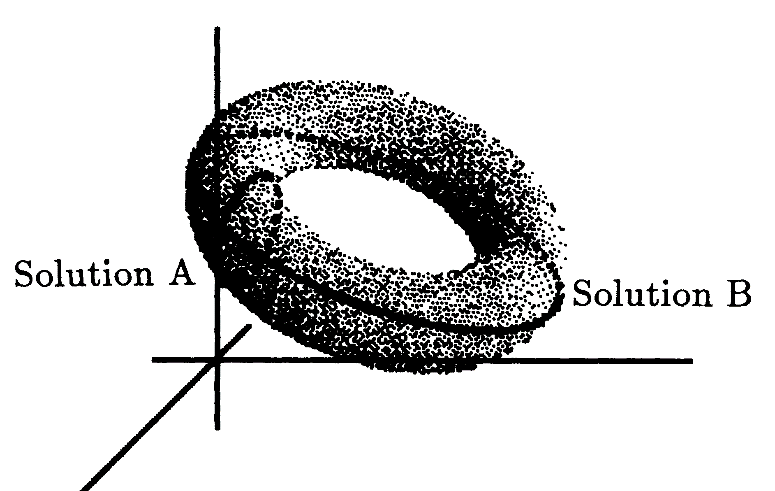
Рисунок 8: Траектории решений A и B нарисованы на поверхности { θ: f(θ)=x(t), 0≤t≤1 }
Чтобы лучше понять это поведение, на рисунке 8 показана взаимосвязь 2х траекторий, если рассматривать их как траектории в пространстве суставов. На этом рисунке мы видим трёхмерную визуализацию множества углов соединений, которые удовлетворяют кинематическому ограничению f(θ)=x(t) для некоторого t. Поскольку манипулятор имеет одну степень избыточности, размерностьмножества таких углов соединений на единицу больше, чем размерность набора x(t). В этом случае данная поверхность эквивалентна деформированному тору. Для фиксированного t набор θ -значений, соответствующих x(t), является замкнутой кривой, которая окружает деформированный тор по большему радиусу. Когда времяувеличитсяот 0 до 1, манипулятор будет выводить кривую, которая окружает тор вокруг малого радиуса, чтобы оставаться на желаемой траектории.
На рисунке показано, что траектория с более низкойстоимостью окружает тор по меньшему радиусу в точке, где совокупное расстояние, которое должно быть пройдено, (в пространстве сочленений)мало. Траектория с более высокой стоимостью обходит тор по малому радиусу единожды и, в то же время,ещё единождыобводит тор вокруг большего радиуса. Грубо говоря, манипулятор пересекает нуль-пространство 1 раз при выполнении движения. Важно отметить, что более длинная траектория не может непрерывно деформироваться в более короткую траекторию. Таким образом, мы пришли к решениям обратной задачи кинематики, которые находятся в различных гомотопических классах. Обе кривые являются локально оптимальными решениями в пределах своих гомотопических классов. Этот пример показывает, что алгоритмы, основанные только на необходимых уравнениях, не смогут различать решения в разных гомотопических классах без дальнейшего уточнения. Частично для решения этой проблемы, а также частично для решения проблемы поиска вычислительно эффективных методов решения краевых задач, связанных с глобальнымиметодами планирования путей, мы завершаем этот раздел отчётом о последних результатах применения методов продолжения гомотопии к задаче планирования пути.
Конкретная задача, которую рассмотрим, состоит в минимизации функционала стоимости
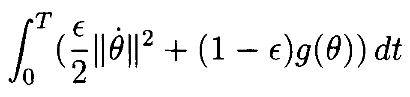(16)
с учётом ограничения (1) и периодических граничных условий
θ(0)=θ(T), θ˙(0)=θ˙(T). (17)
Предполагаем, что траектория операционного пространства x(•) замкнута (т.е. x(0)=x(T)), а функция g в подынтегральном выражении является дифференцируемой функциейконфигурации пространства сочленений (например, индекс манипулируемости изпредыдущего раздела). Для простоты предполагаемтакже, что степень избыточности n–m=1.
Уравнение (13) теперь принимает вид
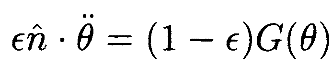(18)
где
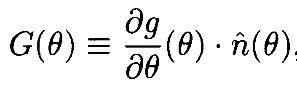(19)
и n̂(θ) – нормализованный вектор нуль-пространстваЯкобиана J(θ).
Параметргомотопии ϵ варьируется между 0 и 1, и когда ϵ=0, задача сводится к поиску экстремума интеграла от g(θ) с учётом ограничений. Нетрудно показать, что это эквивалентно поточечной оптимизации g с учётом ограничения (1) в каждой точке θ вдоль пути. Поскольку при ϵ=0 задачу планирования движения гораздо легче решить (используя, скажем, технику расширенного Якобиана), чем общую оптимизационную по траекториям задачу, хочется понять, могут ли решения задачи ϵ=0 фактически использоваться для того, чтобы инициировать гомотопическое продолжение. Отметим, что это потенциально трудный вопрос, поскольку характер задачи оптимизации (16) резко меняется при ϵà0. В пределе необходимые условия меняются от дифференциального уравнения второго порядка (18) к алгебраическому уравнению G(θ)=0, так что гомотопия включает особенное возмущение (singularperturbation).
Для более острой фокусировки на проблеме, ещё раз рассмотрим манипулятор из Примера 1.2 вместе с локальной критериальной функцией g(θ) = sin2θ2 + sin2θ3. На Примере 3.1 в случае 
=1 для j=1,2,3, мы приходим к ограничению G(θ) = θ2–θ3.
Методрасширенного Якобиана создаёттраекторию в пространстве сочленений, множество точек которой является подмножеством пересечения поверхностей { θ: G(θ)=0} и { θ: f(θ)=x(t), 0≤t≤T}. Для этого Примера и кривой операционного пространства из Примера 4.1 область обращенияв нользначений G (zerolocusG)пересекает поднятую (обратную) область кривойоперационного пространства(тор), изображенный на Рисунке 8 в виде кривых, которые окружают тор вокруг двух малых экваторов.Обратите внимание, что из двух экстремальных траекторий, которые мы нашли для задачи глобальной минимизации в Примере 4.1, только траектория с названием Решение А является гомотопной кривым, связанным с задачей локальной оптимизации. Решение В, находящееся в другом гомотопическом классе, очевидно, не может быть непрерывно деформировано в решение, заданное методом расширенногоЯкобиана с данной критериальной функцией.
На момент написания статьи активно исследуются условия, при которых решения θϵ(t) из (18)-(17) будут сходиться по разумной норме к θ0(t) –к решению алгебраического уравнения G(θ)=0. Хотя мы не можем сказать точно, но некоторые предположения о регулярности представляются существенными. Таким образом, будем предполагать, что в окрестности θ0(t) нет кинематических особенностей. Мы также предположим, для простоты, что степень избыточности равна 1, т.е. n=m+1. Тогда в окрестности кривой θ0(t) существует непрерывно определенный единичный вектор n̂(θ) в нуль-пространстве J, и можно доказать следующий результат.
Теорема 4.2 (Martin, [17]) Дана бесконечно-дифференцируемая локальнаякритериальная функция g(θ), предположим, что θ0(t) является строгим локальным минимумом g с учётом кинематического ограничения f(θ(t))=x(t) для данной замкнутой бесконечно-дифференцируемой кривой х(t) в операционном пространстве. Предположим также, что в окрестности θ0(t) нет кинематических особенностей. Тогда существуют ϵ1>0 и семейство решений θε(t) для (18)-(17) такое, что для 0<ϵ<ϵ1,
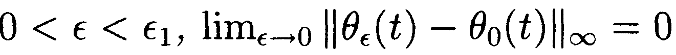
Доказательство этой теоремы будет проведено с помощью последовательности лемм.
Будет удобно переписать (18) вместе с кинематическим ограничением (1) как одномерную неавтономнуюзадачу, выразив уравнение (18) через локальные координаты на многообразии
f-1(x(•)), (точные условия, при которых обратный к f образ траектории операционного пространства фактическиявляется многообразием, описаны в [17]) Отметим, что, поскольку предполагаем, что θ0(t) является подъёмом (lifting) гладкого пути [20] x(t) в операционномпространстве, имеющего ненулевой тангенсв каждой точке, отсюда следует, что θ0(t) имеет поперечное пересечение (transverseintersection) в каждой точке с векторным полем n̂(θ0(t))
нуль-пространства. На Рисунке 9 показана такая кривая θ0 на примере многообразия Рисунка 8. В окрестности (vicinity) θ0(t) обозначим через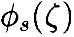 
поток векторного поля n̂ с начальным условием:
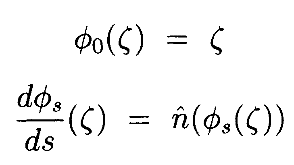
На Рисунке 9 изображён такой поток, начинаяс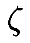 
на кривой θ0. Этот поток на самом деле является траекторией нуль-пространства, соответствующей конкретной точке в операционном пространстве. Так как n̂ – нормализованный относительно некоторой нормы в пространстве сочленений, переменная s – это расстояние, пройденноевдоль траектории нуль-пространства, чтобы достичь точки 
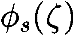.Определим θ(s,t)≡φs(θ0(t)). Так как θ0 является поперечной (transverse) к n̂, и по предположению в окрестности θ0(•) нет кинематических особенностей, пара (s,t) определяет набор локальных координат на многообразии ограничений (constraintmanifold), как показано на Рисунке 10.
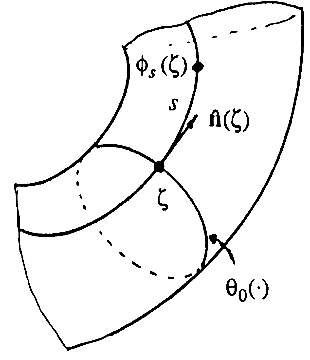
Рисунок 9: Кривая θ0(•) и поток n̂.
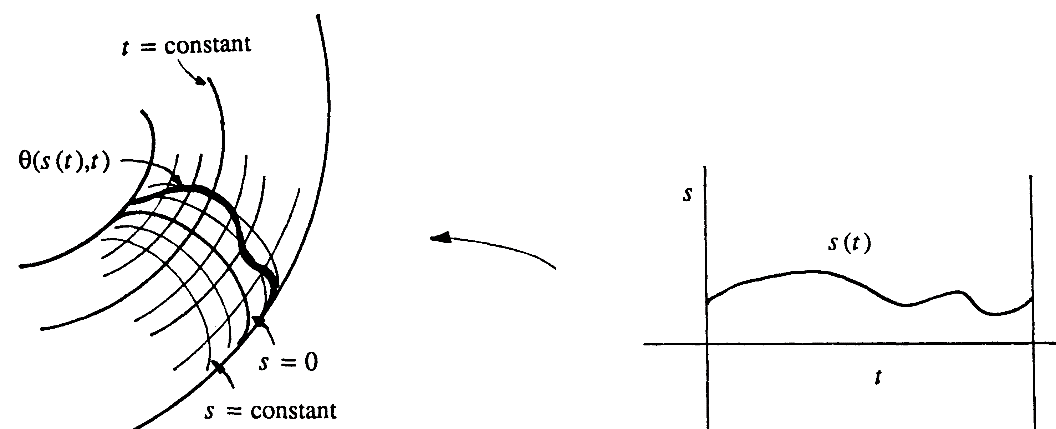
Рисунок 10: (s,t) -координаты, определенные с помощью θ0(•) и потока n̂
на многообразии ограничений.
Переписывая уравнение (18) в координатах (s,t), мы эффективно удаляем ограничение из (18). Сначала вычислим n̂ (θ)⋅ θ˙˙ в координатах (s,t). Согласно условию теоремы, в рассматриваемых величинах достаточно гладкости, чтобы написать
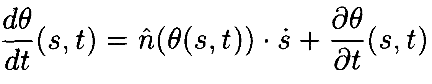
и
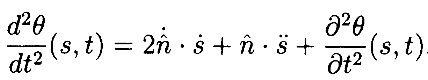
где
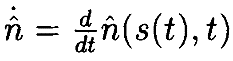
Таким образом
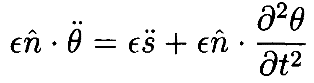
где мы использовали тот факт, что n̂ является единичным вектором, так что n̂ ⋅ n̂=1 и n̂ ⋅ n̂˙=0. Следовательно, можно переписать (18) как
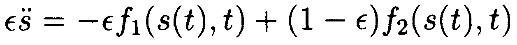
где
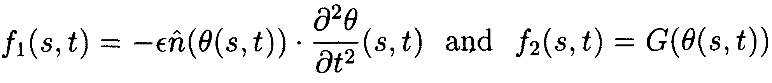
Поскольку нас интересует случай, когда ϵ приближается к нулю, будет удобно заменить ϵ на ϵ2/(1+ϵ2), что позволяет переписать приведённое выше уравнение как
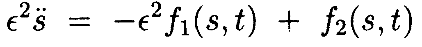(20)
Если выбрать θ0(t) как кривую, которая минимизирует g(θ(t)) при каждом t, на который распространяется кинематическое ограничение, то из Теоремы 2.3 следует, что G(θ0(t))≡0. Непосредственный аргумент дополнительно показывает, что
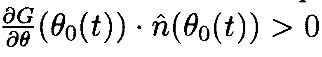
Это означает, что при s=0 элемент f2 такой, что
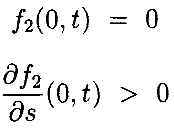
В этой измененной форме (recastform) рассматриваемая задача состоит в том, чтобы определить обстоятельства, при которых решения для (20) существуют, и сходятся в соответствующем смысле к θ0 при ϵà0.
Замечание 4.1. Наше обсуждение будет отличаться от того, что можно найти в стандартных источниках (например, [24]), в том, что первый по порядку вариант решения задачи второго порядка, описанный выше, не удовлетворяет техническим условиям, обычно налагаемым на лидирующий член (leadingterm) в асимптотическом разложении Якобиана (asymptoticexpansion). Эти условия исключают точки поворота (turningpoints), требующиеся, чтобычастичная в правой части уравнения относительно s˙ была отделена от нуля. В рассматриваемом случае эта частичная (thispartial) равна нулю во всей области t.
Замечание 4.2. В неравенствах, которые будут изложены в следующих Леммах, все нормы на функции считаются равномерными нормами, если не указано иное.
Лемма 4.1. Предположим, что a(t), b(t) дважды дифференцируемы и периодичны с периодом T>0 на [0,T], причём a(t)>0. Тогда существует ϵ1>0 такая, что для каждой 0<ϵ<ϵ1 дифференциальное уравнение
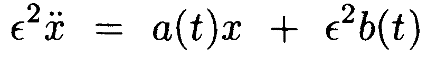
имеет решение x(t), периодическое с периодом T и такое, что ||x||< ϵ2D||b|| и ||x˙||< ϵB||b|| для некоторых B, D>0. Здесь || • || является равномернойнормой [21].
Доказательство: Мы " в первую очередь " рассмотрим систему
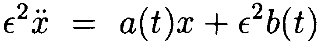
чтобыполучить, при ϵ>0 векторную систему уравнений
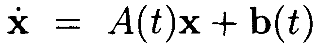
где
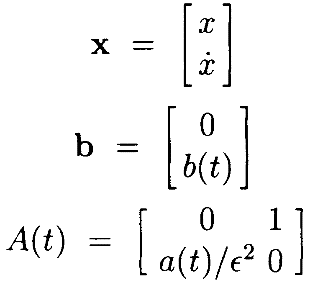
Диагонализируем (diagonalize) A(t) в каждый момент времени путём замены переменных
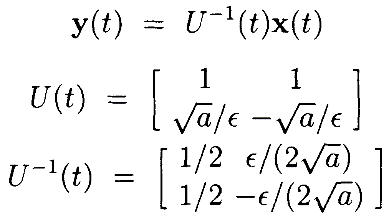
Дифференциальное уравнение затем приобретает вид
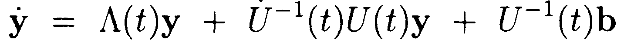
где
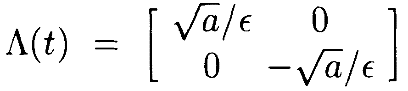
Далее, используя формулу замены переменных, соответствующую периодическим граничным условиям этой задачи:
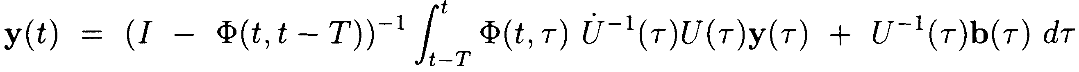
где
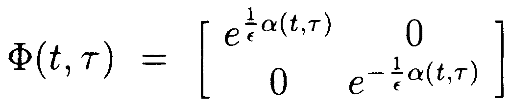
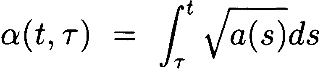
Мы ожидаем из теории Флоке [22]и того факта, что Φ – диагональная, что Φ(t,t-T) не зависит от t. Если мы определим
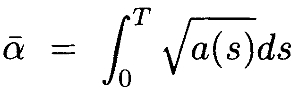
То мы видим, что
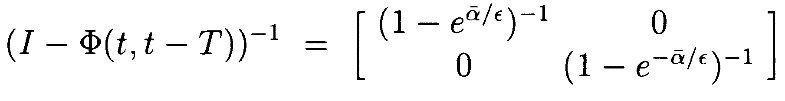
Отметив, что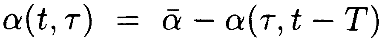 
,видим, что
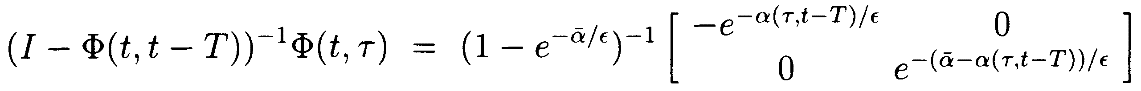
Если мы определим величину выше, как Ψ(τ,t–T), тоформулас изменёнными параметрами станет
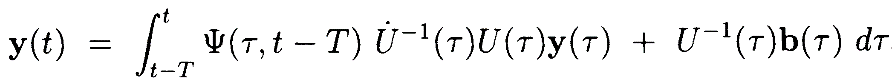
Отметим, что Ψ(τ,t–T) остаётся ограниченной при t–T<τ<t, когда мы варьируем ϵ>0, в отличие от Φ(t,τ).
Чтобы получить границы для x, поменяем переменные обратно на x = Uy
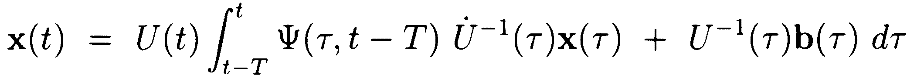
Далее рассмотрим 2 члена в этом интеграле. Если определить
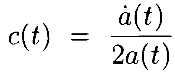
то имеем
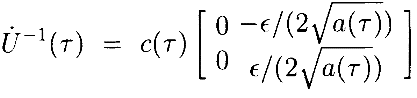
Вычислим
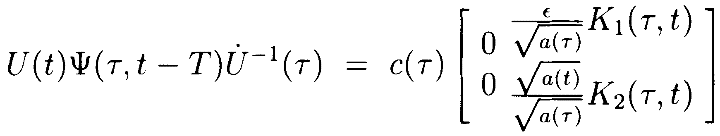и
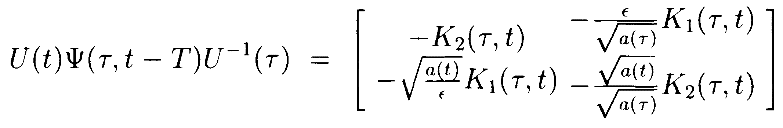
где
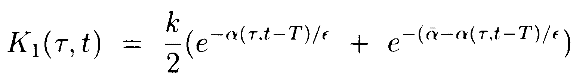
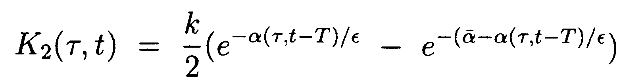
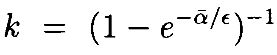
При этом можно написать интегральное уравнение как
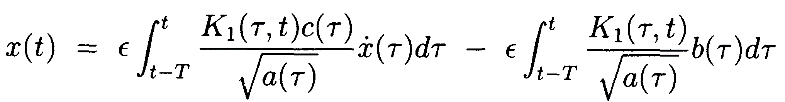
и
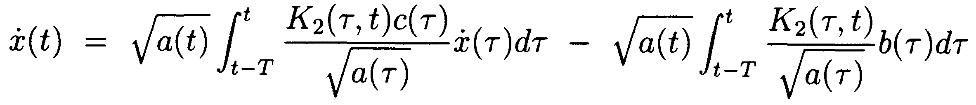
или, собирая элементы в виде
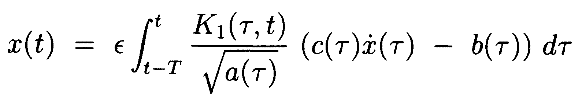
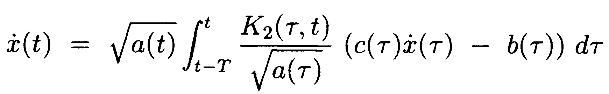
Запишем эти 2 интегральных уравнения в терминах операторов F1 и F2:
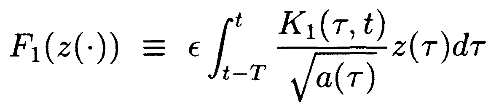
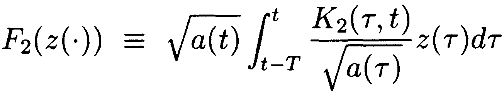
Интегральныеуравнения могутбытьзаписаны
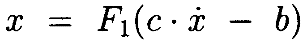
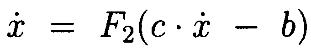
Чтобы продемонстрировать, что решение этих уравнений существует, продолжаем, как обычно, показывать, что решение является пределом последовательности функций, полученных из итерации Пикара [23]. Отметим, что решение второго уравнения является достаточным, поскольку решение первого определяется из него 1 интегрированием. Определим
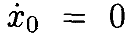
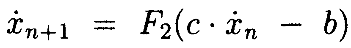
Видим, что
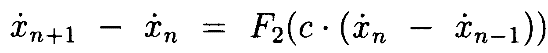
Далее мы хотим получить ограниченияна интегралы выше.
Поскольку предположили, что a(t)>0, функция α(τ,t–T), появляющаяся в Ki(τ,t), монотонно возрастает и поэтому имеет обратную функцию, которую обозначим как τ(α):
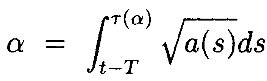
Таким образом, можнозаменить переменную интегрирования на α вместе с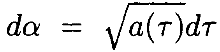 
:
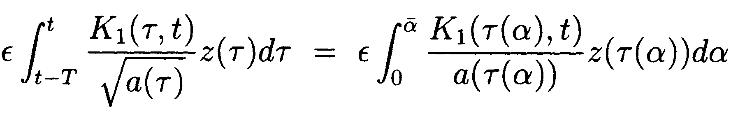
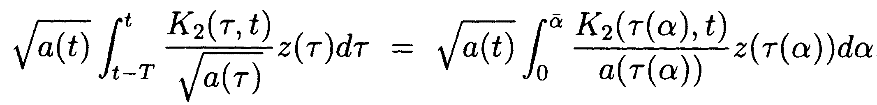
Используя равномерную норму,
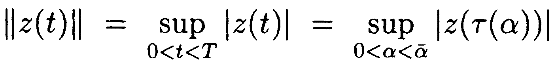
можноограничить интегральные уравнения как
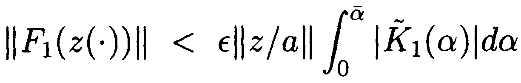
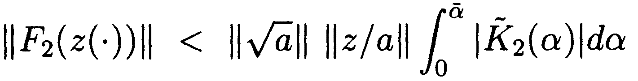
где
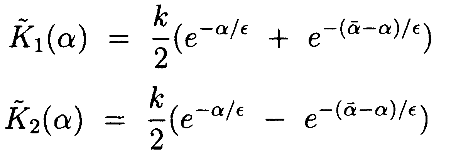
Так как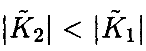 
и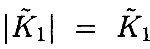 
для каждой α, можноограничитьвышеупомянутые интегралы
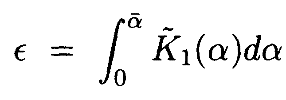
Тогда отграничения интегральных операторов
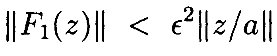
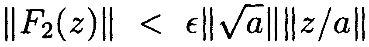
Мывидимзатем, что
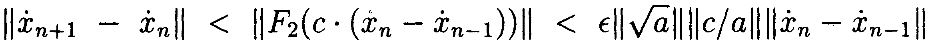
или
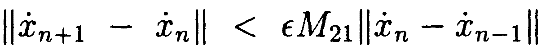
где M21 – это функция только от a и её производных, она ограниченанашими гипотезами на a. Видно, что последовательность xn˙ является последовательностью Коши (Cauchysequence) для ϵ < ϵ0, ϵ0=M21-1. Последовательность сходится к предельной точке, поскольку множество непрерывных периодических функций Cp0[0,T] является полным (complete) по равномерной норме. Последовательность xn, таким образом, сходится.
Это подразумевает, что х˙ и, следовательно, x, удовлетворяющие дифференциальному уравнению для 0<ϵ<ϵ0, существуют. Далее хотим найти границы для этих решений. Определим
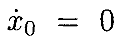
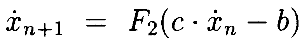
Применяя приведенные выше ограниченияпоследовательности, видим, что
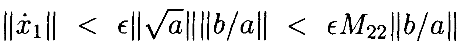
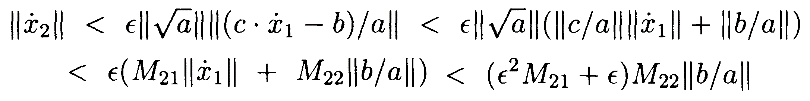
Продолжая в том же духе,
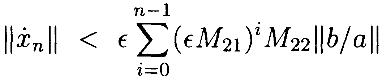
Это ограничение на xn˙ сходится к
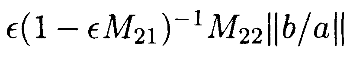
Оно подразумевает, что можно выбрать B и ϵ1 такими, что
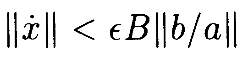
для всех ϵ<ϵ1. Имеем схожие ограничения на ||x||, как
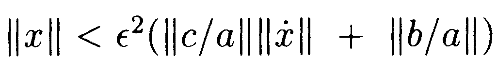
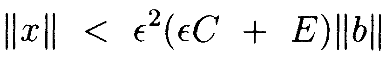
Наконец, берём D равное ϵ1C+E, что доказывает лемму. •
Далее немного расширим приведённую выше Лемму, чтобы включить в неё возмущение ϵ2 для a(t). Для простоты докажем элементарное расширение Леммы 4.1 с использованием варианта итерации Пикара, который будет использоваться для обработки нелинейного случая.
Лемма 4.2. Предположим, что a0(t), a1(t) и b(t) дважды дифференцируемы и периодичны с периодом T>0. Если a0(t)>0, то дифференциальное уравнение
,
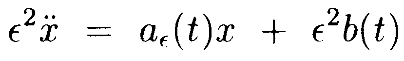где aϵ(t) = a0(t) + ϵ2a1(t), имеет периодическое решение x(t) для 0<ϵ<ϵ1 такое, что ||x||<ϵ2D||b|| и ||x˙||<ϵB||b|| для действительных чисел B, D>0.
Доказательство: Рассмотрим следующую последовательность дифференциальных уравнений:
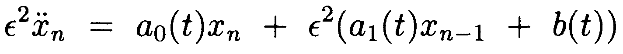
где x0≡0. Сначала рассмотрим разности
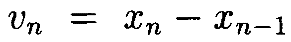
Они удовлетворяют
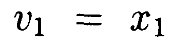
и
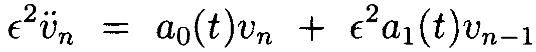
Это уравнение имеет решение v n, показанное в Лемме 4.1, что для B и D
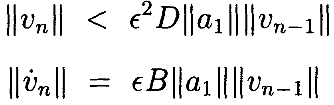
Видно, что длядостаточно малой ϵ, и
Как и в Лемме 4.1, это означает, что xn сходятся к дифференцируемой функции. Далее найдутся ограничения xn: если рассмотреть
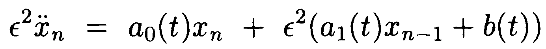
можно использовать ограничения Леммы 4.1 для получения
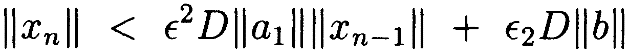
и
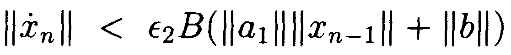
Как и в доказательстве Леммы 4.1, 1я последовательность неравенств ограничена сверху геометрическим рядом:
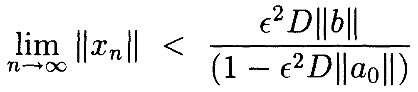
Для достаточно малой ϵ это даёт ограничение
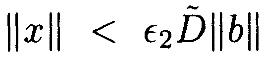
Использую этот факт во второй серии,получаем
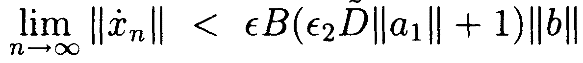
Опять же, для достаточно малого эпсилона можнонаписать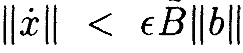 
.•
Лемма 4.3. Заданы aϵ(t), как в Лемме 4.2, и b(t) дваждыдифференцируемая и периодическая функция периода T, дифференциальное уравнение
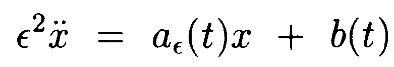
имеет периодическое решение x(t) для каждого 0<ϵ<ϵ1 такого, что ||x||* < K||b||*, где K>0 и
||•||* является нормой:
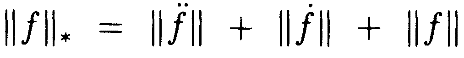
Доказательство:Сначала поместим дифференциальное уравнение в форму, подходящую для применения Леммы 4.2. Определим
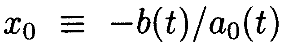и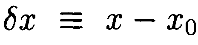 
Это приводит уравнение в форму
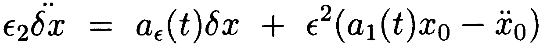
Мывычисляем
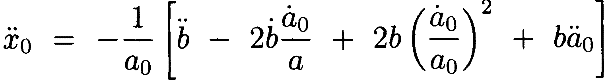
Отсюда видно, что
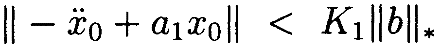
для некоторого K1, зависящего только от a0(t) и её производных. Из этого дифференциального уравнения следует, мы можем ограничить δx˙˙
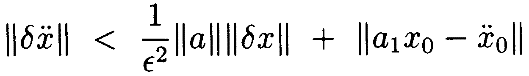
где δx=x–x0 играет роль неизвестной переменной, как и в доказательстве Леммы 4.1.
Из ограничений, указанных в Лемме 1, имеем
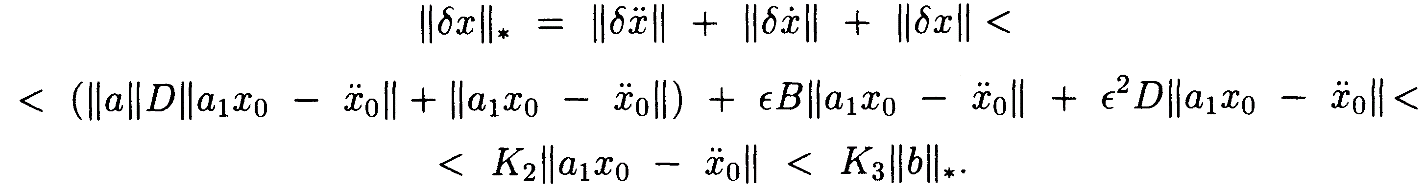
В силу неравенства треугольника
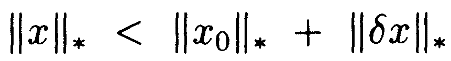
Так как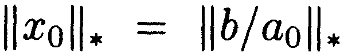 
имеем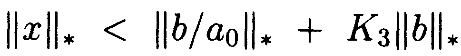 
или, наконец, 
.•
Лемма 4.4. Предположим, g(x,t) – такая, что для всех 0<t<T
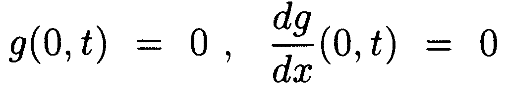
иболеетого, длянекоторого η>0 ивсех |x|<η следующее ограниченно (равномерно
????пропуск в книге полстраницы…
Доказательство: Запишем разность g(x1,t)—g(x2,t) как
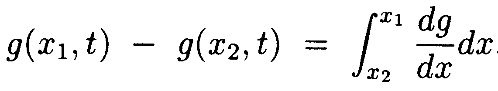
Определив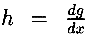 
и заменив переменную интегрирования на s, где 
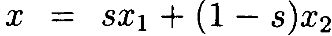, разность становится
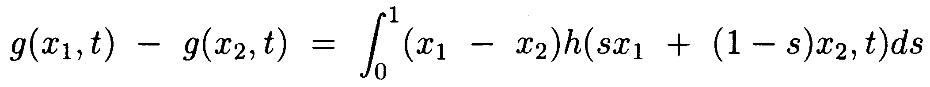
Если положить M0=sup0<s,t<1h(sx1 + (1–s)x2, t), то
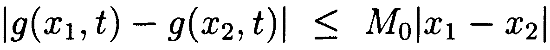
Далеерассмотрим 1ю производную:
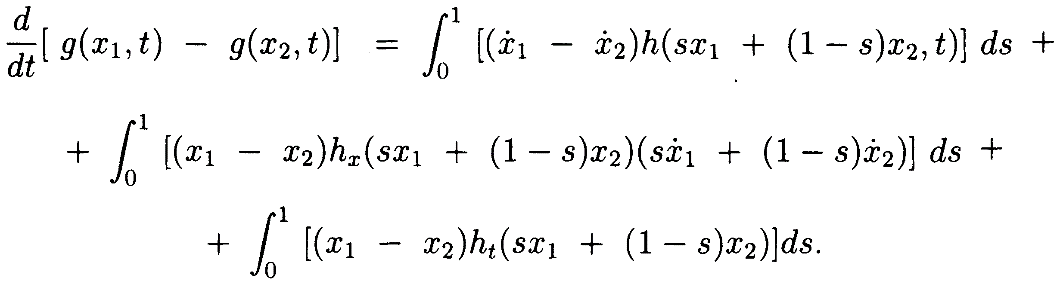
Еслиопределим
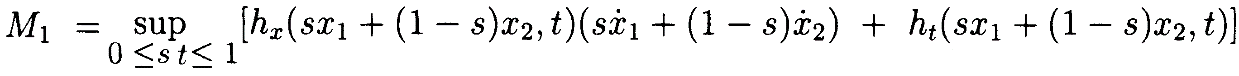
товидно, что
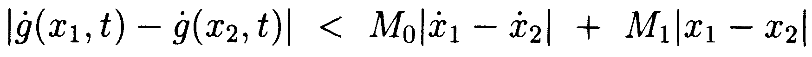
Далеевычисляя 2ю производную:
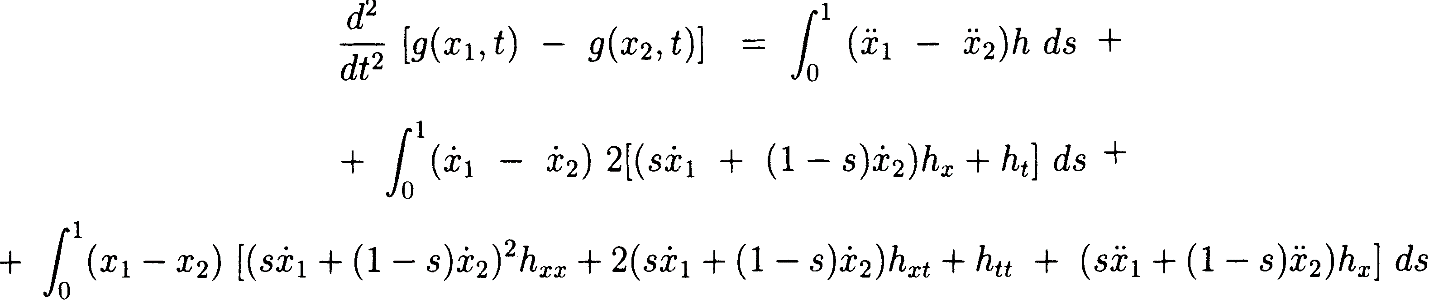
где мы пропустили аргумент для h и его производных. Определяя
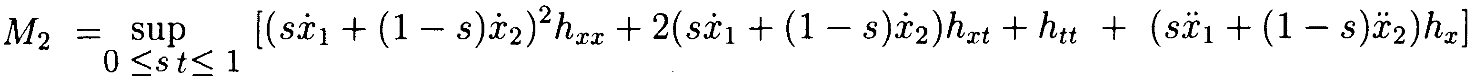
видим, что
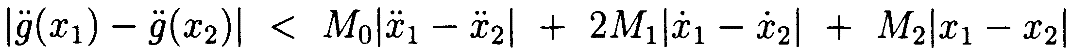
Это даёт
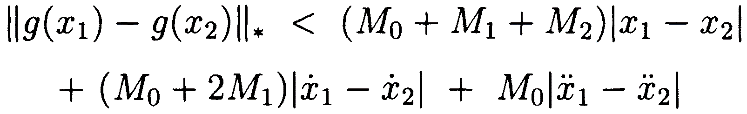
Если ||x1||* и ||x2||* меньше, чем δ, можно ограничить значениями M0, M1 и M2. Что даёт
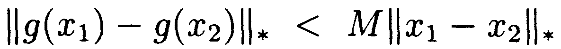
для некоторого конечного M. Далее, M стремится к 0 как и ||x1||*, и ||x2||*, поскольку M0, M1 и M2 все обращаются в ноль вместе с ||x1||* и ||x2||*. •
Теорема 4.3. Пусть f1(x,t) и f2(x,t) являются 4 раза дифференцируемыми, периодичны по t, с f2(0,t)=0.
Далее, предположим, что ||f1(0,t)||*<∞ и
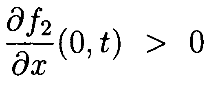
При этих предположениях уравнение
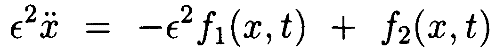
имеет периодические решения xϵ для 0<ϵ<ϵ1, где xϵà0 равномерно при ϵà0.
Доказательство: Разложим дифференциальное уравнение около x≡0. Дифференциальное уравнение становится
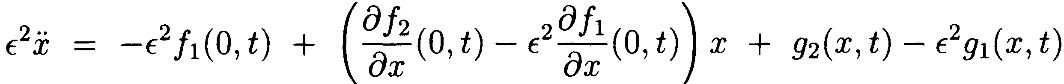
Самые правые члены – это остатки разложений f2 и –ϵ2f1 первого порядка около x≡0. Если установить gϵ(x,t)=g2(x,t)–ϵ2g1(x,t),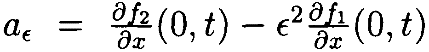 
и b(t)=f1(0,t), имеем дифференциальное уравнение в виде
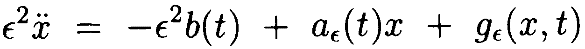
Теперь используя Лемму 4.2 и Лемму 4.3, а также вариант итерации Пикара, покажем существованиерешения.
Во-первых, ограничим диапазон ϵ так, чтобы aϵ>0. Выберем ϵ1 так, что 0<ϵ<ϵ1 подразумевало бы aϵ(t)>0 для всех t.
Определим последовательность функций un с помощью рекурсии
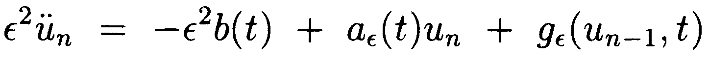
где u0≡0. Позже потребуем, чтобы все ||un||* были бы меньше δ>0. Установим по индукции:предположим, что решение un–1 существует. Затем используя Лемму 4.3, где выражение
–ϵ2b(t)+gϵ(un–1,t) играет роль b(t) в этой лемме, покажем, что
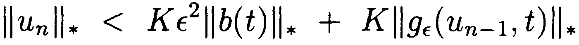
Если ||un–1||*<δ, можем использовать Лемму 4.4 для ограничения правого члена:
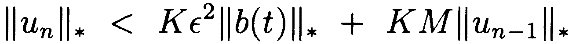
Поскольку Mà0 при δà0, то можно найти δ достаточно малую, чтобы из ||un–1||* <δ вытекало, что KM<½. В то же время можно найти ϵ2<ϵ1 достаточно маленькую, чтобы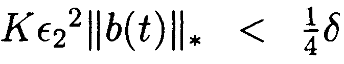 
Таким образом, когда ϵ<ϵ2 и ||un–1||* <δ, имеем
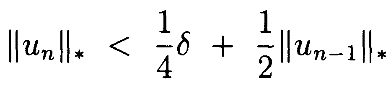
Это также означает, что ||un||* <δ также. Поскольку u0=0, имеем ||u1||* <¼δ. Следовательно, когда ϵ<ϵ2, ||un||* <δ для всех n по индукции. Тем самым, выбрав ϵ2, можно гарантировать, что все un будут малы. Фактически, приведенная выше последовательность является геометрической последовательностью (geometricsequence), ограниченной
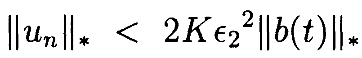
Теперь, хотя мы показали, что значения un ограничены, должны ещё показать, что они сходятся. Рассмотрим разности v n=un–un-1. Эти v n должны удовлетворять
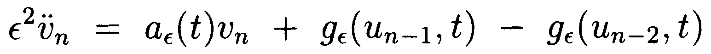
По Лемме 4.3 приведённое выше уравнение имеет решения v n, где
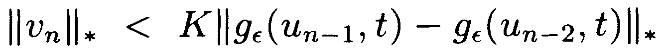
Мы снова можем применить Лемму 4.4, чтобы ограничить крайний правый член:
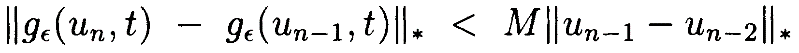
так что
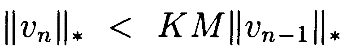
Чтобы показать сходимость, установим условия, при которых KM<1. Напомним, что в Лемме 3Mà0 также, каки ||un||*, и ||un–1||*. Таким образом, существует некоторая δ>0 такая, что из неравенства ||un||* <δ для всех n следует, что KM<1. Поскольку мы показали, что можем выбрать ϵ2 такое, что ||un||* <δ для всех n существует некоторое ϵ2>0 такое, что MK<1.
Тем самым устанавливает, что un является последовательностью Коши (Cauchysequence) по норме ||•||*. Поскольку пространство дважды дифференцируемых функций является полным по этой норме, un сходятся к дважды дифференцируемой функции, которая является решениемдифференциального уравнения
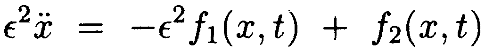
Так как
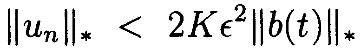
имеем
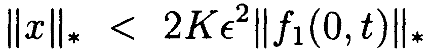
для 0<ϵ<ϵ2. Таким образом, решение уравнения теоремы x(t) стремится к 0 равномерно при ϵà0. •
ДоказательствоТеорем