Ранний подход к разрешению кинематической избыточности в манипуляторах по заданному пути в оперативном пространстве x˙(t) состоял в том, чтобы решить (3) для скорости сочленений θ˙ минимальной нормы || θ˙ ||. Эта идеяпредложенав 1969г.Whitney[23], имела 2 привлекательные черты. Сначала казалось разумным надеяться, что путём минимизации || θ˙ || в каждый момент времени кинематические особенности будут автоматически исключаться, и, во-вторых, потому что можно записать решение, минимизирующее норму, вявном виде θ˙=J+x˙, где J+=JT(JJT)-1 - обобщённыйобратный Якобиан Moore-Penrose, алгоритмы планирования могут быть реализованы рекурсивно с использованием стандартных численных методов для обыкновенных дифференциальных уравнений. К сожалению, более тщательный анализ обобщённого обратного подхода Мура-Пенроуза к планированию движения для кинематически избыточных манипуляторов выявил несколько изначально непредвиденных проблем. Следующая теорема показывает, что этот подход не генерирует траектории пространства сочленений, которые позволяют избежать кинематических особенностей в практическом смысле.
Теорема 2.2 (Baillieul). Рассмотрим манипулятор, конфигурации пространства сочленений и операционного пространства которого связаны, как (1). Пусть e>0 и θS – точка, в которой J=J(θ) имеет неполный ранг (т.е. θS определяет кинематически особенную конфигурацию), и пусть θ * – точка, такая что || θ*–θS || <e. Наконец, пусть x*=f(θ*). Тогда для любой конфигурации рабочего пространства x0 и любой C1-кривой x(•), начинающейся в x0 и заканчивающейся в x*, существует кривая θ (•), соответствующая x(•), как
θ˙ = J+x˙ (5),
которая заканчивается в θ*.
Доказательство. Предположим, что e, θS, θ *, x0, x* и кривая x(•) удовлетворяют условию этой теоремы. При повторной параметризации, если необходимо, мы можем принять x(0)=x0 и x(1)=x*, и определить обратную траекторию в рабочем пространстве с помощью y(t)=x(1-t) для 0<t<1 и определите траекторию θ (•) в пространстве сочленений с помощью дифф. уравнения
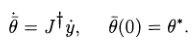
Тогда легко проверить, что кривая θ(t)=θ(1-t) удовлетворяет заключению теоремы. •
Другая практическая проблема с подхода обобщённого обратного решения Мура-Пенроуза была указана Klein и Huang [14]. Их моделирование показало, что замкнутые траектории в операционном пространстве не всегда приводят к замкнутым траекториям в конфигурационном пространстве. Это свойство вызывает озабоченность, посколькусуществует неопределенность в отношении того, как соединения робота будут конфигурироваться после нескольких повторных циклов выполнения задач. Топологические проблемы, связанные с привязкой замкнутых путей в пространстве сочленений к замкнутым путям в операционном пространстве, рассмотрены в [5]. В [21] показано, что неинтегрируемая связь между путями в оперативном пространстве и путями в пространстве сочленений может интерпретироваться в терминах неинволютивности[14] некоторого распределения векторных полей. Эта проблема повторяемости была решена в 1985 г. [1] расширеннымметодом Якоби, подробности которого будут приведены в следующем разделе.
2.2 Поточечные (pointwise) Критерии Оптимизации и Функциональные Ограничения для разрешения Кинематической Избыточности.
Завершаем этот раздел обсуждением роли оптимизации в различных подходах к разрешению кинематической избыточности. В литературе было предложено множество критериев кинематической оптимальности, включая минимизацию скорости в пространстве сочленений, избеганиепрепятствий по максимально возможнойвеличинепо отношению к различным мерам расстояния, избегание пределов сочленений и избегание кинематических особенностей. (см. [20])
Кинематически особенные конфигурации определяются стремящимся к нулю det(JJT), а
критерииизбеганияособенностей по максимально возможному краю включают в себя
· минимизацию g1(θ) = tr((JJT)-1) (Baillieul, [2]),
· максимизацию g2(θ) = λmin(JJT) (=наименьшее собственное значение JJT, Klein, [13]),
· максимизацию g3(θ) = sqrt(det(JJT)) индекса манипулятивности (Yoshikawa, [25]).
Если дана кинематическая функция f, то согласно следующей теореме любой критерий оптимальности g этого вида определяет «поверхность оптимальности », которая эффективно разрешает избыточность.
Теорема 2.3 (Baillieul, [1]) Необходимое условие для того, чтобы θ0 определяла локальный максимум целевой функции (objectivefunction) g(θ) с учётом ограниченияпозиции f(θ) = x, состоит в том, что
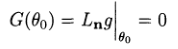
для всех векторов n из ноль-пространств а J(θ), где Lng обозначает производную Ли [15] (Lie) функции g по направлению вектора n.
Доказательство. Предположим, что θ0 является локальным максимумом g(θ), где θ ограничено нахождением в слое (fiber) {θ: f(θ) = x} при фиксированном x. Назовём кривые в этом слое «самодвижениями »и отметим в первую очередь, что самодвижения начинаются из θ0 и направлены в ноль-пространство J(θ0). Вывод теоремы следует из наблюдения, что если θ0 определяет локальный максимум в слое, то изменение первого порядка в g при любом самодвижении через θ0 должно быть равно нулю. •
Важность критериев оптимальности для функционального ограничения движений избыточных механизмов (и, следовательно, устранения избыточности) не полностью раскрывается в этой теореме. Использование ограничений, которые не возникают в связи с какой-либо формой оптимизации, могут блокировать движение механизма, приводя к значительному реальному уменьшению объёма рабочего пространства. Читатель, возможно, пожелает построить примеры этого явления.
По ряду причин желательно понимать, как определять критерии оптимальности, не прибегая к координатам. Необходимость в без-координатных определениях хорошо понимается геометрами и может быть просто понята в настоящем контексте следующим образом:предположим, что положение захвата манипулятора задается с точки зрения настройки угловсоединений как
x = f(θ),
где x – это m - вектор, а θ – как n>m - вектор. Избыточность может быть разрешена путём ограничения переменных сочленений m -мерной поверхностью. Предположим, что такая поверхность имеет локальную параметризацию вида θ=θ(u), где u∈Rm. Тогда вышеуказанная позиционная связьлокально задаётся так
x = G(u),
где G(u)=f(θ(u)). Тогда можно определить ограниченный аналог упомянутоговыше
индекса манипулируемости g3(θ), записав
g(u) = (det[(JuG)(JuG)T])1/2
где JuG = ∂G/∂u, легко видеть, что он зависит от выбранной параметризации θ=θ(u). Этот подходне обеспечивает содержательного измерения степени ограничения движения, ограничивая переменные сочленениябыть наданной поверхности. Следующая теорема будет полезна для устранения этой нежелательной зависимости от координат.
Теорема 2.4 Приведенные выше критерии эквивалентны следующему:
,
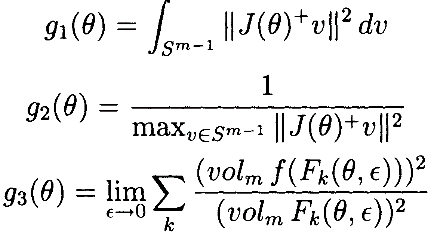где Fk(θ,ε) – это k -й m -мерный срез (параллельный k -й координатной m -плоскости) через стандартное n -куб с линейной размерностью ε, центрированный в θ, и volm обозначает m -размерный объём. Сумма здесь берётся по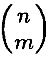 
стандартным координатным m -плоскостей в Rn.
Sm-1 обозначает единичную m-1 - сферу в Rm.
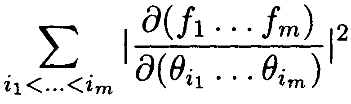Читателю предлагается выработать доказательство этой теоремы самостоятельно. Случай g3 доказан в [2]. Важное наблюдение, сделанное в [2], заключается в том, что det(JJT) = сумме квадратов mxm миноров J. Т.е.
det (JJT) = (6)
Каждый член в сумме является квадратом определителя Якобиана некоторого отображения. Таким образом, как следует из теоремы, его можно рассматривать как определённое отношение m -мерных объёмов, заметённых (sweptout) в операционном пространстве, к соответствующим объёмам в пространстве сочленений. Эта точка зрения оказывается ключевой в расширении определения индекса манипулируемост и в ситуациях, когда конфигурации суставов манипулятора ограничены гиперповерхностью G(θ)=0. Чтобы сделать это расширение, мы должны быть в состоянии вычислить индекс манипулятивности относительно координат поверхности.
Предположим, что в окрестности некоторой точки на поверхности мы можем решить G(θ)=0 и записать θn=θn(θ1,…,θn-1). В этой окрестности функцию кинематики f следует рассматривать, как функцию от n-1 переменных:
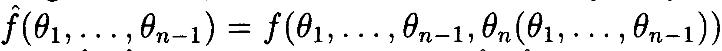
Каждый член в сумме (6) не заменяется на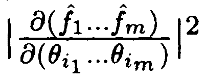 
,а скорее на
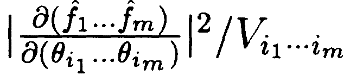
где Vi1…im – квадрат элемента m -мерного объёма на поверхности:
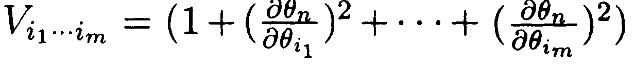
Теперь можно показать, что
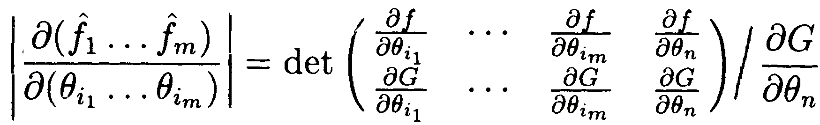
Отсюда
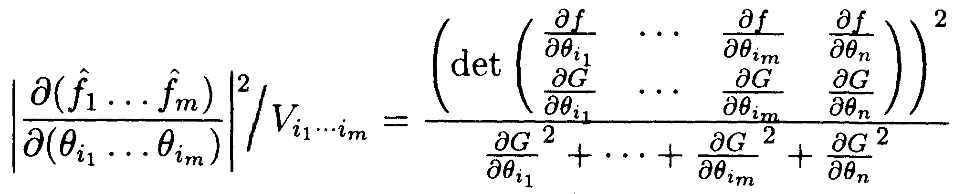
Расчёт предполагает, что мы могли бы определить индекс ограниченной манипулируемостифункции кинематики f относительно функции ограничений G путём суммирования членов данного вида, такой подход будет чётко отражать важную роль, которую сыграла координата θn в приведенном выше расчёте. В общем случае вышеупомянутый расчёт может повторяться для каждой координаты θk, и результаты могут быть усреднены для получения желаемой величиныинварианта (invariantquantity).
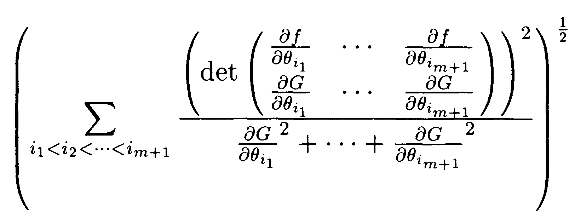Определение 2.1. Рассмотрим кинематически избыточный манипулятор, имеющий кинематическую функцию f с размером пространства сочленений n и размером сокращённого операционного пространства m. Индекс ограниченной манипулируемости (constrainedmanipulatabilityindex), связанный с f, и ограничение G(θ)=0 задаётся как
mG(θ) =
Детального исследования практической пользы этого индекса не будет (см. [2]), за исключением определения этой величины при изучении иерархий ограничений. В следующем разделе будет отмечено, что алгоритмические особенности, связанные с методом расширенного Якобиана, лежат в области обращениязначений (zerolocus)[16] индекса ограниченной управляемости в ноль.
Замечание 2.1. В специальном случае при n=m+1, индексом ограниченной манипулируемости записывается
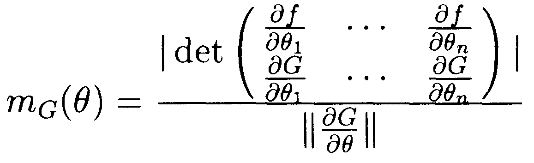(7)
В этом случае индекс ограниченной манипулируемости может быть интерпретирован в терминах метрики Римана [17], индуцированной (inducedonsurface) на поверхности G(θ)=0 с помощью естественной римановой метрикой окружающего неограниченного пространства сочленений. Обратите внимание, что для каждого θ такого, что G(θ)=0,
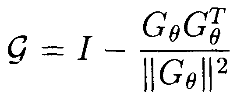
является ортогональной проекцией на пространство касательных (tangentspace) к поверхности G(θ)=0 в точке θ (Gθ обозначает вектор-столбец частной производной ∂G/∂θj, j=1,...,n, вычисленной в точке θ). 
симметрична и, если θ(t) определяет дифференцируемую кривую на G(θ)=0, то ||θ˙(t)||2 = θ˙(t)T θ˙(t). Следовательно, nxn -матрица определяетунаследованный метрический тензор Римана относительно θ -координат на поверхности G(θ)=0. Простой аргумент, использующий свойства определителей, показывает, что mG(θ) в (7) можно переписать как
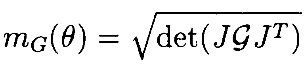
Это можно считать стандартным индексом манипулируемости для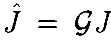 
, Якобиан спроецированна касательное пространство для G(θ)=0. Заметим, что при n>m+1 наше более общее определение mG(•) не имеет такой простой интерпретации.
В дополнение к кинематическим критериям оптимальности, которые мы обсудили, ряд авторов проводил оптимизацию динамических и кинетических величин для разрешения движения кинематически избыточных манипуляторов. Hollerbachи Suh([12]), например, изучали движения, траектории которых предназначены для поддержания требований к крутящему моменту (torque) для всех приводов сочленений в заданных диапазонах. К сожалению, моделирование ([12]) показало, что такое основанное на крутящем моменте разрешение избыточности может привести к непредвиденным и резко нестабильным движениям. Проблема состоит в том, что все локально оптимальные методы устранения избыточности игнорируют будущее и оптимизируют критерии в каждый момент времени, таким образом могут выбирать бедственные действияс глобальной точки зрения. Мы видели пример локальной оптимизации, приводящей к плохим глобальным характеристикам, выше, где показали, что минимизация скорости в каждый момент не будет генерировать траектории в пространстве сочленений, обходящие кинематические особенности. Maciejewski([16]) обсуждал подобные патологии, возникающие в движениях, основанных на локальнойминимизации крутящего момента.
3. Локальные Методы Решения Кинематической Избыточности: Метод Расширенного Якобиана
Локальные методы генерации траекторий в пространстве сочленений θ(•), соответствующих заданным траекториям в операционном пространстве x(•), имеют 2 преимущества: они просты в реализации и способны адаптироваться к непредвиденным изменениям x(•). В этом разделе мы введём метод расширенного Якобиана, первоначально предложенный в [1]. Этот метод отвечает требованию повторяемости и естественновключает критерии кинематической оптимальности типа, представленного в последнем разделе. Недавняя работа Shamirи Yomdin([21]) показывает, что это по сути единственныйвоспроизводимый локальный метод.
Придобавлении целевой функции g для оптимизации при выполнении движения, обратите внимание, что из Теоремы 2.3 следует, что будет n–m ограничений Gj(θ)=0, j=1,…,n-m, где Gj(θ)=Lng – производная Ли от g в j -м независимом направлении в нуль-пространстве [18] Якобиана. Если захват роботаследует траектории x(t), вдоль которой соответствующая конфигурация сочленений θ(t) является в каждой точке экстремумом g, то имеем
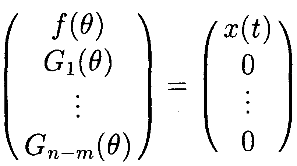
Дифференцирование обеих сторон обеспечивает (прямую) кинематическую зависимость между угловыми скоростями сочленений и скоростью захвата робота:
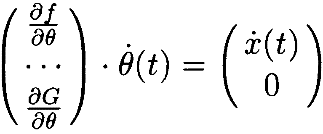(8)
Матрица коэффициентов
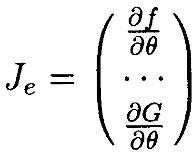
является квадратной, будем называть её расширенным Якобианом.
При условии, что расширенный Якобиан является неособым (non-singular) вдоль интересующей траектории, мы можем решить обратную задачу кинематики, написав
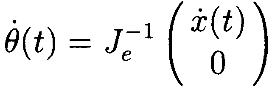
Очевидно, что расширенный Якобиан будет особенным (singular) в любой точке, где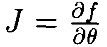 
имеет особенность. Другиеособыеточки расширенногоЯкобиана характеризуютсяследующим.
Теорема 3.1 (Baillieul, [3]) Предположим, что θ0 – это конфигурация в пространстве сочленений, в которой J имеет полный ранг m. Je – особенный тогда и только тогда, когда линейный оператор, определенный (n-m)xn -матрицей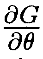 
, ограниченной нуль-пространством J, имеет ранг <n–m.
Доказательство. Предположим, что Je имеет особенность. Если rank[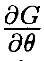 
(θ0)]<(n–m),то
rank(Je)<(n–m) тем более (afortiori) когда он ограничен подпространством kerJ.
Если Je(θ) имеет особенность, но оба J и 
имеют полный ранг, то существует вектор-строка v≠0 такая, что v ⋅ Je(θ0)=0, и v имеет ненулевые компоненты vi при i≤m, а также ненулевые компоненты vi при i>m. Но тогда подразумевается, что существует (n-m) - набор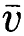 
≠0 такой, что ⋅ 
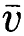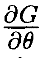(θ0) лежит в пространстве строк матрицы J(θ0). Тогда 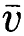⋅ 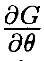(θ0) ⋅ n̂=0 для всех n̂∈kerJ(θ0) и, следовательно,
rank[ 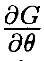(θ0)]<(n–m) на kerJ(θ0).
Предположим, с другой стороны, что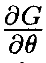 
(θ0) имеет ранг <n–m на kerJ(θ0). Пусть N будет
(n-m)xn -матрица, строки которой охватывают kerJ(θ0). Мы можем написать
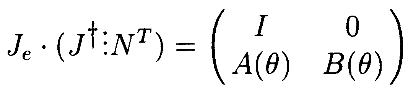(9)
и т.к. B(θ0)=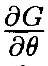 
(θ0) ⋅ NT имеет ранг <n–m и ранг Je=m+rankB(θ0), то, следовательно, Je(θ0) с особенностью, что и доказывает теорему. •
Baillieulи ко. [4] показали, что любая C1- траектория пространства сочленений, не проходящая через особенность J, может быть порождена подходящим выбором v (•) в
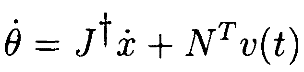(10)
Проблема задания v (•) некоторым полезным способом может быть решена с помощью метода расширенного Якобиана. Умножая обе части (9) на составной вектор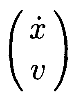 
, из (9) и (10)получим:
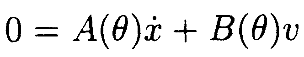(11)
Если Je – обратимый, видно, что B(θ) имеет ранг =n–m. В этом случае всегда можно найти v.
Если Je – необратимый, всё ещёвозможно найти v, который решает уравнение (11), но с более деликатными условиями.
Определение 3.1. Точки в пространстве сочленений, где (11) не может быть решена для некоторого значения x˙, называются алгоритмическими особенностями, связанными с ограничениями:
G1(θ)=0,...,Gn-m(θ)=0
Важно подчеркнуть, что алгоритмические особенности не являются дефектами, полученными методом расширенного Якобиана. К сожалению, они неизбежно вводятся, если функциональные ограничения (или критерии оптимальности) используются для устранения избыточности практически в любом манипуляторе, имеющем вращательные соединения (revolutejoints).
Пример 3.1. Предположим, что критерием оптимальности является индекс манипулятивности
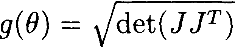, рассмотренный в предыдущем разделе. Рассмотрим(избыточный) плоскийманипулятор из Примера 1.2. Положение его захвата относительно основания определяется выражением
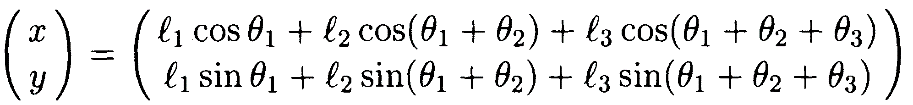
Максимизация индексаманипулятивности для этой кинематической функции эквивалентна максимизации g(θ)=sin2θ2+sin2θ3. Это определяет ограничение G(θ)=Lgn̂=0, в терминах которого определяется расширенный Якобиан (когда l j=1 для j=1,2,3, это ограничение просто θ2—θ3=0). Как отмечено в [1], алгоритмические особенности для этого критерия возникают, когда захват касается основания, образуя замкнутую кинематическую цепь, не допускающуюникаких движений в переменных суставов θ2 и θ3. Эти алгоритмические особенности также могут быть интерпретированы в терминах индекса ограниченной манипулятивности Раздела 2
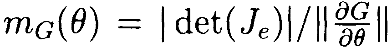
Если l j=1 для j=1,2,3, то
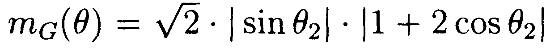
Установив это значение равным нулю, находим, что особенности, связанные с критерием, возникают, когда sinθ2=0 (являются особенностями J), а когда θ2=±2π/3, являются алгоритмическими особенностями, связанными с ограничением.