Задание 11 № 35
Дана арифметическая прогрессия:  Найдите сумму первых десяти её членов.
Найдите сумму первых десяти её членов.
Решение.
Определим разность арифметической прогрессии:

Сумма первых k -ых членов может быть найдена по формуле

Необходимо найти  , имеем:
, имеем:

Ответ: 50.
Задание 11 № 113
Дана арифметическая прогрессия  Найдите
Найдите  .
.
Решение.
Определим разность арифметической прогрессии:

Член арифметической прогрессии с номером  может быть найден по формуле
может быть найден по формуле

Необходимо найти  , имеем:
, имеем:

Ответ: 23.
Задание 11 № 165
Дана арифметическая прогрессия  Найдите сумму первых десяти её членов.
Найдите сумму первых десяти её членов.
Решение.
Определим разность арифметической прогрессии  :
:

Сумма первых k -ых членов может быть найден по формуле
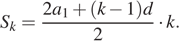
Нам необходимо найти  , поэтому в формулу для нахождения
, поэтому в формулу для нахождения  ставим 10 вместо
ставим 10 вместо  :
:

Ответ: 75.
Задание 11 № 137301
Выписаны первые несколько членов арифметической прогрессии: 3; 6; 9; 12;… Какое из следующих чисел есть среди членов этой прогрессии?
| 1) 83 | 2) 95 | 3) 100 | 4) 102 |
Решение.
Найдем разность арифметической прогрессии:  Зная разность и член арифметической прогрессии, решим уравнение относительно n, подставив данные в формулу для нахождения n -го члена:
Зная разность и член арифметической прогрессии, решим уравнение относительно n, подставив данные в формулу для нахождения n -го члена:

Членом прогрессии является число 102. Таким образом, правильный ответ указан под номером 4.
Ответ: 4.
Примечание.
Заданная арифметическая прогрессия состоит из чисел, кратных трём. Числа 83, 95 и 100 не кратны 3, они не являются членами прогрессии; а число 102 кратно 3, оно является её членом.
Задание 11 № 137302
Арифметические прогрессии  ,
,  и
и  заданы формулами n-го члена:
заданы формулами n-го члена:  ,
,  ,
, 
Укажите те из них, у которых разность  равна 4.
равна 4.
1)  и и 
| 2)  и и 
| 3)  , ,  и и 
| 4) 
|
Решение.
Найдем 

Для каждой из прогрессий  ,
,  и
и 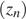 найдем разность:
найдем разность:
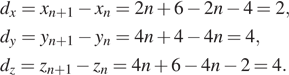
Разность прогрессии равна 4 для прогрессии  и
и 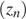 . Таким образом, верный ответ указан под номером 2.
. Таким образом, верный ответ указан под номером 2.
Ответ: 2.
Задание 11 № 137303
В первом ряду кинозала 30 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в ряду с номером n?
1) 
| 2) 
| 3) 
| 4) 
|
Решение.
Количество мест в рядах кинозала образуют арифметическую прогрессию. По формуле для нахождения n -го члена арифметической прогрессии имеем:

Таким образом, правильный ответ указан под номером 1.
Ответ: 1.
Задание 11 № 137304
Дана арифметическая прогрессия: 33; 25; 17; … Найдите первый отрицательный член этой прогрессии.
1) 
| 2) 
| 3) 
| 4) 
|
Решение.
Для члена  имеем:
имеем:  По формуле нахождения n -го члена арифметической прогрессии имеем:
По формуле нахождения n -го члена арифметической прогрессии имеем:

Первое число, которое удовлетворяет этому условию, число 6. Следовательно, первым отрицательным членом прогрессии является 
Таким образом, правильный ответ указан под номером 1.
Ответ: 1.
Задание 11 № 137305
Арифметическая прогрессия задана условиями:  ,
,  . Какое из данных чисел является членом этой прогрессии?
. Какое из данных чисел является членом этой прогрессии?
| 1) 80 | 2) 56 | 3) 48 | 4) 32 |
Решение.
Найдем разность арифметической прогрессии: 
Зная разность и первый член арифметической прогрессии, решим уравнение относительно  , подставив данные в формулу для нахождения n -го члена:
, подставив данные в формулу для нахождения n -го члена:

Таким образом, число 48 является членом прогрессии. Правильный ответ указан под номером 3.
Ответ: 3.
Задание 11 № 311254
Найдите сумму всех отрицательных членов арифметической прогрессии: −8,6; −8,4;...
Решение.
1. Найдём разность прогрессии:  .
.
2. Найдём число отрицательных членов прогрессии.
Составим формулу  -го члена:
-го члена:  .
.
Решим неравенство  получим
получим  < 44. Значит,
< 44. Значит,  = 43.
= 43.
3. 
Ответ: −189,2.
Задание 11 № 311330
Арифметическая прогрессия 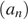 задана формулой n-го члена
задана формулой n-го члена  и известно, что
и известно, что  . Найдите пятый член этой прогрессии.
. Найдите пятый член этой прогрессии.
Решение.
Найдём разность прогрессии: 
Тогда для пятого члена прогрессии 
Ответ: 11.
Задание 11 № 311363
В арифметической прогрессии  известно, что
известно, что  . Найдите четвёртый член этой прогрессии.
. Найдите четвёртый член этой прогрессии.
Решение.
Имеем: 
Ответ: 7.
Задание 11 № 311909
Арифметическая прогрессия задана условиями: 
 . Найдите сумму первых 19 её членов.
. Найдите сумму первых 19 её членов.
Решение.
Сумма n первых членов арифметической прогрессии даётся формулой

По условию, 
 откуда получаем
откуда получаем

Ответ: 95.
Задание 11 № 314399
Какое наибольшее число последовательных натуральных чисел, начиная с 1, можно сложить, чтобы получившаяся сумма была меньше 528?
Решение.
Для ответа на вопрос задачи требуется найти такое наибольшее  что
что  Рассмотрим арифметическую прогрессию с первым членом
Рассмотрим арифметическую прогрессию с первым членом  и разностью
и разностью  Cумма
Cумма  первых членов арифметической прогрессии вычисляется по формуле:
первых членов арифметической прогрессии вычисляется по формуле:

в нашем случае

Найдем наибольшее натуральное решение неравенства  . Для этого найдём корни уравнения
. Для этого найдём корни уравнения

Вычислим дискриминант:

откуда получаем:

Таким образом, при  сумма 32 слагаемых равна 528. Следовательно, наибольшее натуральное число, для которого сумма будет меньше 528, равно 31.
сумма 32 слагаемых равна 528. Следовательно, наибольшее натуральное число, для которого сумма будет меньше 528, равно 31.
Ответ: 31.
Примечание.
Можно заметить, что  откуда сразу же получаем:
откуда сразу же получаем:  или
или 
Задание 11 № 314408
Найдите сумму всех положительных членов арифметической прогрессии 11,2; 10,8; …
Решение.
Определим разность прогрессии:

Найдём выражение для n -го члена прогрессии:

.
Найдем номер последнего положительного члена прогрессии:

Следовательно, чтобы найти сумму всех положительных членов данной арифметической прогрессии необходимо сложить её первые 28 членов.
Сумма n первых членов арифметической прогрессии даётся формулой
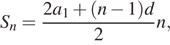
откуда имеем:

Ответ: 162,4.
Задание 11 № 314423
Какое наименьшее число последовательных натуральных чисел, начиная с 1, нужно сложить, чтобы получившаяся сумма была больше 465?
Решение.
Для ответа на вопрос задачи требуется найти такое наименьшее  что
что 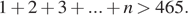 Рассмотрим арифметическую прогрессию с первым членом
Рассмотрим арифметическую прогрессию с первым членом  и разностью
и разностью  Cумма
Cумма  первых членов арифметической прогрессии вычисляется по формуле:
первых членов арифметической прогрессии вычисляется по формуле:

в нашем случае

Найдем наименьшее натуральное решение неравенства  . Для этого найдём корни уравнения
. Для этого найдём корни уравнения

Вычислим дискриминант:

откуда получаем:

Таким образом, при  сумма 30 слагаемых равна 465. Следовательно, наименьшее натуральное число, для которого сумма будет больше 465, равно 31.
сумма 30 слагаемых равна 465. Следовательно, наименьшее натуральное число, для которого сумма будет больше 465, равно 31.
Ответ: 31.
Примечание.
Можно заметить, что  откуда сразу же получаем:
откуда сразу же получаем:  или
или 
Задание 11 № 314425
Найдите сумму всех отрицательных членов арифметической прогрессии –7,2; –6,9; …
Решение.
Определим разность прогрессии:

Найдём выражение для n -го члена прогрессии:

.
Найдем номер последнего отрицательного члена прогрессии:
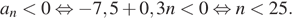
Следовательно, чтобы найти сумму всех отрицательных членов данной арифметической прогрессии необходимо сложить её первые 24 члена.
Сумма n первых членов арифметической прогрессии даётся формулой

откуда имеем:

Ответ: −90.
Задание 11 № 314619
Арифметическая прогрессия (an) задана условиями: a 1 = 3, an + 1 = an + 4. Найдите a 10.
Решение.
Определим разность арифметической прогрессии:

Член арифметической прогрессии с номером  может быть найден по формуле
может быть найден по формуле

Необходимо найти  , имеем:
, имеем:

Ответ: 39.
Задание 11 № 314628
Записаны первые три члена арифметической прогрессии: 20; 17; 14. Какое число стоит в этой арифметической прогрессии на 91-м месте?
Решение.
Определим разность арифметической прогрессии:

Член арифметической прогрессии с номером  может быть найден по формуле
может быть найден по формуле

Необходимо найти  , имеем:
, имеем:

Ответ: −250.
Задание 11 № 314653
Дана арифметическая прогрессия (аn): −6; −2; 2; …. Найдите a 16.
Решение.
Определим разность арифметической прогрессии:

Член арифметической прогрессии с номером  может быть найден по формуле
может быть найден по формуле

Необходимо найти  , имеем:
, имеем:

Ответ: 54.
Задание 11 № 316343
Выписаны первые несколько членов арифметической прогрессии: −87; −76; −65; … Найдите первый положительный член этой прогрессии.
Решение.
Определим разность арифметической прогрессии:

Член арифметической прогрессии с номером  может быть найден по формуле
может быть найден по формуле
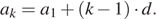
Нам же нужно найти первый положительный член этой прогрессии, т. е. нужно, чтобы выполнялось условие  Решим неравенство
Решим неравенство  :
:

Значит 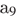 — первый положительный член этой прогрессии.
— первый положительный член этой прогрессии.

Ответ: 1.
Задание 11 № 321384
В первом ряду кинозала 24 места, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в восьмом ряду?
Решение.
Число мест в ряду представляет собой арифметическую прогрессию с первым членом  и разностью
и разностью  Член арифметической прогрессии с номером
Член арифметической прогрессии с номером 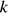 может быть найден по формуле
может быть найден по формуле

Необходимо найти  , имеем:
, имеем:

Ответ: 38.
Задание 11 № 321394
 Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 8 квадратов больше, чем в предыдущей. Сколько квадратов в 16-й строке?
Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 8 квадратов больше, чем в предыдущей. Сколько квадратов в 16-й строке?
Решение.
Число квадратов в строке представляет собой арифметическую прогрессию с первым членом  и разностью
и разностью  Член арифметической прогрессии с номером
Член арифметической прогрессии с номером 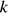 может быть найден по формуле
может быть найден по формуле

Необходимо найти  , имеем:
, имеем:

Ответ: 122.
Задание 11 № 321663
Выписано несколько последовательных членов арифметической прогрессии: …; −9; x; −13; −15; … Найдите член прогрессии, обозначенный буквой x.
Решение.
Найдем разность арифметической прогрессии:  Поэтому
Поэтому 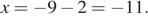
Ответ: −11.
Задание 11 № 339063
Дана арифметическая прогрессия (an), разность которой равна 2,5, a 1 = 8,7. Найдите a 9.
Решение.
Член арифметической прогрессии с номером  можно найти по формуле
можно найти по формуле  Требуется найти
Требуется найти 
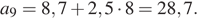
Ответ: 28,7.
Задание 11 № 340584
Даны пятнадцать чисел, первое из которых равно 6, а каждое следующее больше предыдущего на 4. Найти пятнадцатое из данных чисел.
Решение.
Последовательность, описанная в условии, образует арифметическую прогрессию с первым членом, равным шести, и разностью 4. Пятнадцатый член данной прогрессии равен: 
Ответ: 62.
Задание 11 № 341190
Дана арифметическая прогрессия (an), разность которой равна −8,5, a 1 = −6,8. Найдите a 11.
Решение.
Член арифметической прогрессии с номером  можно найти по формуле
можно найти по формуле  Требуется найти
Требуется найти 

Ответ: −91,8.
Задание 11 № 341201
Арифметическая прогрессия  задана условиями:
задана условиями:  Найдите
Найдите 
Решение.
Воспользовавшись формулой, получаем:

Ответ: −30,4.
Задание 11 № 341202
Дана арифметическая прогрессия (an), для которой a 10 = 19, a 15 = 44. Найдите разность прогрессии.
Решение.
Член арифметической прогрессии с номером n вычисляется по формуле  Зная, что a 10 = 19, b 15 = 44, получаем систему уравнений. Вычтем первое уравнение из второго и решим систему:
Зная, что a 10 = 19, b 15 = 44, получаем систему уравнений. Вычтем первое уравнение из второго и решим систему:

Ответ: 5.
Задание 11 № 341214
Арифметическая прогрессия задана условием an = −0,6 + 8,6 n. Найдите сумму первых 10 её членов.
Решение.
Сумма n первых членов арифметической прогрессии даётся формулой
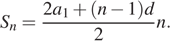
Найдем разность и первый член прогрессии:

Подставим найденные значения в формулу:

Ответ: 467.
Задание 11 № 341221
Дана арифметическая прогрессия (an), разность которой равна −2,5, a 1 = −9,1. Найдите сумму первых 15 её членов.
Решение.
Сумма n первых членов арифметической прогрессии даётся формулой

По условию, 
 откуда получаем
откуда получаем

Ответ: −399.
Задание 11 № 341492
Арифметическая прогрессия задана условием an = −11,9 + 7,8 n. Найдите a 11.
Решение.
Подставим 11 вместо индекса n:

Ответ: 73,9.
Задание 11 № 341518
Первый член арифметической прогрессии равен −11,9, а разность прогрессии равна 7,8. Найдите двенадцатый член этой прогрессии.
Решение.
Член арифметической прогрессии с номером 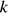 может быть найден по формуле
может быть найден по формуле

Необходимо найти  , имеем:
, имеем:

Ответ: 73,9.
Задание 11 № 341703
Дан числовой набор. Его первое число равно 6,2, а каждое следующее число на 0,6 больше предыдущего. Найдите пятое число этого набора.
Решение.
Заметим, что дана арифметическая прогрессия, первый член которой равен 6,2, а разность равна 0,6. Таким образом, пятый элемент данной прогрессии вычисляется по формуле:

Ответ: 8,6.
Задание 11 № 353273
Выписаны первые несколько членов арифметической прогрессии: −26; −20; −14; … Найдите первый положительный член этой прогрессии.
Решение.
Определим разность арифметической прогрессии:

Член арифметической прогрессии с номером 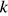 может быть найден по формуле
может быть найден по формуле

Нам же нужно найти первый положительный член этой прогрессии, т. е. нужно, чтобы выполнялось условие  Решим неравенство
Решим неравенство 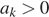 :
:

Значит  — первый положительный член этой прогрессии.
— первый положительный член этой прогрессии.
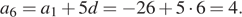
Ответ: 4.
Задание 11 № 353405
Дана арифметическая прогрессия (an), разность которой равна 1,1, a 1 = −7. Найдите сумму первых 8 её членов.
Решение.
Сумма n первых членов арифметической прогрессии даётся формулой
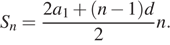
По условию, 
 откуда получаем
откуда получаем

Ответ: −25,2.
Задание 11 № 353486
Арифметическая прогрессия задана условием an = 1,9 - 0,3 n. Найдите сумму первых 15 её членов.
Решение.
Сумма n первых членов арифметической прогрессии даётся формулой

Найдем разность и первый член прогрессии:

Подставим найденные значения в формулу:

Ответ: -7,5.