Числовые последовательности

Геометрическая прогрессия

Задание 11 № 311318

В гео­мет­ри­че­ской про­грес­сии известно, что . Найти пятый член этой прогрессии.

Решение.

В силу фор­му­лы имеем:

 

 

 

Ответ: 32.

Задание 11 № 311353

Геометрическая про­грес­сия за­да­на фор­му­лой - го члена . Ука­жи­те чет­вер­тый член этой прогрессии.

Решение.

По фор­му­ле n -го члена гео­мет­ри­че­ской про­грес­сии имеем:

 

Ответ: −54.

Задание 11 № 311953

Дана гео­мет­ри­че­ская про­грес­сия (b_n), зна­ме­на­тель ко­то­рой равен 2, а 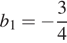. Най­ди­те сумму пер­вых шести её членов.

Решение.

Сумма n пер­вых чле­нов гео­мет­ри­че­ской про­грес­сии да­ёт­ся формулой

 

 

По условию, от­ку­да получаем

 

 

Ответ: −47,25.

Задание 11 № 314618

В гео­мет­ри­че­ской про­грес­сии сумма пер­во­го и вто­ро­го чле­нов равна 75, а сумма вто­ро­го и тре­тье­го чле­нов равна 150. Най­ди­те пер­вые три члена этой про­грес­сии.

 

В от­ве­те запишите первый, вто­рой и тре­тий члены прогрессии без пробелов.

Решение.

По усло­вию 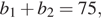За­пи­шем эти ра­вен­ства в виде си­сте­мы урав­не­ний на пер­вый член и зна­ме­на­тель про­грес­сии и решим эту систему:

 

 

Теперь найдём вто­рой и тре­тий члены прогрессии:

 

 

Ответ: 2550100.

 

Приведём другое решение.

Пусть b — первый член, а q — знаменатель прогрессии. Сумма первого и второго членов геометрической прогрессии отличается от суммы второго и третьего в q раз, поэтому q = 2. Тогда b + 2 b = 75, поэтому b = 25. Таким образом, искомые члены прогрессии равны 25, 50 и 100.

Задание 11 № 321377

Гео­мет­ри­че­ская про­грес­сия за­да­на усло­ви­ем Най­ди­те сумму пер­вых её 4 чле­нов.

Решение.

Найдём зна­ме­на­тель гео­мет­ри­че­ской прогрессии:

 

 

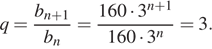
Первый член дан­ной про­грес­сии равен Сумма пер­вых чле­нов гео­мет­ри­че­ской про­грес­сии может быть най­де­на по фор­му­ле:

 

Необходимо найти , имеем:

 

Ответ: 19 200.

Задание 11 № 321553

Выписаны пер­вые не­сколь­ко чле­нов гео­мет­ри­че­ской прогрессии: 17, 68, 272,... Най­ди­те её четвёртый член.

Решение.

Найдём зна­ме­на­тель гео­мет­ри­че­ской прогрессии:

 

 

Четвёртый член про­грес­сии равен

 

Ответ: 1088.

Задание 11 № 321687

Вы­пи­са­но не­сколь­ко по­сле­до­ва­тель­ных чле­нов гео­мет­ри­че­ской про­грес­сии: …; 150; x; 6; 1,2; … Най­ди­те член про­грес­сии, обо­зна­чен­ный бук­вой x.

Решение.

Найдем зна­ме­на­тель гео­мет­ри­че­ской прогрессии: Поэтому,

 

Ответ: 30.

Задание 11 № 333009

Выписаны пер­вые не­сколь­ко чле­нов гео­мет­ри­че­ской прогрессии: −1024; −256; −64; … Най­ди­те сумму пер­вых 5 её членов.

Решение.

Найдём зна­ме­на­тель гео­мет­ри­че­ской прогрессии:

 

 

Найдём четвёртый и пятый члены про­грес­сии:

 

 

Сумма пер­вых пяти пер­вых чле­нов про­грес­сии равна

 

Ответ: −1364.

Задание 11 № 341191

Гео­мет­ри­че­ская про­грес­сия за­да­на усло­ви­ем 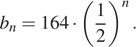Най­ди­те сумму пер­вых её 4 чле­нов.

Решение.

Найдём зна­ме­на­тель гео­мет­ри­че­ской прогрессии:

 

 

Первый член дан­ной про­грес­сии равен Сумма пер­вых чле­нов гео­мет­ри­че­ской про­грес­сии может быть най­де­на по фор­му­ле:

 

Необходимо найти имеем:

 

Ответ: 153,75.

Задание 11 № 341197

Вы­пи­са­но не­сколь­ко по­сле­до­ва­тель­ных чле­нов гео­мет­ри­че­ской про­грес­сии: …; 1,75; x; 28; −112; … Най­ди­те член про­грес­сии, обо­зна­чен­ный бук­вой x.

Решение.

Найдем зна­ме­на­тель гео­мет­ри­че­ской прогрессии: Поэтому,

 

Ответ: −7.

Задание 11 № 341198

Дана гео­мет­ри­че­ская про­грес­сия (b_n), для ко­то­рой b ₅ = −14, b ₈ = 112. Най­ди­те зна­ме­на­тель прогрессии.

Решение.

Член гео­мет­ри­че­ской про­грес­сии с но­ме­ром n вы­чис­ля­ет­ся по фор­му­ле Зная, что b ₅ = −14 и b ₈ = 112, по­лу­ча­ем си­сте­му уравнений. Решим систему, раз­де­лив вто­рое урав­не­ние на первое:

 

 

Ответ: −2.

Задание 11 № 341206

Гео­мет­ри­че­ская про­грес­сия за­да­на усло­ви­ем b ₁ = −7, b_{n + 1} = 3 b_n. Най­ди­те сумму пер­вых 5 её членов.

Решение.

Найдём зна­ме­на­тель гео­мет­ри­че­ской прогрессии:

 

 

Сумма пер­вых чле­нов гео­мет­ри­че­ской про­грес­сии может быть най­де­на по фор­му­ле:

 

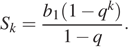
Необходимо найти имеем:

 

Ответ: −847.

Задание 11 № 341208

Дана гео­мет­ри­че­ская про­грес­сия (b_n), зна­ме­на­тель ко­то­рой равен 2, а b ₁ = 16. Най­ди­те b ₄.

Решение.

Член гео­мет­ри­че­ской про­грес­сии с но­ме­ром n можно найти по фор­му­ле b_n = b ₁ · q^{n − 1}. В нашем слу­чае n = 4:

 

 

Ответ: 128.

Задание 11 № 341217

Дана гео­мет­ри­че­ская про­грес­сия (b_n), зна­ме­на­тель ко­то­рой равен 5, а Най­ди­те сумму пер­вых 6 её членов.

Решение.

Сумма n пер­вых чле­нов гео­мет­ри­че­ской про­грес­сии да­ёт­ся формулой

 

 

По условию, 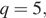от­ку­да получаем

 

 

Ответ: 1562,4.

Задание 11 № 341220

Вы­пи­са­ны пер­вые не­сколь­ко чле­нов гео­мет­ри­че­ской про­грес­сии: − 256; 128; − 64; … Най­ди­те сумму пер­вых семи её членов.

Решение.

Найдём зна­ме­на­тель гео­мет­ри­че­ской прогрессии:

 

 

Сумма пер­вых чле­нов гео­мет­ри­че­ской про­грес­сии может быть най­де­на по формуле:

 

 

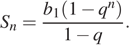
Необходимо найти , имеем:

 

 

Ответ: −172.

Задание 11 № 353212

Дана гео­мет­ри­че­ская про­грес­сия (b_n), для ко­то­рой b ₃ = , b ₆ = -196. Най­ди­те зна­ме­на­тель прогрессии.

Решение.

Член гео­мет­ри­че­ской про­грес­сии с но­ме­ром n вы­чис­ля­ет­ся по фор­му­ле Зная, что b ₃ = и b ₆ = -196, по­лу­ча­ем си­сте­му уравнений. Решим систему, раз­де­лив вто­рое урав­не­ние на первое:

 

 

Ответ: −7.

Задание 11 № 353420

Гео­мет­ри­че­ская про­грес­сия за­да­на усло­ви­ем b ₁ = −3, b_{n + 1} = 6 b_n. Най­ди­те сумму пер­вых 4 её членов.

Решение.

Найдём зна­ме­на­тель гео­мет­ри­че­ской прогрессии:

 

 

Сумма пер­вых чле­нов гео­мет­ри­че­ской про­грес­сии может быть най­де­на по фор­му­ле:

 

Необходимо найти имеем:

 

Ответ: −777.

Задание 11 № 353437

Вы­пи­са­но не­сколь­ко по­сле­до­ва­тель­ных чле­нов гео­мет­ри­че­ской про­грес­сии: …; -12; x; -3; 1,5; … Най­ди­те член про­грес­сии, обо­зна­чен­ный бук­вой x.

Решение.

Найдем зна­ме­на­тель гео­мет­ри­че­ской прогрессии: Поэтому,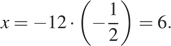

 

Ответ: 6.

 

 

Числовые последовательности

Задание 11 № 137294

Последовательность за­да­на фор­му­лой . Какое из ука­зан­ных чисел яв­ля­ет­ся чле­ном этой последовательности?

 

1) 1

2) 2

3) 3

4) 4

Решение.

Рассмотрим не­сколь­ко пер­вых чле­нов последовательности, на­чи­ная с

 

 

 

Тем самым, число 3 яв­ля­ет­ся чле­ном этой последовательности.

 

Ответ: 3.

Задание 11 № 137295

Последовательность за­да­на фор­му­лой . Какое из сле­ду­ю­щих чисел не яв­ля­ет­ся чле­ном этой последовательности?

 

1)

2)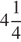

3)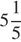

4)

Решение.

Рассмотрим не­сколь­ко пер­вых чле­нов последовательности, на­чи­ная с

 

 

 

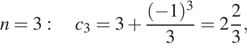
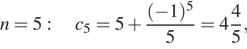
Тем самым, число не яв­ля­ет­ся чле­ном этой последовательности.

 

Ответ: 3.

Задание 11 № 137296

Какое из ука­зан­ных чисел не яв­ля­ет­ся чле­ном по­сле­до­ва­тель­но­сти

 

1)

2)

3)

4)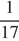

Решение.

Рассмотрим не­сколь­ко пер­вых чле­нов последовательности, на­чи­ная с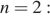

 

 

 

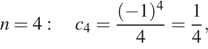
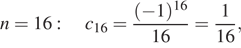
Тем самым, не яв­ля­ет­ся чле­ном этой последовательности.

 

Ответ: 4.

Задание 11 № 137297

Последовательность за­да­на фор­му­лой . Сколь­ко чле­нов в этой по­сле­до­ва­тель­но­сти боль­ше 1?

 

1) 8

2) 9

3) 10

4) 11

Решение.

Дробь, чис­ли­тель и зна­ме­на­тель ко­то­рой положительны, боль­ше единицы, если чис­ли­тель боль­ше знаменателя. Поэтому, имеем: Таким образом, пра­виль­ный ответ ука­зан под но­ме­ром 2.

 

Ответ: 2.

Задание 11 № 137298

Последовательности за­да­ны не­сколь­ки­ми пер­вы­ми членами. Одна из них — ариф­ме­ти­че­ская прогрессия. Ука­жи­те ее.

 

1)

2)

3)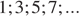

4) ; ; ; ;...

Решение.

Арифметической про­грес­си­ей на­зы­ва­ет­ся такая по­сле­до­ва­тель­ность в ко­то­рой раз­ность между по­сле­ду­ю­щим и преды­ду­щим чле­на­ми про­грес­сии оста­ет­ся неизменной. По­это­му ариф­ме­ти­че­ская про­грес­сия яв­ля­ет­ся последовательность: 1; 3; 5;... Таким образом, пра­виль­ный ответ ука­зан под но­ме­ром 3.

 

Ответ: 3.

Задание 11 № 137299

Одна из дан­ных по­сле­до­ва­тель­но­стей яв­ля­ет­ся гео­мет­ри­че­ской прогрессией. Ука­жи­те эту последовательность.

 

1)

2)

3)

4) ; ; ; ;...

Решение.

Геометрической про­грес­си­ей на­зы­ва­ют чис­ло­вую последовательность, пер­вый член ко­то­рой от­ли­чен от нуля, а каж­дый последующий, равен предшествующему, умно­жен­но­му на одно и тоже от­лич­ное от нуля число. По­это­му гео­мет­ри­че­ской про­грес­си­ей яв­ля­ет­ся последовательность: 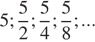Таким образом, пра­виль­ный ответ ука­зан под но­ме­ром 2.

 

Ответ: 2.

Задание 11 № 137300

Какая из сле­ду­ю­щих по­сле­до­ва­тель­но­стей яв­ля­ет­ся ариф­ме­ти­че­ской прогрессией?

 

1) По­сле­до­ва­тель­ность на­ту­раль­ных сте­пе­ней числа 2.

2) По­сле­до­ва­тель­ность на­ту­раль­ных чисел, крат­ных 5.

3) По­сле­до­ва­тель­ность кубов на­ту­раль­ных чисел.

4) По­сле­до­ва­тель­ность всех пра­виль­ных дробей, чис­ли­тель ко­то­рых на 1 мень­ше знаменателя.

Решение.

Ариф­ме­ти­че­ской про­грес­си­ей на­зы­ва­ет­ся такая по­сле­до­ва­тель­ность в ко­то­рой раз­ность между по­сле­ду­ю­щим и преды­ду­щим чле­на­ми про­грес­сии оста­ет­ся не­из­мен­ной. По­это­му ариф­ме­ти­че­ская про­грес­сия яв­ля­ет­ся по­сле­до­ва­тель­ность: 5; 10; 15;... Таким об­ра­зом, пра­виль­ный ответ ука­зан под но­ме­ром 2.

 

Ответ: 2.

Задание 11 № 137306

Последовательность за­да­на усло­ви­я­ми , . Най­ди­те .

Решение.

Будем вы­чис­лять последовательно: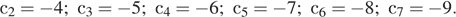

Данная по­сле­до­ва­тель­ность об­ра­зу­ет ариф­ме­ти­че­скую прогрессию. Най­дем раз­ность ариф­ме­ти­че­ской прогрессии:

тогда

 

Примечание.

Зная раз­ность и пер­вый член ариф­ме­ти­че­ской прогрессии, можно найти посредственно:

 

 

 

Ответ: −9.

Задание 11 № 137307

Последовательность за­да­на усло­ви­я­ми , 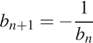. Най­ди­те .

Решение.

Найдём не­сколь­ко пер­вых чле­нов последовательности:

 

 

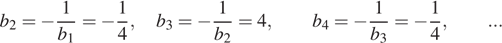
Отсюда ясно, что все члены по­сле­до­ва­тель­но­сти с нечётными но­ме­ра­ми равны 4.

 

Ответ: 4.

 

Примечание.

Из ре­кур­рент­ной формулы, за­да­ю­щей n -й член последовательности, можно не­по­сред­ствен­но получить, что

 

 

Отсюда ясно, что все члены по­сле­до­ва­тель­но­сти с нечётными но­ме­ра­ми равны пер­во­му члену последовательности, а все члены по­сле­до­ва­тель­но­сти с чётными равны вто­ро­му члену последовательности.

Задание 11 № 341203

Последовательность за­да­на фор­му­лой 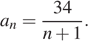Сколь­ко чле­нов в этой по­сле­до­ва­тель­но­сти боль­ше 6?

Решение.

Необходимо ре­шить неравенство:

 

 

Поскольку n — целые числа, не­ра­вен­ство выполняется при n рав­ном 1, 2, 3 и 4. Таким образом, че­ты­ре члена дан­ной последовательности боль­ше 6.

 

Ответ: 4.

Задание 11 № 341669

Сколько на­ту­раль­ных чисел n удо­вле­тво­ря­ет не­ра­вен­ству ?

Решение.

Дробь, чис­ли­тель и зна­ме­на­тель ко­то­рой положительны, боль­ше двух, если чис­ли­тель боль­ше зна­ме­на­те­ля более чем в два раза. Поэтому, имеем: Таким образом, во­сем­на­дцать на­ту­раль­ных чисел удо­вле­тво­ря­ют дан­но­му неравенству.

 

Ответ: 18.

Задание 11 № 351753

Последовательность за­да­на фор­му­лой . Сколь­ко чле­нов в этой по­сле­до­ва­тель­но­сти боль­ше 3?

Решение.

Таким образом, пра­виль­ный ответ 4.

 

Ответ: 4.