Есть разные интерполяционные полиномы — функции, определяющие как будут изменяться приближенные значения между узловыми точками:
Канонический полином
Полином Лагранжа
Полином Ньютона
Пример:
Для начала необходимо создать функцию, по которой Matlab будет считать. Создайте файл с именем «lagrange» и запишем в него:
function yy=lagrange(x,y,xx)
% вычисление интерполяционного полинома в форме Лагранжа
% x - массив координат узлов
% y - массив значений интерполируемой функции
% xx - массив значений аргумента, для которых надо вычислить значения полинома
% yy - массив значений полинома в точках xx
% узнаем число узлов интерполяции (N=n+1)
N=length(x);
% создаем нулевой массив значений интерполяционного полинома
yy=zeros(size(xx));
% в цикле считаем сумму по узлам
for k=1:N
% вычисляем произведения, т.е. функции Psi_k
t=ones(size(xx));
for j=[1:k-1, k+1:N]
t=t.*(xx-x(j))/(x(k)-x(j));
end
% накапливаем сумму
yy = yy + y(k)*t;
end
Теперь создайте ещё один файл и запишем в него само решение поставленной задачи:
% задание узлов интерполяции
x=1:2:9;
y=sin(x);
% задание точек, в которых требуется найти значения интерполяционного полинома
xx=linspace(1,9,1000);
% нахождение значений интерполяционного полинома
yy=lagrange(x,y,xx);
% построение графиков
figure('Color','w')
% вывод графика sin(x)
fplot(@sin,[1 9])
hold on
% вывод графика полинома
plot(xx,yy,'r')
% вывод узлов интерполяции
plot(x,y,'bo')
% размещение легенды
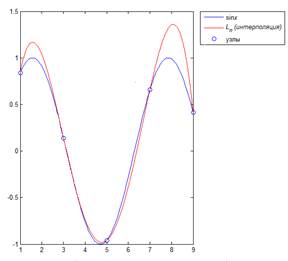
legend('sin\itx','{\itL_n (интерполяция)}','узлы',-1)
Интерполяция сплайнами
Сплайн — это группа кубических многочленов, которые также называют кубическими сплайнами.
Вычисление сплайн интерполяции в Matlab осуществляется с помощью команды spline(x, y, xx), где х и у — массивы табличных данных, а хх — промежуточные значения по оси абцисс (Х).
Вот небольшой пример:
Построить интерполяцию сплайнами функции Рунге.
% Введём функцию Рунге
f = inline('1./(1+25*x.^2)');
% Вычислим таблицу значений
x = linspace(-1, 1, 10);
y = f(x);
% Вычислим сплайн-интерполяцию
xx = linspace(-1, 1, 100);
yy = spline(x, y, xx);
% Начертим графики
axes('NextPlot','Add');
plot(x, y,'LineWidth', 2);
% Красным на графике - аппроксимация, жирным - исходная функция
plot(xx, yy,'Color','r');
Вывод:

interp1
Большинство задач в Matlab реализуются с помощью этой команды. yi = interp1 (x,y,xi, metod), где х – массив абсцисс экспериментальных точек, у – массив ординат экспериментальных точек, xi — точки, в которых необходимо вычислить значения с помощью сплайна, metod – определяет метод построения сплайна. Этот параметр может принимать следующие значения:
‘nearest’ – интерполяция по соседним точкам – этот метод построения кусочной функции, при котором значение в любой точке равно значению в ближайшей узловой точке – интерполяция полиномами 0-ой степени;
‘linear’ – линейная сплайн-интерполяция — интерполяция полиномами 1-ой степени (применяется по умолчанию, если способ интерполирования не задан);
‘cubic’ – интерполяция кубическим полиномом;
‘spline’ – интерполяция кубическим сплайном;
‘pchip’ — интерполяция кубическим эрмитовым сплайном.
Интерполяция на неравномерной сетке
Для интерполяции на неравномерной сетке используется функция griddata:
ZI = griddata(x.y.z.XI.YI) – преобразует поверхность вида z = f(x. у), которая определяется векторами (x.y.z) с (обычно) неравномерно распределенными элементами. Функция griddata аппроксимирует эту поверхность в точках, определенных векторами (XI.YI) в виде значений ZI. Поверхность всегда проходит через заданные точки. XI и YI обычно формируют однородную сетку (созданную с помощью функции meshgrid).
XI может быть вектором-строкой, в этом случае он определяет матрицу с постоянными столбцами. Точно так же YI может быть вектором-столбцом, тогда он определяет матрицу с постоянными строками.
[XI.YI.ZI] = griddata(x,y,z,xi,yi) – возвращает аппроксимирующую матрицу ZI, как описано выше, а также возвращает матрицы XI и YI, сформированные из вектора-столбца xi и вектора-строки yi. Последние аналогичны матрицам, возвращаемым функцией meshgrid;
[…] = griddata (….method) – использует определенный метод интерполяции:
'nearest' – ступенчатая интерполяция;
'linear' – линейная интерполяция (принята по умолчанию);
'cubic' – кубическая интерполяция;
' v4 ' – метод, используемый в МATLAB 4.
Метод определяет тип аппроксимирующей поверхности. Метод 'cubic' формирует гладкие поверхности, в то время как 'linear' и 'nearest' имеют разрывы первых и нулевых производных соответственно. Все методы, за исключением v4, основаны на триангуляции Делоне. Метод ' v4 ' включен для обеспечения совместимости с версией 4 системы MATLAB. Пример:
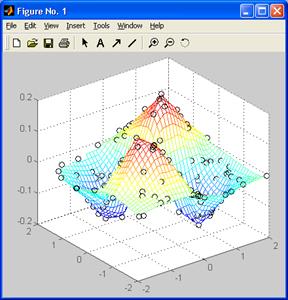
>> x=rand(120.1)*4-2;y=rand(120.1)*4-2;
z=x,*y,*exp(-x.^2-y.^2);
>> t=-2:0.1:2;[X,Y]=meshgrid(t,t);
Z=griddata(x.y.z.X.Y);
>> mesh(X.Y.Z),hold on;plot3(x.y,z, 'ok')
Функции griddataS и griddatan работают аналогично griddata, но для для трехмерного и n-мерного случая – с использованием алгоритма qhul 1. Используются, в частности, при трехмерной и n-мерной триангуляции.