Куб
Кубом называется прямоугольный параллелепипед с равными ребрами.
| Объем тела | Площадь боковой поверхности | Площадь основания | Площадь полной поверхности |
| V = a3 | S = 4 a2 | S = a2 | S = 6 a2 |
1. Диагонали куба пересекаются в точке, являющейся центром вписанной и описанной сфер.
2. Радиус описанной около куба сферы равен 
.
3. Радиус вписанной в куб сферы равен 
.
Задачи
1. Диагональ куба равна 
. Найдите его объем.
Ответ: 8.
2. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 30. Найдите ребро куба.
Ответ: 2.
3.В куб с ребром 6 вписан шар. Найдите объем шара, деленный на 
.
Ответ: 36.
4. Диагональ куба равна 
. Найдите его объем.
Ответ: 27.
5. Диагональ грани куба равна 
. Найдите его объем.
Ответ: 8.
6.Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.
Ответ: 2.
7. Во сколько раз увеличится объем куба, если его ребра увеличить в три раза?
Ответ: 27.
8. Диагональ куба равна 1. Найдите площадь его поверхности.
Ответ: 2.
9. Площадь поверхности куба равна 8. Найдите его диагональ.
Ответ: 2.
10. Диагональ грани куба равна 3. Найдите площадь его поверхности.
Ответ: 27.
11. Площадь поверхности куба равна 48. Найдите диагональ грани куба.
Ответ: 4.
12. Диагональ куба равна 
. Найдите его объем.
Ответ: 27.
13. Площадь поверхности куба равна 24. Найдите его объем.
Ответ: 8.
14. Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в три раза?
Ответ: 9.
15. Объем куба равен 27. Найдите площадь его поверхности.
Ответ: 54.
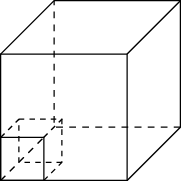
16. Объем куба равен 12. Найдите объем треугольной пирамиды, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины.
Ответ: 1,5.
Прямоугольный параллелепипед
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
| Объем тела | Площадь боковой поверхности | Площадь основания | Площадь полной поверхности |
| V=SоснH | S=2(a+b)c | S = ab | S= Sбок+2Sосн |
| V =abc | |||
| V=abH | S=2ab+2ac+2bc |
Противоположные грани прямоугольного параллелепипеда – равные прямоугольники.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерении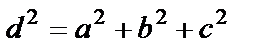 
.
Задачи
1. Диагональ прямоугольного параллелепипеда равна 
и образует углы 30о, 45о и 60о с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.
Ответ: 4,5.
2. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 2. Найдите объем параллелепипеда.
Ответ: 32.
3. Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого равны 90о.
Ответ: 7.
4. Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
Ответ: 8.
5. Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани.
Ответ: 5.
6. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
Ответ: 32.
7. Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3, 4, 5. Найдите площадь его поверхности.
Ответ: 94.
8. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 52. Найдите третье ребро, выходящее из той же вершины.
Ответ: 2.
9. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда.
Ответ: 64.
10. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.
Ответ: 3.
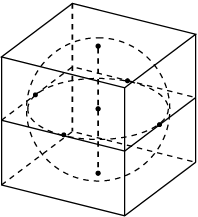
11. Прямоугольный параллелепипед описан около сферы радиуса 2. Найдите площадь его поверхности.
Ответ: 96.
12. Прямоугольный параллелепипед описан около сферы радиуса 2. Найдите его объем.
Ответ: 64.
13. Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы.
Ответ: 3.
14. Площадь поверхности прямоугольного параллелепипеда, описанного около сферы, равна 96. Найдите радиус сферы.
Ответ: 2.
15. Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
Ответ: 48.
16. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
Ответ: 4.
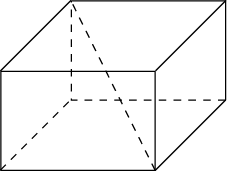
17. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ.
Ответ: 7.
Призма
| призма |
| прямая призма |
Многогранник, две грани которого равные многоугольники, лежащие в параллельных плоскостях, а остальные грани параллелограммы, называется призмой.
Равные многоугольники, лежащие в параллельных плоскостях, называются основаниями призмы. Остальные грани называются боковыми гранями. Они образуют боковую поверхность призмы. Различают ребра при основании и боковые ребра призмы (L).
Призма называется прямой, если боковые ребра перпендикулярны основаниям призмы.
Перпендикуляр, опущенный из любой токи верхнего основания на нижнее основание, называется высотой призмы (Н).
Название призмы зависит от многоугольника, лежащего в основании призмы.
Полная поверхность призмы равна сумме площадей двух оснований и площади боковой поверхности.
Боковая поверхность призмы равна произведению периметра основания на высоту призмы. 
(Или, произведению периметра перпендикулярного сечения на боковое ребро призмы 
).
Объем призмы равен произведению площади основания на высоту призмы.
(Или, произведению площади перпендикулярного сечения на боковое ребро призмы 
).
Призма, в основании которой лежит параллелограмм, называется параллелепипедом.
Все противоположные грани параллелепипеда равны и параллельны. Диагонали параллелепипеда пересекаются в одной точке и делятся в ней пополам. Точка пересечения диагоналей является центром симметрии параллелепипеда.
Параллелепипед, все грани которого прямоугольники, называется прямоугольным параллелепипедом.
Прямоугольный параллелепипед с равными ребрами называется кубом.
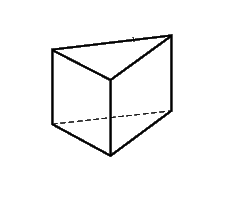
Прямая призма (треугольная правильная)
Призма, у которой боковые ребра перпендикулярны основаниям, а основания – правильные треугольники.
| Объем тела | Площадь боковой поверхности | Площадь основания | Площадь полной поверхности |
| V=SоснH | S=3aH |  
| S= Sбок+2Sосн |
| 
|
1. Боковые грани – равные прямоугольники
2. Сторона основания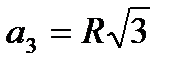 
Задачи
1. Найдите объем правильной треугольной призмы, все ребра которой равны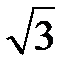 
.
Ответ: 2,25.
2. Объем правильной треугольной призмы равен 6. Каким будет объем призмы, если стороны ее основания увеличить в три раза, а высоту уменьшить в два раза?
Ответ: 27.
3. Площадь поверхности правильной треугольной призмы равна 6. Какой будет площадь поверхности призмы, если все ее ребра увеличить в три раза?
Ответ: 54.
4. В сосуд, имеющий форму правильной треугольной призмы, налили 2300 см3 воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см.
Найдите объем детали. Ответ выразите в см3.
Ответ:184
5.В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.
Ответ:5