Ответ:
Тип проводимости можно измерить методом термозонда.
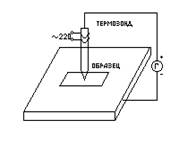
Образец помещается на массивную МЕ пластинку, служащую холодным контактом. Нагретым с помощью электронагревателя зондом касаются верхней поверхности образца. Если образец n-типа, то электроны в образце диффундируют от нагреваемой термозондом верхней грани к холодной нижней грани, заряжая ее отрицательно. Верхняя грань образца будет заряжаться положительно за счет остающихся нескомпенсированными ионов донорной примеси. Если образец p-типа, то к холодной грани образца диффундируют положительные дырки, оставляя на горячей грани отрицательный заряд нескомпенсированных ионов акцепторов. Таким образом, холодная грань образца заряжается знаком основных носителей заряда, который можно установить по направлению стрелки гальванометра в цепи термозонда. Еще можно определить тип проводимости из эффекта Холла по знаку коэффициента Холла, но метод термозонда более достоверный (точный) и поэтому он предпочтительнее.
1.9. Какие методы измерения электропроводности полупроводников вы знаете?
Ответ:
а) Зондовые методы: В этих методах осуществляется прямое измерение сопротивления определенной области образца по величине падения напряжения на ней при протекании определенного электрического тока. Они основаны на законе Ома. Существуют: однозондовый, двухзондовый, четырехзондовый методы.
б) Бесконтактные высокочастотные методы: Основаны на зависимости свойств скин-слоя, характеризующего глубину проникновения высокочастотного электрического поля в образец от величины его электропроводности. Бывают: емкостные(образец становится частью измерительного конденсатора) и индуктивные(образец помещается в катушку индуктивности) методики. Можно измерять сопротивление в поликристаллических образцах, так как влияние существенно более высокоомных межкристаллитных прослоек слабо сказывается в высокочастотных измерениях.
с) Оптические методы: Основаны на анализе данных по поглощению или отражению света в среде кристалла. Методы эти неразрушающие, и чувствительные даже в области очень низкоомных сильнолегированных образцов.
1.10. Каковы условия выполнения закона Ома? Дайте численные промеры выполнения этих условий (в рамках элементарной теории электропроводности).
Ответ:
Условия выполнения: 1) закон Ома имеет место только в слабых электрических полях. 2) vДР << vТ.
Численный пример: vДР = 10-7 м/с vТ = 105 м/с è 10-7 << 105.
1.11. Каковы причины суперлинейного роста плотности электрического тока в полупроводниках? Как оценить порядок величины (Ēкр) напряженности электрического поля в этом случае?
Ответ:
Суперлинейный рост плотности электрического тока в п/п наблюдается за счет влияния электрического поля на концентрацию носителей заряда (концентрация растет в области сильных электрических полей за счет эффектов ударной ионизации или туннельного механизма генерации носителей заряда). Порядок величины определяется из соотношения: |Екр| = vДР/m, т.е. зная порядки дрейфовой скорости и подвижности можно найти порядок Екр. Екр=105 В/м
1.12. Как оценить длину свободного пробега электрона (дырки) в рамках теории Друде-Лоренца? В чем «слабые» места этой теории?
Ответ:
Длину свободного пробега в теории Друде-Лоренца можно оценить исходя из следующей формулы: l = tСВ(vДР + vТЕПЛ) = (10-12… 10-14)*107 » 10-5…10-7 см.
Слабые места: 1). Теория не учитывает распределение по временам свободного пробега, т.е. tРЕЛ =tС/2, в то время как должно быть tРЕЛ =tс. 2) Длина свободного пробега аномально большая, порядка нескольких сотен постоянных решетки.
1.13. Каково соотношение вклада собственной и примесной электропроводности полупроводника в различных температурных интервалах? Когда можно полагать электропроводность монополярной, а когда нет?
Ответ:
а) Температурная зависимость электропроводности делится на три температурных интервала: 1) Область примесной ионизации, происходит рассеяние на ионах примеси, примесная электропроводность. 2) Область истощения примеси, плато концентрации. 3) Область собственной ионизации, рассеяние на тепловых колебаниях решетки, собственная проводимость.

б) В собственных п/п: n>>p или p>>n, в примесных п/п: ND >> NA или NA >> ND, - связь монополярна. Связь можно считать монополярной, когда одним типом носителей заряда можно пренебречь по сравнению с другим, в связи с его ничтожностью.
1.14. Какие паразитные условия сопутствуют зондовым методам измерения электропроводности полупроводников, и как устраняется их влияние на результаты измерения?
Ответ:
А). На контакте зонд-полупроводник возникает контактная разность потенциалов (потенциальный барьер для основный носителей заряда). Избавиться от нее можно с помощью компенсационного метода измерения падения напряжения или обычного цифрового вольтметра с большим входным сопротивлением. Нужно добиться того, чтобы ток в контактах зонда был равен 0, а сопротивление было очень большим. Сопротивление контактов зонда должно быть на несколько (3-4) порядков выше сопротивления образца.
Б). Паразитные термо-эдс: причина возникновения – градиент температуры, возникающий в образце при неравномерном нагревании. Устраняются с помощью двух измерений падения напряжения U+ и U- при двух разных направлениях тока. Неодходимо делать токовые контакты омическими, чтобы устранить эффект Пельтье(нагревание или охлаждение контакта в зависимости от направления тока). Омичность токовых контактов избавит также от влияния явлений инжекции, эксклюзии, экстракции и аккумуляции в приконтактных областях образца.
1.15. Какие примеси используются для управления величиной и типом электропроводности полупроводников IV группы таблицы Менделеева? А для полупроводников АIIIВV или АIIВVI? Каков общий принцип выбора легирующей примеси для n- или p-типа проводимости? Как составляется название марки полупроводникового материала?
Ответ:
а) Для элементов IV подгруппы самыми лучшими будут элементы III и V подгрупп. Акцепторная примесь - III группа, донорная – V. Для AIIIBV – II и VI группы, а AIIBVI – I и VII. Общий принцип выбора: рядом стоящий в таблице с легируемым элементом слева – акцептор, а справа – донор. б) Марки п/п: КЭФ-40, КДБ-40. 40 à r = 40 Ом*см.
1.16. Как в рамках теории Друде-Лоренца доказать равенство времени релаксации проводимости и времени свободного пробега электронов?
Ответ:
Учитывая статистической закон и функцию распределения по временам свободного пробега: 0 < tСВ < ¥, <tСВ> = t0 – среднее время.
Вероятность: w(t)=1/t0*exp(-t/t0), где t0 = t.
Имеем:  ,
,
т.к. 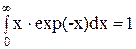 . С учетом распределения по временам свободного пробега:
. С учетом распределения по временам свободного пробега: 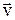 ДР = <
ДР = < 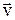 (t)> =
(t)> =  , откуда tРЕЛ = t0 = <tСВ>.
, откуда tРЕЛ = t0 = <tСВ>.
В рамках теории Друде-Лоренца предполагается, что средняя скорость направленного движения электронов сразу после соударения равна 0, т.е. электрон передает решетке, накопленную в электрическом поле во время свободного пробега энергию, в одном столкновении. Релаксация по энергии происходит за время свободного пробега: tРЕЛ =tСВ.
1.17. Каково распределение по временам и длинам свободного пробега. Как рассчитать среднюю дрейфовую скорость или среднее время свободного пробега (с помощью этого распределения)?
Ответ:
Функции распределения: По временам см. 1.17. По длинам w(x) =  , где l - среднее значение длины свободного пробега.
, где l - среднее значение длины свободного пробега.
Средняя дрейфовая скорость см. 1.17. Среднее время свободного пробега:
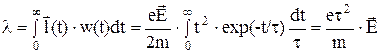 , где l – среднее смещение.
, где l – среднее смещение.
1.18. Что такое «энергия активации проводимости» и как ее экспериментально найти? Что она выражает в случае собственной и примесной проводимости, и каков ее порядок в этих случаях?
Ответ:
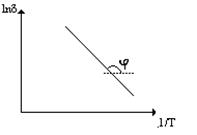
Энергия активации проводимости – важная характеристика полупроводника, определяющая электропроводность и многие другие свойства п/п. Чем меньше энергия активации проводимости, тем быстрее растет электропроводность п/п с температурой. Энергия активации может быть экспериментально определена из наблюдения температурной зависимости проводимости: lnsП = lnsП0 - dЕакт/к0Т. При построении графика в осях lns = f(1/T), экспериментальные точки ложатся на прямую, тангенс угла которой к оси абсцисс, умноженный на –к0, даст энергию активации проводимости. В случае собственной проводимости, она выражает ширину запрещенной зоны (Еg0), в случае примесной – энергию ионизации примеси (DЕd).
1.19. Что «такое подвижность носителей заряда», и как она вычисляется в рамках теории Друде-Лоренца (приведите примеры порядков величины)?
Ответ:
«Подвижность носителей заряда» - характеристический параметр материала, численно равный дрейфовой скорости в электрическом поле единичной напряженности: m = et/m – 103-105 см2/(В*с). Формулы для вычисления: m = et/m; m = vДР/Е.
Примеры величины: Si - mn (300) = 1350, mP (300) = 480; Ge: mn (300) = 3900, mP (300) = 1900 см2/(В*с)
1.20. Как в соответствии с теорией Друде-Лоренца происходит релаксация скорости направленного движения v(t) при включении и выключении электрического поля Е-const?
Ответ:
А). Включенное поле. Запишем уравнение движения электрона: mdv/dt = enE – mv/t, где mv/t - описывает силу сопротивления. Общее решение уравнения c учетом начальных условий: v(t) = entE(1 – exp(-t/t))/m. Частное решение: v1 = entE/m. Из решения уравнения видно, что после включения электрического поля за время t>>t скорость приобретает стационарное значение etE/m, имеющее смысл средней дрейфовой скорости электрона в электрическом поле: vДР = v(t)|t>>t = entE/m.
Б) Выключенное поле. В случае установления равновесия после выключения электрического поля Е в момент t=t0, уравнение движения с учетом начальных условий выглядит так: E(t) = à1) E при t < t0, 2) 0 при ³ t0. Преобраз. к виду mdv/dt = -mv/t с нач. услов. v(t0) = entE/m. Решение уравнения: v(t) = entE*exp((-t-t0)/t)/m при t=t0. Это означает, что за время t = t после выключение электрического поля, средняя скорость электрона падает в е-раз за счет сил сопротивления.
1.21. В чем отличия «дрейфовой» и «тепловой» скоростей электронов в рамках теории Друде-Лоренца (как оценить численное значение этих величин)?
Ответ:
Дрейфовая скорость – скорость направленного движения носителей заряда: vд=mE=10-7м/с.
Тепловая скорость – скорость хаотического движения носителей заряда: vT=  . =1,18 * 105 м/с.
. =1,18 * 105 м/с.
Основные отличия: 1) скорость vДР зависит от величины приложенного электрического поля, а vT зависит от температуры. 2) vДР зависит от взаимодействия электронов с кристаллической решеткой. 3) У vТ вследствие хаотичности среднее смещение и средняя v(скорость) за большой промежуток времени = 0.
1.22. Изменением каких характеристик электронного газа объясняется различное поведение температурной зависимости электропроводности в полупроводниках и металлах?
Ответ:
2-й модуль.
2.1. Напишите и дайте общую характеристику оператора Гамильтона Ĥ для идеального кристалла.
Ответ:
Оператор гамильтона включает в себя:
-оператор кинетической энергии электронов  , где
, где  - постоянная планка h., делённая на 2p, m0-масса электрона; (
- постоянная планка h., делённая на 2p, m0-масса электрона; (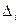 =
= 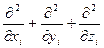 )-оператор Лапласа для i- ого электрона
)-оператор Лапласа для i- ого электрона
-оператор кинетической энергии ядер 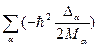 , где Ma-масса ядра; (
, где Ma-масса ядра; (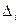 =
= 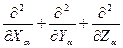 )
)
-потенциальную энергию попарного взаимодействия электронов 1/2 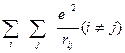
-потенциальную энергию попарного взаимодействия ядер V0(R1,R2…...., RN)
потенциальную энергию попарного взаимодействия электронов с ядрами U(r1, r2, …,R1,R2…..RN))
2.2. Какие упрощающие предположения нужно сделать, чтобы выделить из уравнения Шредингера для идеального кристалла уравнение для одного электрона в идеальном кристалле (в чем сущность этих приближений и каков результат)?
Ответ:
Предположения: 1) Ур-ние для системы частиц нужно представить системой уравнений, каждое из которых описывает движение одной частицы. 2). Невзаимодействие частиц друг с другом. В этом случае ур-ние Шредингера принимает вид: Ĥi Yi = Ei Yi.
Метод адиабатического приближения (приближение Борна-Оппенгеймера): Сущность его заключается в учете разного характера движения электронов и ядер: электроны как более легкие частицы движутся гораздо быстрее ядер, вследствие чего можно считать, что ядра остаются в покое относительно мгновенного положения электронов. Физический смысл и результат этого приближения состоит в том, что движение электронов и ядер можно считать независимыми, т.е.: Yкр = Yяд*Yэл, Eкр=Еяд*Еэл
Одноэлектронное приближение: Вводится для дальнейшего упрощения адиабатического приближения. Сущность заключается в представлении гамильтониана уравнения зависимым только от одной частицы. Выводы: 1) Ĥэл = 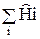 , 2) Еэл =
, 2) Еэл = 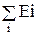 , а также приближение Хартри:
, а также приближение Хартри: 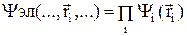
2.3. Какое свойство одноэлектронного уравнения Шредингера для электрона в идеальном кристалле использовал Блох (и как?) для определения свойств и вида волновой функции и закона дисперсии электрона?
Ответ:
Блох использовал свойство периодичности: U(r) = U(r+n). Трансляционное свойство принимает вид: Yk(r+n) = Yk(r)exp(ik,r), откуда Yk(r+n) = jК(r), Yk(r) = jК(r)exp(ik,r), где Yk(r) является решением уравнения Шредингера для электрона в кристалле, которое представляет собой плоскую волну промодулированную по амплитуде, с периодом равным постоянной решетке кристалла (т.е. волна Блоха).
Yk(r) = Аexp(ik,r) – волна де Бройля, Е = Е(к) = hk/2m – закон дисперсии.
2.4. Что такое «зона Бриллюэна», для чего она вводится и как выглядит для важнейших классов полупроводников АIV, АIIIВV, АIIВVI? Каковы главные особые точки?
Ответ:
Объем к-пространства, который соответствует периоду изменения волновой функции Yk(r) и Е(к) в к-пространстве называют зоной Бриллюэна. т.Г – центр зоны Бриллюэна.
т.X – оси типа 100 – 6 осей, центр квадратной грани; т.L –оси типа 111 – 8 осей, центр шестиугольной грани. Выглядит, как четырнадцатигранник.
2.5. Как изображаются зонная структура энергии электронов в кристалле в пределах его зоны Бриллюэна? Какие характеристики, на каких чертежах изображаются?
Ответ:
Объем к-пространства, который соответствует периоду изменения волновой функции Yk(r) и Е(к) в к-пространстве называют зоной Бриллюэна. Е(к) – зонный спектр в зоне Бриллюэна.
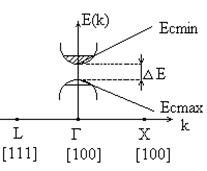
Рис. Зонная структура GaAs.
т.Г – центр зоны Бриллюэна.
т.X – оси типа 100 – 6 осей типа X., т.L –оси типа 111 – 8 осей.
2.6. Каков алгоритм описания зонной энергии электрона в кристалле? Какие важнейшие параметры зонной структуры приводятся в справочных таблицах (дайте примеры)?
Ответ:
Описание по зонно:
1 Валентная зона: из скольких подзон состоит, в какой точке EV max; max Emax эффективной массы, рас. Сечение плоскостью.
2 Зона проводимости: где находится EC min, по какому направлению, на каком расстоянии, EC=…
 Определяется число эквивалентных экстремумов (количество долин зоны проводимости), каков переход EV max EC min. Определение поверхности E(k)=const в
Определяется число эквивалентных экстремумов (количество долин зоны проводимости), каков переход EV max EC min. Определение поверхности E(k)=const в
 mt
mt
окрестности EC min. Описать тензор mn*= mf
k=me/mf;
 Число полных долин EC min (полных постоянных энергий в зоне Бриллюэна).
Число полных долин EC min (полных постоянных энергий в зоне Бриллюэна).
3 Запрещенная зона - прямая (непрямая): DET= EC min – EC max T=300 =…, DЕопт = …
4 Определить тип решетки и описать расположение электронов: spdf…(число вырожд.)
Табличные значения: см. таблицу.
2.7. К каким свойствам (волновым или корпускулярным) относятся характеристики: импульс и квазиимпульс, масса, трансляционные свойства волновой функции в r- и k-пространстве, эффективная масса, закон дисперсии, скорость?
Ответ:
Импульс – частица (корпускулярные свойства).
Квазиимпульс – волна (волновые свойства).
Масса – частица.
Трансляционные свойства – волна.
Эффективная масса – волна.
Закон дисперсии – волна.
Скорость – частица.
2.8. Как вводится и что характеризует величина эффективной массы электрона (или дырки) в кристалле? Приведите примеры для конкретных полупроводников.
Ответ:
Масса электрона вводится как масса электрона в кристалле, выводится из закона дисперсии Е(к): m* = h2/(d2E/dk2). Величина эффективной массы характеризует влияние идеальной кристаллической решетки на движение электрона в кристалле под действием внешней силы. Примеры: см. таблицу.
2.9. В чем сущность «метода эффективной массы» и как он применяется для решения задачи об электроне в неидеальном кристалле?
Ответ:
Сущность метода заключается в том, что вместо решения уравнения Шредингера с некоторым возбуждением W, локализованным в небольшой области VR, можно решать ур-ние Шредингера для свободного электрона, если вместо массы свободного электрона брать значение эффективной массы m*.
Условие применимости метода – медленное изменение потенциала возмущения W(r) по сравнению с периодическим потенциалом U(r), и то, что область локализации возмущения VR должна быть много больше постоянной решетки.
Применяется следующим образом:  ,
,
Подставляя вместо m0 à m*, U(r) = 0 (!), получаем следующее: 
2.10. В чем сходство и отличия модели Бора для атома водорода и Н-модели для донорных (акцепторных) состояний электрона (дырки) в примесных полупроводниках? Применимость Н-моделей.
Ответ:
Применимость вытекает из применимости метода m*, то есть когда применим метод m*, то применимы и Н-модели: см.2.9., rD>>a, rA>>a, rЭКС>>a, W(r)изменяется медленно по сравнению с U(r).
2.11. Что такое «экситоны» в кристалле по моделям Френкеля или Ваннье? Какая из этих концепций может быть рассчитана по Н-модели (водородоподобной модели) и как?
Ответ:
Квазичастица, состоящая из электрона и дырки, называется экситоном Ваннье-Мотта или экситоном большого радиуса. Размеры экситона Ваннье-Мотта велики по сравнению с периодом решетки твердого тела. Именно это обстоятельство позволяет с хорошим приближением рассматривать взаимодействие между электроном и дыркой как кулоновское взаимодействие двух точечных зарядов, ослабленное в e раз, где e - статическая диэлектрическая проницаемость кристалла.
Экситоном малого радиуса (экситоном Френкеля) называют связанное состояние электрона и дырки, находящихся на одном атоме или молекуле. Экситоны Френкеля обнаружены, в частности, в молекулярных кристаллах. Движение экситона Френкеля определяется передачей возбуждения от одного атома (или молекулы) к другому (другой). При этом радиус возбужденного состояния (радиус экситона Френкеля) примерно равен размеру атома. Итак, экситоны Ваннье-Мотта представляют собой связанные состояния электрона и дырки, которые могут находиться на разных узлах кристаллической решетки, а экситоны Френкеля можно представить себе как предельный случай экситонов Ваннье-Мотта, когда электрон и дырка находятся на одном и том же узле.
2.12. Когда в зонной структуре полупроводника появляются «примесные зоны», и каков количественный критерий их возникновения?
Ответ:
Примесь, вносящая отрицательное возмущение в поле решетки, приводит к появлению дискретного уровня энергии под дном зоны. Она является поставщиком электронов и называется донорной. Примесь, вносящая положительное возмущение, приводит к появлению дискретного уровня под потолком зоны. Она является поставщиком дырок и называется акцепторной.
Мелкие уровни энергии примеси качественно хорошо описываются Н-моделью. Энергия ионизации в таком случае равна: DЕD = 13,6×(mn*/m0)×1/e2, DEa = 13,52mP*/(e2m). Глубокие уровни можно описать с помощью экранирующего потенциала.

С ростом концентрации примеси дискретный уровень вследствие обменного взаимодействия расщепляется в примесную зону. Энергия ионизации примеси уменьшается.
С увеличением Nd, при достижении Nd критического, возникает перекрытие волновых функций Yk(r)донор.; Ndкрит = 1/rd3; rd = 0,52 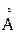 = 5,2*10-9, и локальные уровни энергии расщепляются в примесную зону.
= 5,2*10-9, и локальные уровни энергии расщепляются в примесную зону.
2.13. Чем отличаются свойства свободного электрона и электрона в идеальном кристалле?
Ответ:
В свободном пространстве электрон обладает p, m,e, r, v (p, r, v – векторы). Импульс можно выразить через волновой вектор k: p = hk, волна де Бройля Yk(r) = Аexp(ik,r), 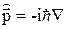 . В кристалле: законы сохранения не выполняются, поэтому вводится новый параметр для сохранения импульса и энергии – такой, что
. В кристалле: законы сохранения не выполняются, поэтому вводится новый параметр для сохранения импульса и энергии – такой, что  .
.
При переходе в кристалл волна де Бройля принимает вид: Yk(r) = Yk(r)exp(ik,r) à Yk(r) = j(k)exp(ik,r), а импульс становится квазиимпульсом: p à 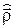 .
.
2.14. В чем основные положения теории «квазисвободного» электрона? Как она используется для построения зон Бриллюэна?
Ответ:
Основные положения: 1) Выбираем вид оператора возмущения Ŵ = U(r). 2) Ищем вид E(k) и Yk(r) в виде ряда: E(k)=E0(k)+E1(k)+E2(k)+…, для Yk(r) также. Состояния Yk(r) и E(k) вырожденные, если N различных значений Yk(r) соответствует одному значению Е(k). 3) Вдали от границ зоны Бриллюэна состояние Е(k) невырожденные, а на границе значение Е(k) двукратно вырожденные: E(k) = E(k + 2pb). 4) Делаются два приближения: первое: E(k) = E0+ <U(r)>,

второе: Поправка к энергии практически равна нулю, но есть вырожденные состояния, в которых энергия терпит разрыв, такие точки лежат на границе зон Бриллюэна.
Выводы: 1) Спектр электронов в кристалле – зонный (чередуются разрешенные и запрещенные зоны. 2) DЕразр(n+1) > DЕразр(n). Ширина запрещенной зоны растет с ростом номера n. 3) Чем выше номер зоны, тем больше кривизна закона дисперсии (т.е. уменьшается m*).
Из этой теории получается условие точек разрыва: k2 = k2 + 2pbk+4p2b2 à [b(k+pb)]=0 – это же является условием границ зон Бриллюэна.
2.15. В чем основные положения теории «квазисвязанного» электрона? Какие выводы этой теории используются для описания зонной структуры (например, валентной зоны или зоны проводимости Si)?
Ответ:
---------------------
2.16. В чем сходство и различие зонной структуры энергии электрона в Ge и Si?
Ответ:
Сходства: Прямая ГЦК, ОЦК – обратная, четыре валентных электрона, 3 подзоны (трехкратное вырождение), Evmax в точке Г, оба не прямозонные.
Отличия: Si: mL*=0,98m, mT*=0,19m, Ecmin находится внутри зоны, 6 долин, анизотропия изоэнергетической поверхности к = mL*/ mT* = 5,16, ширина запрещенной зоны DЕ = 1,08 эВ. Ge: mL*=1,58, mT*=0,082, Ecmin находится в точке L, 8 долин, анизотропия изоэнергетической поверхности к = 19,3, DЕ = 0,67 эВ.
2.17. Каковы общие особенности зонной структуры полупроводников АIIIВV или АII ВVI?
Ответ:
Общие особенности: Наличие двух минимумов – главного и побочного. С главных минимумов электроны могут перескакивать на побочные. В связи с этим увеличивается подвижность (m) и уменьшается проводимость (s). В зонах с малой эффективной массой быстро идет заполнение зоны проводимости.
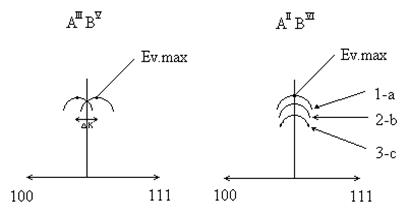
Отличие в валентной зоне АIII ВV и АII ВVI.
2.18. Как периодическое поле решетки кристалла изменяет свойства волновой функции и закона дисперсии электрона в идеальном кристалле в сравнении со свободным электроном?
Ответ:
Свободный электрон: Волновая функция - Y 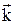
 - волна де Бройля;
- волна де Бройля;
Закон дисперсии: E = E(k) = h2k2/2m; U(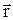 ) = 0; (- h2/2m)DY = EY; к – волновой вектор, направление движения волны. Е(к)= Е(-к) – свойство четности.
) = 0; (- h2/2m)DY = EY; к – волновой вектор, направление движения волны. Е(к)= Е(-к) – свойство четности.
Если электронная волна переходит в кристалл, то: Y (r) = j(r)exp(ik,r); j(r) = j (r+n); Y(r) = Yk(r) – волна Блоха.
В идеальном кристалле: Yk(r) = Yk(r)exp(ik,r); E(k) = E(k + 2pb)
Вывод: Если электрон из свободного пространства перенести в кристалл, то естественно ожидать, что воздействие периодического потенциала кристаллической решетки промодулирует амплитуду волновой функции электрона с периодом постоянной решетки, как это следует из соотношения: j(r) = j (r+n).
2.19. Какие изменения происходят в зонной структуре кристаллов при наличии дефектов (в зависимости от типа введенной примеси ее количества)?
Ответ:
При введении атома в качестве примеси в п/п, он вступает во взаимодействие с атомами основного вещества, поэтому энергия связи электрона примесного атома с собственным ядром уменьшается по сравнению с энергией связи электрона в свободном атоме. Примесь, вносящая отрицательное возмущение в поле решетки, приводит к появлению дискретного уровня энергии под дном зоны. Она является поставщиком электронов и называется донорной. Примесь, вносящая положительное возмущение, приводит к появлению дискретного уровня под потолком зоны. Она является поставщиком дырок и называется акцепторной.
2). Мелкие уровни энергии примеси качественно хорошо описываются Н-моделью. Энергия ионизации в таком случае равна: DЕD = 13,6×(mn*/m0)×1/e2. Глубокие уровни можно описать с помощью экранирующего потенциала.

3). С ростом концентрации примеси дискретный уровень вследствие обменного взаимодействия расщепляется в примесную зону. Энергия ионизации примеси уменьшается.
2.20. Какова связь между формой изоэнергетической поверхностью электрона в кристалле и его эффективной массой m*? Что такое ml и mn? Какие направления в зонах Бриллюэна в Ge или Si при этом выбираются?
Ответ:
В общем случае величина эффективной массы определяет форму изоэнергетической поверхности. Тензор m* в главных осях: m*= 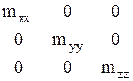 ; если m1=m2=m3, то Е(р) – является сферой. Если m1=m3=mt*, а m2=mL, то Е(р) – эллипсоид вращения, где mL- продольная составляющая m*, mt – поперечная составляющая m*. Если m1<m2, то вытянут вдоль оси вращения. Если m1>m2, то эллипс сжат вдоль оси вращения. Если m1¹m2¹m3, то эллипс имеет три разные оси. Чем сильнее различие m1, m2, m3, тем сильнее растянут эллипс. В Si – по направлению [100]. В Ge – вдоль оси [111].
; если m1=m2=m3, то Е(р) – является сферой. Если m1=m3=mt*, а m2=mL, то Е(р) – эллипсоид вращения, где mL- продольная составляющая m*, mt – поперечная составляющая m*. Если m1<m2, то вытянут вдоль оси вращения. Если m1>m2, то эллипс сжат вдоль оси вращения. Если m1¹m2¹m3, то эллипс имеет три разные оси. Чем сильнее различие m1, m2, m3, тем сильнее растянут эллипс. В Si – по направлению [100]. В Ge – вдоль оси [111].

2.21. Когда разрешенные зоны энергии для электрона (дырок) называют: «параболическими», «непараболичными», «сферическими», «простыми», «сложными», «многодоменными», «однодоменными»?
Ответ:
---------------
2.22. Чем отличаются сточки зрения «зонной теории» металлы, полупроводники, диэлектрики, полуметаллы?
Ответ:
Металлы - кристаллы, у которых валентная зона заполнена не полностью. Валентная зона выполняет роль сильно заполненной зоны проводимости.
Полупроводники – кристаллы, у которых валентная зона полностью заполнена, но следующая выше лежащая свободная зона отделена промежутком: DЕзапр » (2¸3) эВ.
Диэлектрики – кристаллы, у которых валентная зона заполнена полностью, но выше лежащая свободная зона отделена на величину > 3 эВ, тогда собственная проводимость отсутствует.
Полуметаллы – зонная структура такая же как у п/п, но минимум зоны проводимости лежит ниже максимума валентной зоны, т.е. разрешенные энергетические зоны перекрываются. Таким образом небольшое число состояний в зоне проводимости занято, а в валентной зоне свободно.
2.23. Какие полупроводники называют «прямозонными» или «непрямозонными»? Что такое DЕТ или DЕОПТ (термическая или оптическая ширина запрещенной зоны)? Приведите пример.
Ответ:
Если m* - тензор, и Есmin не находится в центре зоны Бриллюэна (нет сферической симметрии), то п/п – непрямозонный.
Если m* - скаляр, то п/п прямозонный. DЕт = термическая ширина запрещенной зоны, определяемая тепловым расширением и взаимодействием заряда с тепловыми колебаниями атомов решетки. DЕт = Е0 + aТ, где a - температурный коэффициент, a меньше 0 для определенного участка температуры. (табличн.). Если п/п прямозонный, то DЕ =DЕопт., где DЕопт – расстояние между: Еvmax и Еcmin.
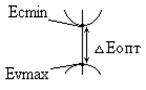
Примеры: Для Si - DЕопт = 3,4 эВ. Для АIII ВV: DЕт (Т) = 1,21 – 2,8*10-4 *Т эВ.
3-й модуль.
3.1. Запишите общий вид интегралов для подсчета концентраций электронов (дырок) в разрешенных зонах энергии и дайте их графическую интерпретацию для невырожденных полупроводников.
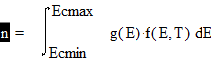 |
Ответ: Конц электронов в зоне проводимости можно представить в виде (формула1):
Где fФ-Д(E,T) – Ф-я Ферми - Дирека.
После преобразований получим выражение длы интеграла Ферми:
F1/2(h)= eh для -¥<h<-1 - для невырожденных п/п
F1/2(h)= eh/(0,27eh + 1) для -1<h<5 - слаб вырожд
F1/2(h)= 4h3/2/(3(p)1/2) для 5<h<¥ - для вырожд п/п и мет.
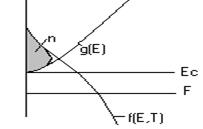
Граф интерприт формулы1 для конц электронов в невырожд п/п n-типа (площадь заштрих области пропорциональна конц электронов в зоне провод):
 |
Для дырок:
Где fp(E,T) – ф-я распределения дырок.
После преобразований получим выражение длы интеграла Ферми:
F1/2(-De-h)= e(-De-h) для -¥<(-De-h)<-1 - для невырожденных п/п
F1/2(-De-h)=e(-De-h)/(0,27 e(-De-h)+1) для -1<(-De-h)<5 -слаб вырожд
F1/2(-De-h)=4(-De-h)3/2/(3(p)1/2) для 5<h<¥ - для вырожд п/п и мет.
График строится аналог.
3.2. Какой полупроводник (или металл?) называют в статистике «вырожденным»? Когда это бывает?
Ответ: п/п наз полнастью вырожд, если уровень Ферми лежит внутри зоны энергии на расст не меннее 5кТ от экстремального значения энергии. В этом случае конц электронов(выше Ес) не зависит от Т. если ниже Еv на 5 кТ то ионизация дырок не зав от Т.
Вырождение наступ в результате сильного легирования п/п.
3.3. Что характеризует «уровень Ферми» в зонной диаграмме? Дайте все определения «уровня Ферми» (которые вы помните).
Ответ: 1). уровень ферми является нормированным параметром, характеризуемым числом электронов в единице объёма и плотностью энергетических состояний g(E), вычисляемой как число состояний, приход на единичный интервал изменения энергии.
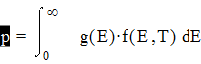 |
Величина энергии Ферми опред из условия, что число заполненых состояний при всех энергиях должно быть равно полному числу имеющихся электронов, т.е.
Где f(E,T) – ф-я Ферми – Дирека.
При Т=0 энергия Ф характеризует макс энергию частиц в системе. Таким образом, энергию Ф можно рассматривать как макс энергию частиц при Т=0.
2). Энергия Ф представляет термодинамический потенциал Гиббса, отнесённый к 1 частице, ее также называют хим потенциалом. Она опред приращение энергии с-мы частиц при увиличении числа частиц на 1. Поэтому энергия Ф определяется общим числом частиц. В п/п энергия Ф опред условием распред электронов по уровням энергий валентной зоны, зоны провод и дискретным уровням локализованных состояний. При Т=0 уровень ф лежит в серед запр зоны и с ростом Т он смещ к той зоне, в которой эффективная масса плотности состояний меньше.
3). Если постр график ф-и Ферми – Дирека, то уровень Ф - энергия, вероятность заполнения которой равен ½.
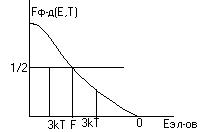 |
 |
3.4. Дайте количественную оценку ошибки от замены fФ-Д (Е, Т) » fМ-Б (Е, Т) для электронов (дырок).
Ответ:
Построив на одном графике ф-и Ф-Д и М-Б можно путём несложных вычислений найти, что при E-F=3kT разница меж ними менее 1%.
3.5. Что характеризует функция плотности состояний Nc(E) или Nv(E)? А эффективное число состояний NC или NV для электронов или дырок? Как их вычислить?
Ответ: N(E) равно числу состояний в единичном интервале энергии для единичного объёма кристалла, N(E) называют плотностью состояний.
Nc(E) – эффективное число состояний в зоне проводимости, приведённое к ее дну, т.е. к уровню Ec. Nc = 4,831*1015(m*dn/m0)3/2T3/2. Для Nv – аналог.
3.6. Каковы наиболее часто используемые формулы для приближенного расчета концентрации электронов (дырок) в невырожденных или вырожденных полупроводниках (металлах)?
Ответ: для невырожденного п/п: n(T) = (Nc*Nd/g)1/2e-DEd/2kT – облась ионизации примеси; n(T)=Nd – область истощения примеси; n(T)=ni(T)=(NcNv)1/2e-DEd/2kT – собственная ионизация. В общем случае n=NcF1/2(h), где F =
F1/2(h)= eh для -¥<h<-1 - для невырожденных п/п
F1/2(h)= eh/(0,27eh + 1) для -1<h<5 - слаб вырожд
F1/2(h)= 4h3/2/(3(p)1/2) для 5<h<¥ - для вырожд п/п и мет.
Для дырок аналогично.. p=NvF1/2(-De-h).
3.7. Как вводятся и что характеризуют параметры: «эффективная масса плотности состоянии», «тензор эффективной массы», «эффективная масса по заданному направлению»? Какая из этих величин определяет ход температурной зависимости уровня Ферми в полупроводниках?(F(T)=?-график)
Ответ: Эффективная масса электрона в кристалле m*=h2/(d2E/dk2). Тензор эффективной массы –
mxx mxy mxz
m*=(d2E/dP2)-1 => m*= myx myy myz<