Умножение на двузначные и трёхзначные числа.
Теоретическая основа:
· Приёмы письменного умножения на однозначное и круглое число;
· Распределительное свойство умножения (правило умножения числа на сумму);
· Приём письменного сложения столбиком.
1 .Повторяют все перечисленные вопросы.
2.На специальном уроке знакомятся с этим приёмом. Сначала изучают умножение на двузначное число. Рассмотрение случаев умножения на двузначное число полезно начать с устного приема, чтобы показать ход рассуждений:

Такая запись слишком сложная. Будем выполнять её столбиком:
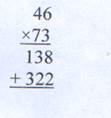
В ходе этих рассуждений подводим детей к выводу, что надо найти два неполных произведения и их сложить, то есть данное число умножаем на число десятков второго множителя; затем это число умножаем на число единиц второго множителя. Полученные результаты складываем. Если устно умножать трудно, лучше записать столбиком. Умножать начинаем с единиц. Показываем ход рассуждений при этом.
Умножаем 46 на 3, получим 138 единиц. Теперь умножим 46 на 70. Для этого умножаем 46 на 7 и полученное число умножим на 10, получаем 3220. Обращаем внимание, что 138 и 3220 - это неполные произведения. Число 3358 - полное произведение, или окончательный результат.
Обращаем внимание учащихся на то, что второе неполное произведение - это результат умножения на круглые десятки, поэтому всегда в нем на месте единиц стоит 0, его обычно не пишут. Это неполное произведение указывает на количество десятков в нем, его и начинают записывать под десятками первого неполного произведения.
Таким образом, рассуждения ведем так: 46 умножим на 3 единицы, получаем 138 единиц - первое неполное произведение. Теперь 46 умножим на 7 десятков, получаем 322 десятка - второе неполное произведение. Складываем.
и 4. Формирование умений и навыков.
При умножении на трехзначное число следует подвести детей к выводу, что рассуждения в принципе те же, только здесь будет добавляться только третье неполное произведение, а значит, третье слагаемое - какое-то количество сотен. Третье неполное произведение начинаем записывать под сотнями первого неполного произведения.
(Моро 4 класс 2 часть стр.44)
На данном уроке учащиеся знакомятся с умножением на двузначное число. Сначала повторяют устный приём умножения на двузначное число. Также, дается алгоритм действий.

(Моро 4 класс 2 часть стр.48)
На данном уроке учащиеся знакомятся с умножением на трёхзначное число. Предполагается, что учащиеся сами объяснят приём вычисления, так как знание свойства умножения числа на сумму и умение умножать на двузначные числа позволяют им самостоятельно открыть способ действия.

(Истомина 4 класс 1 часть стр.58-59)
В задании 154 учащиеся выясняют, значение каких произведений они уже умеют вычислять, а значение каких – не умеют. В задании 155 дети повторяют распределительное свойство умножения, а затем сравнивают записи и пытаются описать последовательность действий при умножении «в столбик» на двузначное число.


(Истомина 4 класс 1 часть стр.68)
В задании 183 учащиеся знакомятся с умножением на трёхзначное число.

(Аргинская 4 класс 1 часть стр.60)
В задании 118 составляется последовательность действий при умножении многозначного числа на двузначное число. В результате действия, выполняемые до сих пор при умножении многозначных чисел, получают новую форму — запись столбиком в отличие от подробной записи в строку.

(Аргинская 4 класс 1 часть стр.64)
В задании 126 устанавливается аналогия между умножением двузначных чисел на многозначные числа и трехзначных чисел друг на друга. При этом обращается внимание на особенности записи промежуточных результатов при умножении столбиком.

(Чекин 3 класс 2 часть стр.17)
В задании 34учащиеся знакомятся с основной идеей поразрядного способа умножения на двузначное число. Она основывается на правиле умножения числа на сумму. Формулировкой именно этого правила и должны завершить учащиеся выполнение этого задания.

(Чекин 3 класс 2 часть стр.19-20)
На данном уроке дети уже знакомятся с конкретной записью умножения на двузначное число столбиком.


Отдельной темы умножения на трёхзначное число по данной программе нет.