КУРСОВАЯ РАБОТА
по дисциплине
«Цифровая обработка сигналов»
Вариант №03
Выполнил: студент гр. Р/б-41-о
Голованов Никита Алексеевич
Защитил с оценкой_____________
Принял: асс. кафедры РТ
Снегур Дмитрий Александрович
Севастополь
СОДЕРЖАНИЕ
1. Задание №1......................................................................................................................... 3
2. Задание №2....................................................................................................................... 11
3. Задание №3....................................................................................................................... 18
4. Задание №4....................................................................................................................... 28
5. Задание №5....................................................................................................................... 38
Заключение.................................................................................................................................. 49
Библиографический список....................................................................................................... 50
ЗАДАНИЕ 1
Постановка задачи
Аналоговый сигнал x (t), изображенный на рис 1.1 длительностью T c = 1 мс подвергнут дискретизации путём умножения на последовательность δ-импульсов. Интервал дискретизации T Д. Амплитуда сигнала А равна номеру варианта V.
Номер варианта — A = 13 В.
Рис. 1.1 –– Исходный аналоговый сигнал
Требуется:
1) рассчитать спектр аналогового сигнала x (t) и построить график модуля спектральной плотности;
2) определить максимальную частоту в спектре аналогового сигнала fmax, ограничивая спектр по уровню 0,1 от максимального значения модуля спектральной плотности;
3) рассчитать интервал дискретизации T Д и число отсчетов дискретного сигнала N, которым он представляется на интервале [0, T с];
4) изобразить дискретный сигнал x д(nT Д), где n = 0, 1, … N –1 под аналоговым x (t) в том же временном масштабе;
5) определить спектральную плотность дискретного сигнала x д(nT Д) и построить график модуля спектральной плотности под графиком спектра аналогового сигнала в том же частотном масштабе;
6) провести дискретное преобразование Фурье (ДПФ) сигнала x д(nT Д), определить комплексные коэффициенты ДПФ и построить спектрограмму модулей этих коэффициентов под графиками спектров аналогового и дискретного сигналов в том же частотном масштабе;
7) сделать вывод о взаимосвязи спектров аналогового и полученного в результате его дискретизации дискретного сигналов.
Решение задачи
Для начала сформируем наш исходный аналоговый сигнал в программной среде MATLAB. Текст программы для выполнения этого задания:
clear all;
clc;
%Построение заданного аналогового сигнала
A = 03; Ts = 10^-3;
t = 0:Ts/1000:Ts;
for n=1:1:1001
s(n) = A*sin(pi*n*10^(-3));
end
figure(1)
plot(t,s)
ylim([0 13])
title('Исходный аналоговый сигнал')
xlabel('t, c')
ylabel('s(t)')
grid on
Построенный в программной среде MATLAB исходный аналоговой сигнал x (t), изобразим на рис. 1.2.
Рис. 1.2 –– Исходный аналоговый сигнал
Построим график модуля спектральной плотности и на уровне 0,1 от X (ω) max найдем fmax. Спектральная плотность рассчитывается по формуле (1.1)
(1.1)
Численный расчет спектральной плотности заданного сигнала x (t) можно выполнить методом трапеций с помощью функции MATLABtrapz (x, y). Напишем следующий текст программы:
f=-10000:1:10000;
fork=1:length(f)
x(k)=abs(trapz(t,s.*exp(-1i*2*pi*f(k)*t)));
y(k)=0.1*max(x);
end
figure(2)
plot(f,x,f,y)
title('Спектр аналогового сигнала')
xlabel('f, Гц')
ylabel('|S(jw)|')
grid on
График модуля спектральной плотности изобразим на рис. 1.3.
Рис. 1.3 –– Модуль спектральной плотности исходного сигнала
В этом случае fmax = 1,4 кГц. Воспользуемся теоремой Котельникова, чтобы найти минимальный период дискретизации
(1.2)
Подставляя числовые значения, получим:
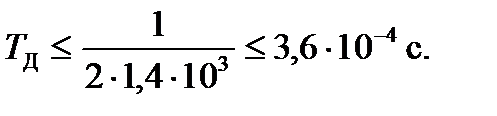
С учетом неравенства (1.2) выберем период дискретизации равный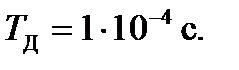 
Определим число отсчетов дискретного сигнала по формуле
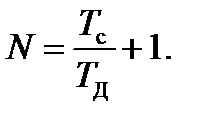(1.3)
Подставляя длительность сигнала и период дискретизации, получим следующее количество отсчетов:
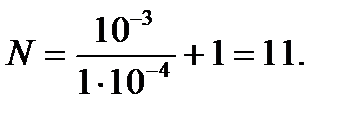
Построим и изобразим на рис. 1.4 дискретный сигнал x (nT Д). Напишем программу, соответствующую этому заданию:
Td = 1*10^-4;
N = Ts/Td+1
%Построение дискретного сигнала
t1 = 0:Td:Ts;
for n1=1:1:11
s1(n1) = A*sin(pi*(n1-1)*0.1);
end
figure(3)
stem(t1, s1)
title('Дискретныйсигнал')
xlabel('nTd, c')
ylabel('s(nTd)')
grid on
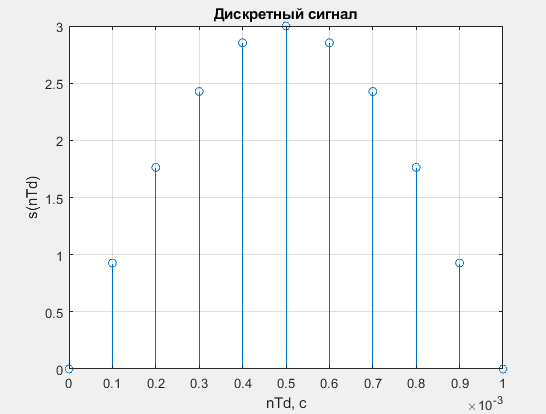
Рис. 1.4 –– Дискретный сигнал
Рассчитаем спектральную плотность дискретного сигнала с помощью формулы
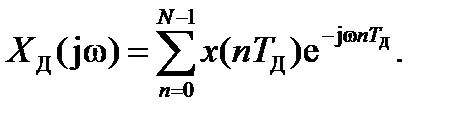(1.4)
Текст программы для этой операции укажем ниже:
%Определение спектральной плотности дискретного сигнала
f=-10000:1:10000;
for k=1:length(f)
x1(k)=abs(trapz(t1,s1.*exp(-i*2*pi*f(k)*t1)));
end
figure(4)
plot(f, x1)
title('Спектр дискретного сигнала')
xlabel('f, Hz')
ylabel('|S1(jw)|')
grid on
Изобразим график модуля спектральной плотности дискретного сигнала на
рис. 1.5.
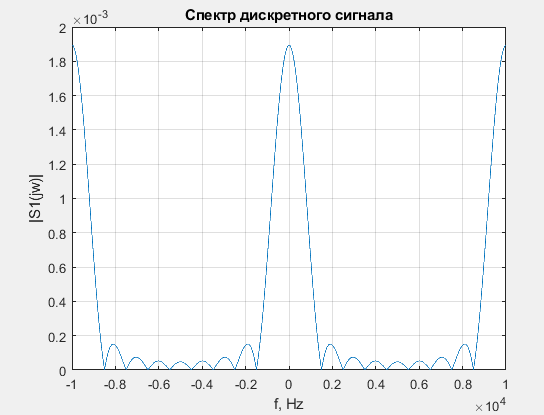
Рис. 1.5 –– Модуль спектральной плотности дискретного сигнала
Так как по теореме Котельникова f s ≥ 2 fmax, а мы выбрали частоту дискретизации
10 кГц, сделаем вывод, что наложение спектра отсутствует и это лучший случай для фильтрации. Однако выбрано слишком большое количество отсчетов и в реальных устройствах это будет занимать большее количество памяти в устройстве. Такая частота дискретизации была выбрана для удобства написания программы.
Дискретное преобразование Фурье определяется соотношением
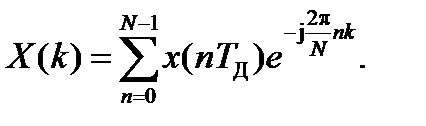(1.5)
В программном пакете MATLAB воспользуемся встроенной функцией fft. Отсчеты спектральной плотности следуют через интервалы
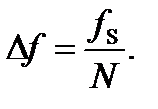(1.6)
Подставив значения, определим интервалы следования отсчетов спектральной плотности
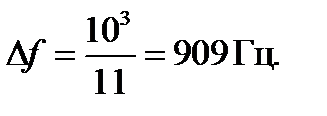
Напишем текст программы для нахождения дискретного преобразования Фурье:
%Выполнение дискретного преобразования Фурье
N=11;
fd = 10000;
n=0:1:10;
y=fft(s1);
figure(5)
Xm = abs(y);
Xmm = 2*abs(y)/N;
for j =1:1:22;
if j < 12
a(j) = Xmm(j);
else
a(j) = Xmm(j-N);
end
end
k = -11:1:10;
stem(k*fd/N,a)
title('МодуликоэффициентовДПФ')
xlabel('f, Hz')
ylabel('|S(k)|')
grid on
График модулей коэффициентов ДПФ представим на рис. 1.6.
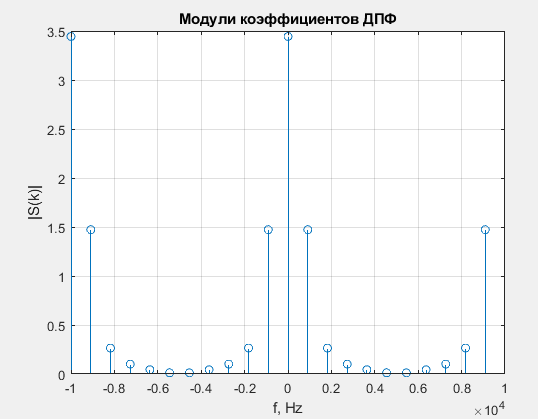
Рис. 1.6 –– Модули коэффициентов ДПФ
Выводы
1.3.1. Построен исходный аналоговый сигнал в программном пакете MATLAB (рис.1.2).
1.3.2. Построен график зависимости модуля спектральной плотности аналогового сигнала от частоты (рис. 1.3).
1.3.3. Определена максимальная частота в спектре аналогового сигнала f mах = 1,4 кГц путем ограничения спектра на уровне 0,1 от его максимального значения.
1.3.4. Рассчитан и выбран интервал дискретизации T Д = 10-4 с и число выборок
N = 11 за длительность сигнала T c =10-3 с. Такой интервал дискретизации был выбран для удобства написания программы в программном пакете MATLAB.
1.3.5. Построена дискретный сигнал, состоящий из N = 11 отсчетов (рис. 1.4).
1.3.6. Рассчитана зависимость модуля спектральной плотности дискретного сигнала от частоты, которая представляет собой непрерывную периодическую функцию частоты, с периодом равным частоте дискретизации f Д = 10000 Гц (рис. 1.5). Так как интервал дискретизации выбран в соответствии с теоремой Котельникова, то наложения спектров отсутствует.
1.3.7. Построена спектрограмма модулей нормированных коэффициентов ДПФ, из которой видно, что модули k -го и (N - k)-го коэффициентов равны между собой (рис. 1.6).
ЗАДАНИЕ 2
Постановка задачи
Дискретный сигнал, представленный последовательностью из восьми отсчетов имеет интервал дискретизации T Д = 10–3 с. Второе задание выполняется согласно номеру в списке (13 –– Требунский), укажем соответствующий заданию дискретный сигнал на рис. 2.1.
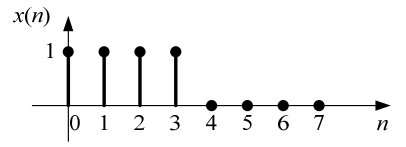
Рис. 2.1 –– Исходный дискретный сигнал
Требуется:
1) изобразить сигнальный граф алгоритма БПФ с прореживанием по времени для заданной последовательности;
2) используя сигнальный граф, вручную (не составляя программу) рассчитать комплексные спектральные коэффициенты для заданного дискретного сигнала;
3) изобразить на комплексной плоскости поворачивающие множители для каждой из стадий вычисления спектральных коэффициентов;
4) рассчитать модули и аргументы комплексных спектральных коэффициентов, по рассчитанным значения с использованием функций MATLAB построить графики спектральных характеристик;
5) составить скрипт MATLAB, в котором рассчитать модули и аргументы комплексных спектральных коэффициентов заданного сигнала с помощью функции fft, построить графики модуля и аргумента спектральной плотности, сравнить результаты ручного и программного расчетов;
6) рассчитать выигрыш БПФ в сравнении с алгоритмом ДПФ по числу операций комплексного умножения и сложения.
Решение задачи
Исходная 8-точечная последовательность имеет вид
x (n) = {0, 0, 1, 1, 0, 0, 1, 1}.
Разбиваем исходную 8-точечную последовательность x (n) на две 4-точечные последовательности x 0(n) и x 1(n), каждая из которых содержит соответственно четные и нечетные отсчеты последовательности x (n):
x 0(n) = {0, 1, 0, 1} и x 1(n) = {0, 1, 0, 1}.
На втором этапе прореживание последовательности x 0(n) разбивается на две 2-точечные последовательности x 00(n) и x 01(n), каждая из которых содержит соответственно четные и нечетные последовательности x 0(n):
x 00(n) = {0, 0} и x 01(n) = {1, 1}.
Последовательность x 1(n) на две 2-точечные последовательности x 10(n) и x 11(n), каждая из которых содержит соответственно четные и нечетные отсчеты последовательности x 1(n):
x 10(n) = {0, 0} и x 11(n) = {1, 1}.
Граф алгоритма БПФ с прореживанием по времени для заданной последовательности приведен на рис. 2.2.
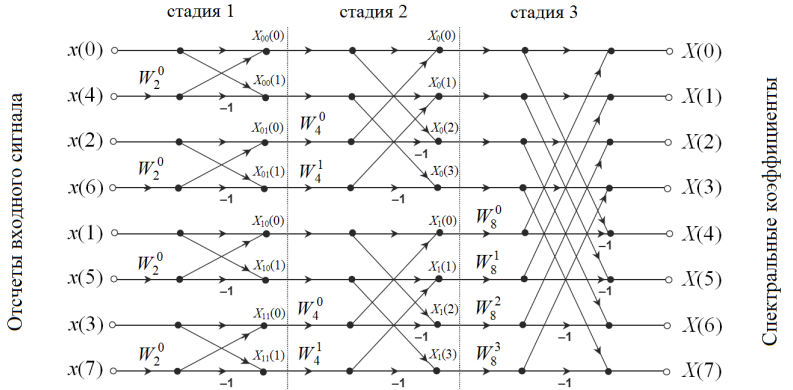
Рис. 2.2 –– Граф алгоритма БПФ с прореживанием по времени для заданной
последовательности
Определим поворачивающий множитель для каждой стадии по формуле
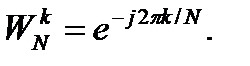(2.1)
Используем формулу Эйлера, чтобы перейти к тригонометрическим функциям для дальнейшего расчета
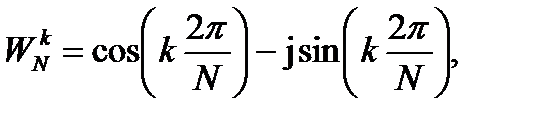(2.2)
где N — число отчетов в последовательности текущей стадии;
k — номер индексов текущей стадии, причем на первой стадии k = 0 для всех поворачивающих множителей, на второй стадии k = 0 и 1, на третьей стадии k = 0, 1, 2, 3.
Подставив числовые значения в формулу (2.1) получим следующее:
— для первой стадии: 
— для второй стадии: 
— для третей стадии: 
Поворачивающие множители на комплексной плоскости для всех стадий приведем на рис. 2.3.
Рис. 2.3 — Поворачивающие множители на комплексной плоскости для стадии 1 (а),
для стадии 2 (б) и для стадии 3 (в)
Определяем спектральные коэффициенты для последовательности 
:
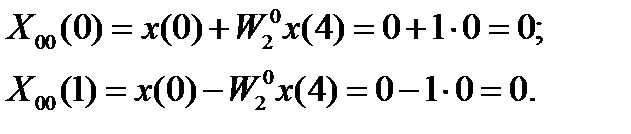
Определяем спектральные коэффициенты для последовательности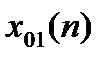 
:
Определяем спектральные коэффициенты для последовательности 
:
Определяем спектральные коэффициенты для последовательности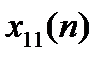 
:
В соответствии с операцией «бабочка», найдем спектральные коэффициентына второй стадии:
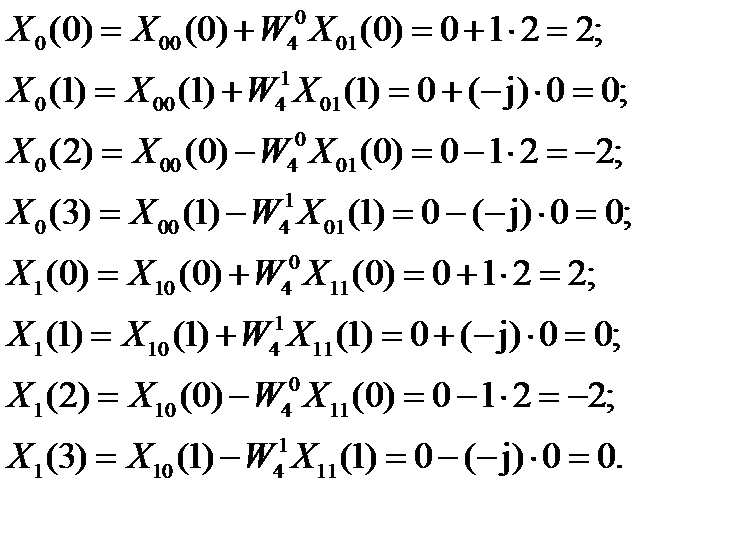
В соответствии с операцией «бабочка», найдем спектральные коэффициентына третьей стадии:
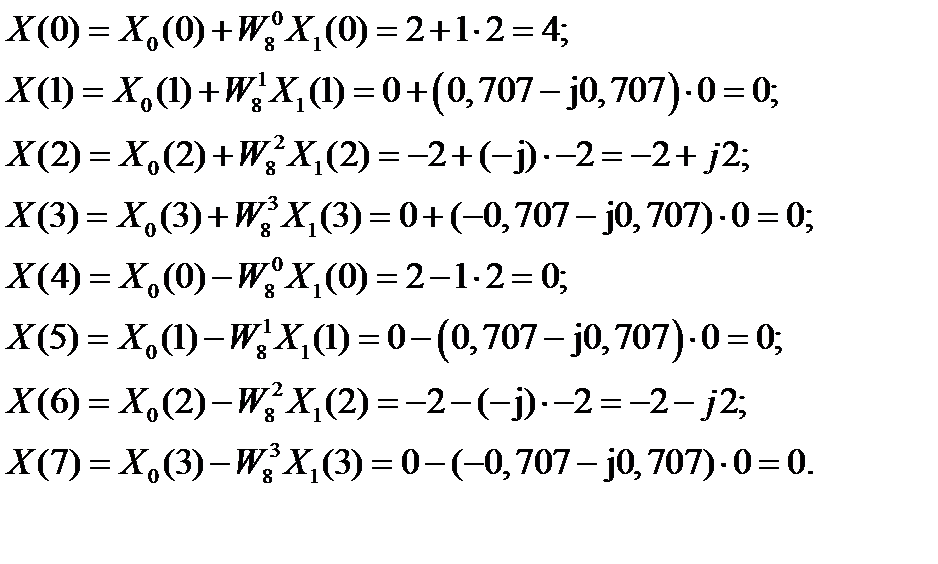
Модули и аргументы спектральных коэффициентов определяются по формуламсоответственно
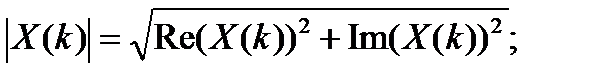(2.3)
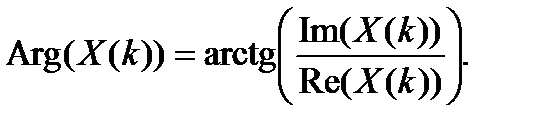(2.4)
Подставляя в формулы (2.3) и (2.4) значения спектральных коэффициентов, получим результаты, которые укажем в таблице 2.1.
| k | X (k) |
| -2+ j 2 | |
| -2- j 2 | |
Напишем листинг программы для определения БПФ, рассчитанного самостоятельно и с помощью функции fft:
clear all;
clc;
X = [4 1-2.414i 0 1-0.414i 0 1+0.414i 0 1+2.414i];
k = [0 1 2 3 4 5 6 7];
N = 8; fs = 10^3; f = k*fs/N;
figure(1)
subplot(2,1,1)
stem(f,abs(X))
title('Модули составляющих коэффициентов БПФ')
xlabel('f, Гц')
ylabel('|X(k)|')
grid on
subplot(2,1,2)
stem(f,angle(X))
title('Аргументы составляющих коэффициентов БПФ')
xlabel('f, Гц')
ylabel('Arg(X(k))')
grid on
x = [1 1 1 1 0 0 0 0];
Y = fft(x);
figure(2)
subplot(2,1,1)
stem(f,abs(Y))
title('Модули составляющих коэффициентов БПФ')
xlabel('f, Гц')
ylabel('|X(k)|')
grid on
subplot(2,1,2)
stem(f,angle(Y))
title('Аргументы составляющих коэффициентов БПФ')
xlabel('f, Гц')
ylabel('Arg(X(k))')
grid on
Графики зависимости модулей и аргументов от частоты, рассчитанные самостоятельно и при помощи функции fft,представлены на рис. 2.4––2.5.
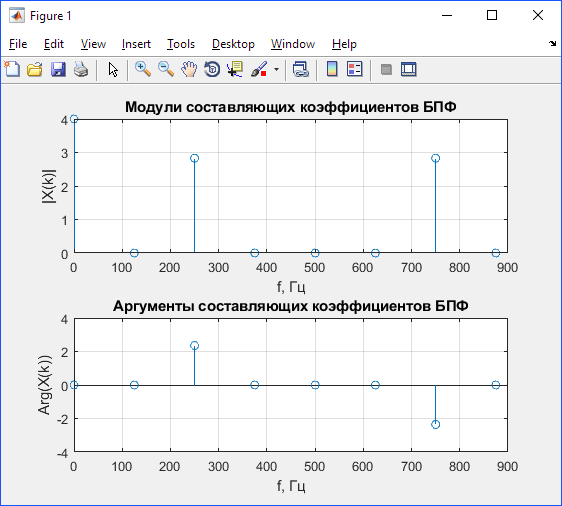
Рис. 2.4 –– Модули и аргументы коэффициентов БПФ, рассчитанных при помощи fft
Рис. 2.5 ––Модули и аргументы коэффициентов БПФ, рассчитанных самостоятельно
Найдем выигрыш БПФ относительно ДПФ по числу операций:
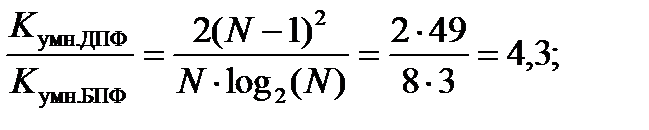
Выводы
2.3.1. Построен сигнальный граф 8-точечного алгоритма БПФ с прореживанием по времени для заданной последовательности (рис. 2.2). Из полученного графа видно, что базовая операция «бабочки» 2-точечного ДПФ формирует основу для всего вычисления спектральных коэффициентов. Вычисление осуществляется в три стадии. После того, как заканчивается вычисления на первой стадии, нет необходимости сохранять какие-либо предыдущие результаты. Результаты вычислений первой стадии могут быть сохранены в тех же самых регистрах или ячейках памяти, которые первоначально хранили отсчеты из временной области. Точно так же, когда заканчивается вычисления на второй стадии, результаты вычислений, полученные на первой стадии, могут быть удалены. Таким же образом осуществляется вычисления последнего каскада, заменяя в памяти промежуточный результат вычислений предыдущей стадии.
2.3.2. Рассчитаны и изображены на комплексной плоскости поворачивающие множители для каждой из стадий вычисления спектральных коэффициентов (рис. 2.3). Из данного рисунка видно, что на всех стадиях объединения число поворачивающих множителей удваивается, причем все множители предыдущей стадии объединения присутствуют и на следующей стадии. Таким образом, для того чтобы перейти к следующей стадии необходимо между поворачивающими множителями текущей стадии вставить поворачивающий множитель следующей стадии.
2.3.3. С использованием полученного сигнального графа, рассчитаны комплексные спектральные коэффициенты для заданного дискретного сигнала, определены их модули и аргументы. Также рассчитаны спектральные коэффициенты заданного сигнала с помощью MATLAB функции fft и построены графики спектральных характеристик данного сигнала (рис. 2.4––2.5). Сравнивая результаты самостоятельного расчета и расчета с помощью fft, видно, что они полностью совпадают. Идентичность графиков указывает на то, что БПФ не является приближенным алгоритмом. При отсутствии вычислительной погрешности он дает такой же результат, как и прямой метод ДПФ. Ускорение достигается исключительно за счет оптимизации вычислений.
2.3.4. Рассчитан выигрыш БПФ в сравнении с алгоритмом ДПФ по числу операций комплексного умножения и сложения. По результатам расчета можно сделать вывод, что БПФ позволяет значительно сократить время вычислений спектральных коэффициентов, в случае 8-точечной последовательности количество операций умножения уменьшается в
4,1 раза, а количество операций сложения — в 2,33 раза. Чем больше последовательность, тем больше будет выигрыш по числу операций, например, в 1024-точечной последовательности он будет составлять для умножения 204,4 раза, а для сложения –– 102,3 раза.
ЗАДАНИЕ 3
Постановка задачи
Цель работы:
Линейная дискретная система (ЛДС) задана разностным уравнением
(3.1)
где b 0, b 1, b 2, a 1, a 2 — коэффициенты, определяемые вариантом задания;
T Д = 1 мс –– интервал дискретизации сигналов.
Исходные данные для расчета представлены в таблице 3.1.
Требуется:
1. Составить структурную схему ЛДС.
2. На основе обобщенной передаточной функции рекурсивной ЛДС и заданных коэффициентов составить формулу передаточной функции ЛДС. Определить полюса передаточной функции и нанести их на р-плоскости. Сделать вывод об устойчивости ЛДС по положению полюсов на р -плоскости.
3. Составить формулу комплексной частотной характеристики, заданной ЛДС. Вывести соотношения для расчета АЧХ и ФЧХ заданной дискретной системы. Написать скрипт MATLAB, в котором, по полученным соотношениям, с помощью функции plot, построить графики АЧХ и ФЧХ заданной ЛДС. Построить те же графики с помощью
MATLAB -функции freqz. Сравнить полученные результаты и сделать выводы.
4. Составить системную функцию заданной ЛДС, определить полюса системной функции и нанести их на z -плоскости, сделать вывод об устойчивости.
5. Рассчитать и построить семь отсчетов импульсной характеристики ЛДС с учетом нулевых начальных условий;
6. Рассчитать и построить десять отсчетов выходного сигнала заданной ЛДС с нулевыми начальными условиями, если на её вход подаётся сигнал из задания №2.
Таблица 3.1 –– Исходные данные
| № | Коэффициенты разностного уравнения | ||||
| b 0 | b 1 | b 2 | a 1 | a 2 | |
| 0,6429 | -1,01 | 0,8 |
Решение
Структурная схема заданной ЛДС, составленная в соответствии с уравнением (3.1), представлена на рис. 3.1.
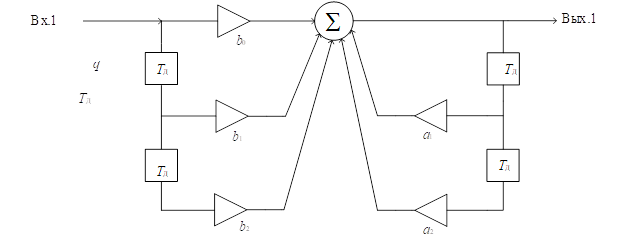
Рис. 3.1 –– Структурная схема заданной ЛДС
На основе обобщенной передаточной функции рекурсивной ЛДС и своих данных, напишем выражение в следующем виде
(3.2)
Для определения полюсов передаточной функции необходимо приравнять знаменатель (3.2) к 0
Корни этого уравнения будем считать в программном пакете MathCAD пошагово:
1) Замена -10-3 p=s;
2) Замена e s = x.
В итоге получим уравнение 
Проведя все расчеты с помощью функций Given и Find, вычислили два полюса. Ответы верны, так как после расчета была проведена проверка.
Тут будет график с расположением корней на плоскости.
Корни уравнения располагаются в левой полуплоскости, а это означает, что система устойчива.
Комплексные частотные характеристики ЛДС получим путем замены pна jω
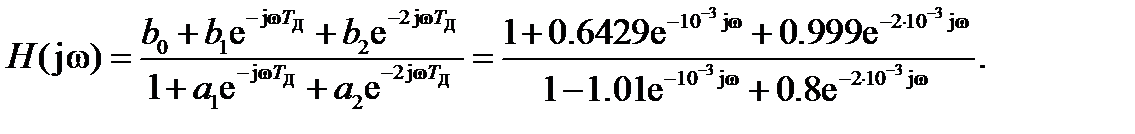(3.3)
Используя формулу Эйлера, представим выражение (3.3) в тригонометрической форме
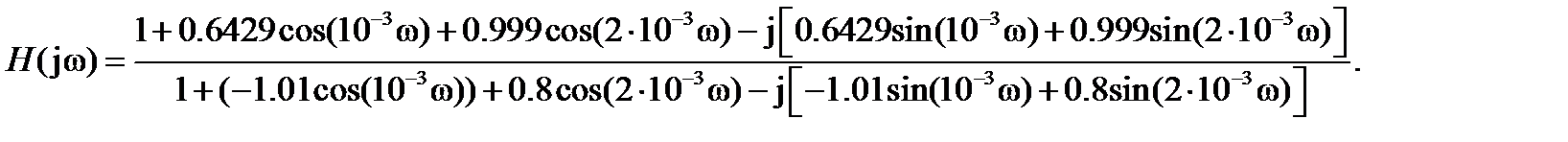(3.4)
Для получения АЧХ и ФЧХ найдем модуль и аргумент (3.4)
(3.5) 
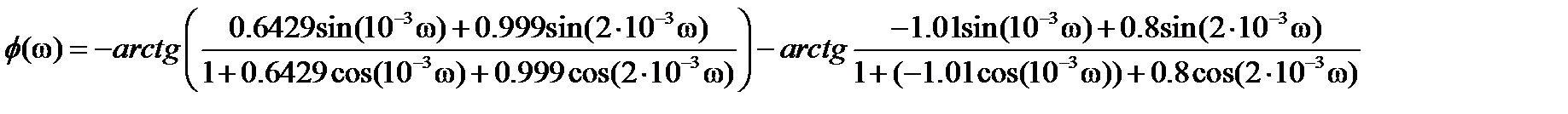(3.6)
По формулам (3.5––3.6) рассчитаем АЧХ и ФЧХ ЛДС в MATLAB, для этого напишем следующий листинг программы:
clear all;
clc;
b0=0; b1=-0.0208; b2=-0.0449; b3=-0.0706; b4=0.9045; b5=-0.0706; b6=-0.0449; b7=-0.0208; b8=0;
Td = 10^-3;
fd = 1/Td;
wd = 2*pi*fd;
f = 0:1/fd:fd/2;
for i=1:1:length(f)
H(i) = 20*log10(sqrt((b0+b1*cos(2*pi*f(i)*Td)+b2*cos(2*pi*2*f(i)*Td)+b3*cos(2*pi*3*f(i)*Td)+b4*cos(2*pi*4*f(i)*Td)+b5*cos(2*pi*5*f(i)*Td)+b6*cos(2*pi*6*f(i)*Td)+b7*cos(2*pi*7*f(i)*Td)+b8*cos(2*pi*8*f(i)*Td))^(2)+(b0+b1*sin(2*pi*f(i)*Td)+b2*sin(2*pi*2*f(i)*Td)+b3*sin(2*pi*3*f(i)*Td)+b4*sin(2*pi*4*f(i)*Td)+b5*sin(2*pi*5*f(i)*Td)+b6*sin(2*pi*6*f(i)*Td)+b7*sin(2*pi*7*f(i)*Td)+b8*sin(2*pi*8*f(i)*Td))^(2)));
end
figure(5)
subplot(2,1,1)
plot(f,H)
title('АЧХФВЧ')
ylabel('H(f), дБ')
xlabel('f, Гц')
grid on
for i=1:1:length(f)
F(i)=atan(-((b0+b1*sin(2*pi*f(i)*Td)+b2*sin(2*pi*2*f(i)*Td)+b3*sin(2*pi*3*f(i)*Td)+b4*sin(2*pi*4*f(i)*Td)+b5*sin(2*pi*5*f(i)*Td)+b6*sin(2*pi*6*f(i)*Td)+b7*sin(2*pi*7*f(i)*Td)+b8*sin(2*pi*8*f(i)*Td))/(b0+b1*cos(2*pi*f(i)*Td)+b2*cos(2*pi*2*f(i)*Td)+b3*cos(2*pi*3*f(i)*Td)+b4*cos(2*pi*4*f(i)*Td)+b5*cos(2*pi*5*f(i)*Td)+b6*cos(2*pi*6*f(i)*Td)+b7*cos(2*pi*7*f(i)*Td)+b8*cos(2*pi*8*f(i)*Td))));
end
subplot(2,1,2)
plot(f,F)
title('ФЧХФВЧ')
ylabel('F(f), рад')
xlabel('f, Гц')
grid on
Так как формула очень громоздкая и неудобная в описании, для достоверности построим АЧХ и ФЧХ ЛДС в программном пакете MathCAD. Результаты совпали, следовательно, ошибок не допущено. Результат работы программы в MATLAB изобразим на
рис. 3.2.
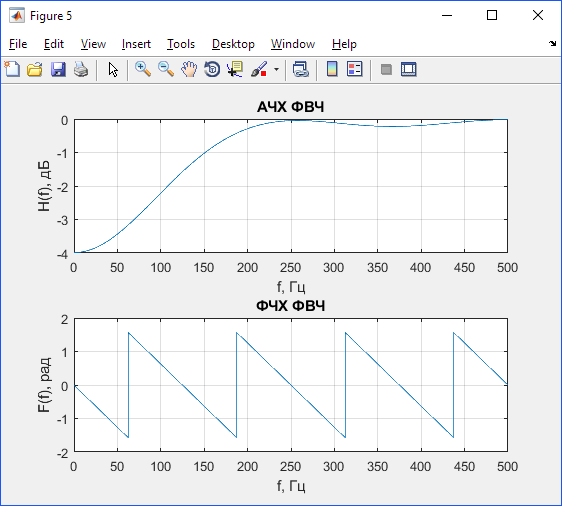
Рис. 3.2 –– АЧХ и ФЧХ ЛДС, рассчитанные по найденным формулам
Построим АЧХ и ФЧХ ЛДС, рассчитанные при помощи MATLAB -функции freqz, для этого напишем следующий листинг программы:
clear all;
clc;
Td = 10^-3;
fd = 1/Td;
wd = 2*pi*fd;
b0 = 1; b1 = 1.571; b2 = 1.008; a0 = 1; a1 = -0.97; a2 = 0.72;
b = [b0 b1 b2];
a = [a0 a1 a2];
w = -wd:1/fd:wd;
%Построние АЧХ и ФЧХ при помощи встроенной функции freqz
[H1, w1] = freqz(b,a, length(w), fd, 'whole');
figure(2)
subplot(2,1,1)
plot(w1,abs(H1))
xlim([0 fd/2])
title('АЧХЛДС')
ylabel('H(w)')
xlabel('f, Гц')
grid on
subplot(2,1,2)
plot(w1,unwrap(angle(H1)))
xlim([0 fd/2])
title('ФЧХЛДС')
xlabel('f, Гц')
ylabel('F(w), рад')
grid on
Результат работы программы укажем на рис. 3.3.
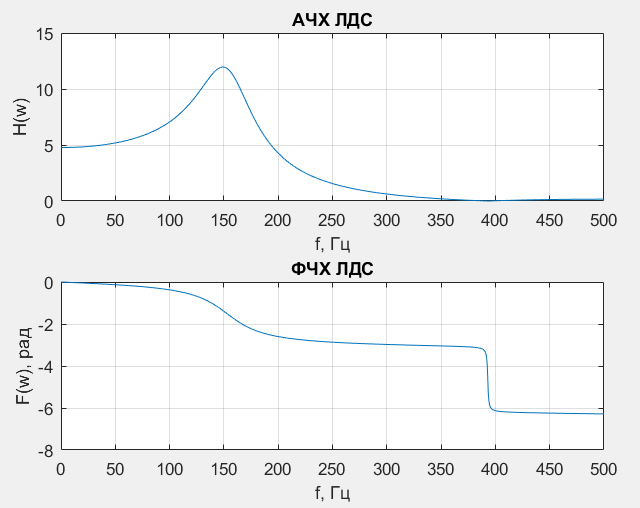
Рис. 3.3 –– АЧХ и ФЧХ ЛДС, рассчитанные про помощи функции freqz
Выражение для системной функции ЛДС найдем путем подстановки в формулу (3.2)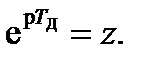 
В результате получим:
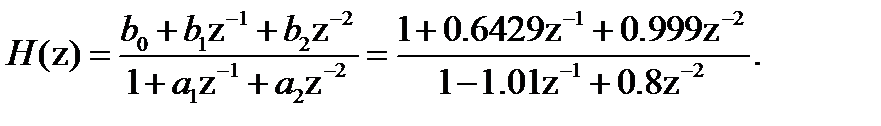(3.7)
Для проверки устойчивости системы воспользуемся следующим листингом программы:
b0=1; b1=0.6429; b2=0.999;
a0=1; a1=-1.01; a2=0.8;
bz=[b0 b1 b2]; az=[a0 a1 a2];
%Отображение диаграммы нулей и полюсов на z плоскости
figure(3)
zplane (bz, az)
legend('Нули','Полюса')
grid on
Получившуюся диаграмму нулей и полюсов изобразим на рис. 3.4.
Рис. 3.4 –– Диаграмма нулей и полюсов системной функции
Так как полюса находятся внутри единичной окружности, означает, что система устойчива.
Импульсная характеристика 
— это реакция дискретной системы на воздействие в виде функции Кронекера. Используя разностное уравнение, получаем
(3.8)
где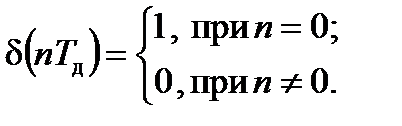 
Подставляя в выражение (3.8) известные значения, получаем результаты, представленные в таблице 3.2. Для расчета коэффициентов напишем следующий листинг программы:
for n = 1:1:8
if n == 1;
d(n) = 1;
else
d(n) = 0;
end
end
for n1=1:1:8
if n1 == 1
h1(n1) = b0*d(n1);
elseif n1 == 2
h1(n1) = b0*d(n1)+b1*d(n1-1)-a1*h1(n1-1);
else
h1(n1)= b0*d(n1)+b1*d(n1-1)+b2*d(n1-2)-a1*h1(n1-1)-a2*h1(n1-2);
end
end
figure(3)
subplot(2,1,1)
n1 = 0:1:length(h1)-1;
stem(n1*Td, h1)
title('ИмпульснаяхарактеристикаЛДС')
ylabel('h(t)')
xlabel('t, с')
grid on
[h,t] = impz(b,a)
figure(3)
subplot(2,1,2)
stem(t*Td, h)
xlim([0 7*Td])
title('Импульсная характеристика ЛДС')
ylabel('h(t)')
xlabel('t, с')
grid on
Результат работы программы изобразим на рис. 3.5.
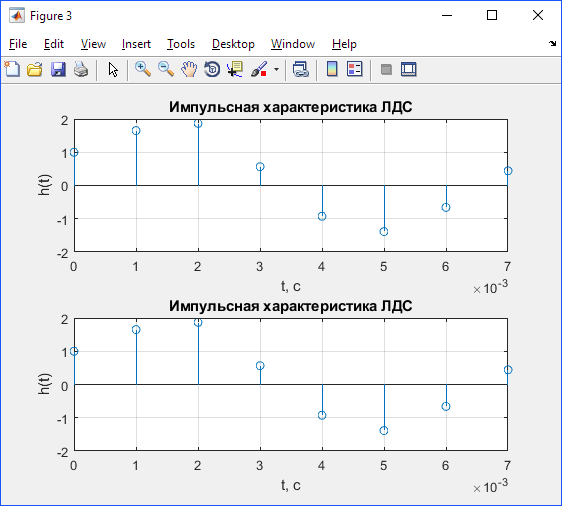
Рис. 3.5 –– Импульсная характеристика ЛДС с помощью расчета и функции impz
Таблица 3.2 –– Отсчеты импульсной характеристики
| n | ||||||||
| h (n) | 1.0000 | 1.6529 | 1.8684 | -0.5648 | -0.9243 | -1.3854 | -0.6598 | 0,4419 |
Так как нам нужно построить и рассчитать десять отсчетов выходного сигнала заданной ЛДС с нулевыми начальными условиями, если на её вход подаётся сигнал из предыдущего задания, а там дана 8-точечная последовательность, дополним её нулевыми отсчетами.Подставляя в выражение (3.1) известные значения, получаем результаты, представленные в таблице 3.3.
x (n) = {0, 0, 1, 1, 0, 0, 1, 1}.
Напишем следующий листинг программы:
x = [1 1 1 1 0 0 0 0 0 0];
for n2=1:1:10
if n2 == 1
y(n2) = b0*x(n2);
else
if n2 == 2
y(n2) = b0*x(n2)+b1*x(n2-1)-a1*y(n2-1);
else
y(n2)= b0*x(n2)+b1*x(n2-1)+b2*x(n2-2)-a1*y(n2-1)-a2*y(n2-2);
end
end
end
figure(4)
subplot(2,1,1)
n3 = 0:1:length(y)-1;
stem(n3*Td, y)
title('График реакции ЛДС на заданное воздействие')
ylabel('y(t)')
xlabel('t, с')
grid on
%Определение реакции ЛДС на входное воздействие при помощи функции filter
y1 = filter(b, a, x)
subplot(2,1,2)
n4 = 0:1:length(y1)-1;
stem(n4*Td, y1)
title('График реакции ЛДС на заданное воздействие')
ylabel('y(t)')
xlabel('t, с')
grid on
Результат работы программы изобразим на рис. 3.6.
Рис. 3.6 –– Реакция ЛДС на заданное воздействие с помощью расчета и функции filter
Таблица 3.3 –– Значения реакции ЛДС на заданное воздействие
| n | ||||||||||
| h (n) | 1,0000 | 3,5410 | 6,2938 | 7,1344 | 4,9679 | 0,6901 | -2,9075 | -3,3171 | -1,1242 | 1,2979 |
Выводы
3.3.1. Составлена структурная схема ЛДС (рис. 3.1). Из данной схемы видно, что заданная ЛДС представляет собой рекурсивный дискретный фильтр, так как 
3.3.2. Составлена формула передаточной функции ЛДС, определено, что полюса передаточной функции находятся в левой полуплоскости и, следовательно, система является устойчивой.
3.3.3. Найдены и построены АЧХ и ФЧХ ЛДС (рис. 3.2––3.3). Из полученных графиков видно, что частотные характеристики ЛДС, являются периодическими функциями частоты, с периодом равным частоте дискретизации. АЧХ, найденные аналитическим путем, совпали с частотными характеристиками, построенными при помощи MATLAB -функции. ФЧХ, найденные аналитическим путем и построенные при помощи MATLAB -функции не совпали, это может быть связано с иным методом расчета. MATLAB -функции, в некоторых случаях, не учитывают разрывы первого и второго рода.
3.3.4. Определена системная функция ЛДС, у которой полюса находятся внутри единичной окружности, следовательно, система устойчива (рис 3.4).
3.3.5. Построены восемь отсчетов импульсной характеристики ЛДС (рис. 3.5) и 10 отсчетов реакции ЛДС на заданное воздействие (рис. 3.6). Результаты, полученные прямой подстановкой заданных воздействий в разностное уравнение, совпали с результатами расчетов при помощи MATLAB -функций.
ЗАДАНИЕ 4
Постановка задачи
Цель работы:
Разработка и исследование нерекурсивного цифрового фильтра оконным методом. Исходные данные для расчета приведены в таблице 4.1.
Требуется:
а) вручную рассчитать отсчёты модифицированной окном импульсной характеристики нерекурсивного цифрового фильтра;
б) получить системную функцию цифрового фильтра;
в) рассчитать и построить АЧХ и ФЧХ цифрового фильтра;
г) составить структурную схему цифрового фильтра;
д) рассчитать и построить выходной сигнал фильтра, если на вход подаётся дискретный сигнал из задания 2 с частотой дискретизации этого задания.
Таблица 4.1 –– Исходные данные
| № варианта | Тип ЦФ | f Д, Гц | f з, Гц | f с, Гц | N | Оконная функция |
| ФВЧ | Бартлет |
Примечание.
В таблице приняты следующие обозначения:
–– f Д –– частота дискретизации;
–– f з –– частота полосы заграждения;
–– f с –– частота среза;
–– N –– порядок фильтра.
Решение
Рассчитаем отсчеты импульсной характеристики идеального ФНЧ по формуле
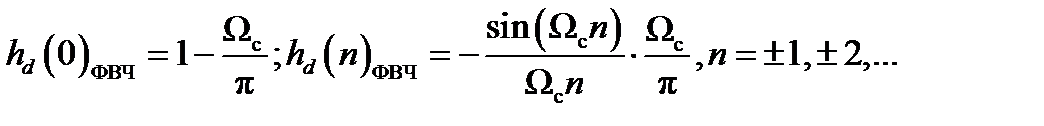, (4.1)
где 
.
Поставляя в формулу (4.1) известные значения, получим результаты, представленные в таблице 4.2.
Таблица 4.2 –– Отсчеты импульсной характеристики идеального ФВЧ
| n | –4 | –3 | –2 | –1 | |||||
| h d(n) | 0,074 | 0,083 | 0,089 | 0,094 | 0,9 | 0,094 | 0,089 | 0,083 | 0,074 |
Выражение, описывающее окно Бартлетта, имеет следующий вид
. (4.2)
Поставляя в формулу (4.2) известные значения получим результаты, представленные в таблице 4.3.
Таблица 4.3 –– Значение отсчетов окна Бартлетта
| n | |||||||||
| w (n) | 0,25 | 0,5 | 0,75 | 0,75 | 0,5 | 0,25 |
Рассчитаем, взвешенные окном Бартлетта, отсчеты физически реализуемой импульсной характеристики ФНЧ по формуле
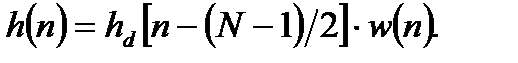, (4.3)
Поставляя в формулу (4.3) известные значения получим результаты, представленные в таблице 4.3.
Таблица 4.3 –– Значение отсчетов окна Бартлетта
| n | |||||||||
| h (n) | 0,02 | 0,04 | 0,07 | 0,9 | 0,07 | 0,04 | 0,02 |
Для построения графиков исходной импульсной характеристики, смещенной вправо на 5 отсчета, окна Бартлетта и взвешенной окном Бартлетта импульсной характеристики напишем следующий листинг программы:
clc;
clear all;
fd = 1000; fz = 50; fs = 150; N = 9;
%норм работа фильтра N=15; fs=100; k==8; k-8;
Ws = 2*fs/fd
for k = 1:1:N
if k==5
hd(k)=1-Ws/pi;
else
hd(k) = (-Ws/pi)*sin(Ws*(k-5))/(Ws*(k-5))
end
end
w = bartlett(N)
for k = 1:1:N
h(k) = hd(k)*w(k)
end
figure(2)
n1 = 0:1:length(h)-1;
stem(n1, hd)
title('Отсчеты исходной импульсной характеристики ФВЧ, смещенной в право на 5 отсчетов')
ylabel('hd(n)')
xlabel('n')
grid on
figure(3)
n1 = 0:1:length(w)-1;
stem(n1, w)
title('ОтсчетыокнаБартлетта')
ylabel('w(n)')
xlabel('n')
grid on
figure(4)
n1 = 0:1:length(h)-1;
stem(n1, h)
title('Отсчеты полученной импульсной характеристики ФВЧ')
ylabel('h(n)')
xlabel('n')
grid on
b1 = fir1(N-1, Ws, 'high', w, 'noscale');
%Расчет и построение частотных характеристик ФНЧ
[H1, w1] = freqz(b1, 1, 10000, fd, 'whole');
figure(1)
subplot(2,1,1)
plot(w1, 20*log10(abs(H1)))
xlim([0 fd/2])
title('АХЧФВЧ')
ylabel('H(f), дБ')
xlabel('f, Гц')
grid on
subplot(2,1,2)
plot(w1, unwrap(angle(H1)))
xlim([0 fd/2])
title('ФЧХФВЧ')
ylabel('F(f), рад')
xlabel('f, Гц')
grid on
%Определение реакции фильтра на заданной воздействие
figure(6)
x = [0 0 1 1 0 0 1 1]
y = conv(x, b1);
n2 = 0:1:length(y)-1;
stem(n2, y)
title('Реакция ФВЧ на заданное воздействие')
ylabel('y(n)')
xlabel('n')
grid on
Результат работы программы приведем на рис. 4.1––4.3.
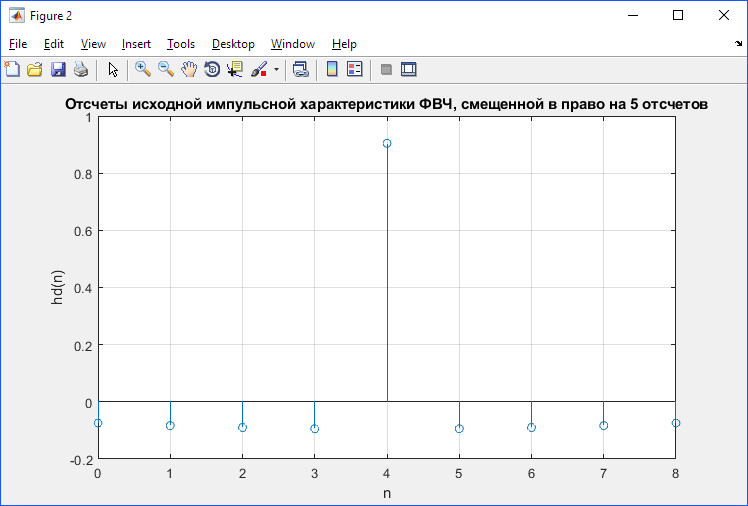
Рис. 4.1 –– Отсчеты импульсной характеристики ФВЧ, смешенной в право
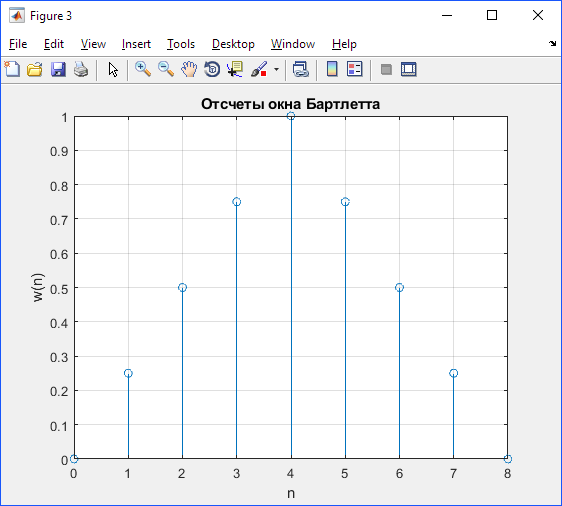
Рис. 4.2 –– Отсчеты окна Бартлетта
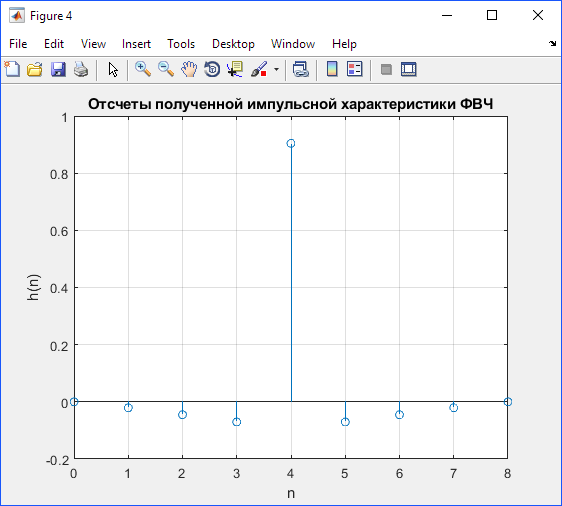
Рис. 4.3 –– Отсчеты импульсной характеристики, обработанной окном Бартлетта
Так как проектируемый фильтр является нерекурсивным, то коэффициенты системной функции равны отсчетам импульсной характеристики.
Выражение для системной функции нерекурсивного цифрового фильтра имеет вид
, (4.4)
Подставляя в формулу (4.4) известные значения, получаем:
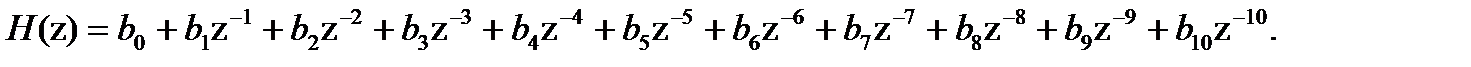(4.5)
Найдем выражения для АЧХ и ФЧХ комплексной частотной характеристики, для этого заменим z - n на e-j wnT d, после чего перейдем к тригонометрической форме комплексного числа с помощью формулы Эйлера
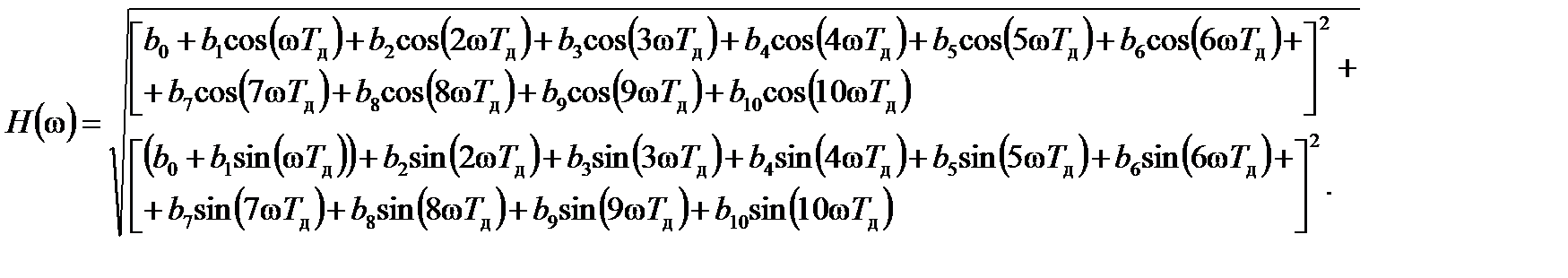
Построим АЧХ и ФЧХ с помощью (4.6––4.7). Напишем следующий листинг программы:
clearall;
clc;
b0=0; b1=0.007; b2=0.029; b3=0.062; b4=0.089; b5=0.1; b6=0.089; b7=0.062; b8=0.029; b9=0.007; b10=0;
Td = 10^-3;
fd = 1/Td;
wd = 2*pi*fd;
f = 0:1/fd:fd/2;
for i=1:1:length(f)
H(i) = 20*log10(sqrt((b0+b1*cos(2*pi*f(i)*Td)+b2*cos(2*pi*2*f(i)*Td)+b3*cos(2*pi*3*f(i)*Td)+b4*cos(2*pi*4*f(i)*Td)+b5*cos(2*pi*5*f(i)*Td)+b6*cos(2*pi*6*f(i)*Td)+b7*cos(2*pi*7*f(i)*Td)+b8*cos(2*pi*8*f(i)*Td)+b9*cos(2*pi*9*f(i)*Td)+b10*cos(2*pi*10*f(i)*Td))^(2)+(b0+b1*sin(2*pi*f(i)*Td)+b2*sin(2*pi*2*f(i)*Td)+b3*sin(2*pi*3*f(i)*Td)+b4*sin(2*pi*4*f(i)*Td)+b5*sin(2*pi*5*f(i)*Td)+b6*sin(2*pi*6*f(i)*Td)+b7*sin(2*pi*7*f(i)*Td)+b8*sin(2*pi*8*f(i)*Td)+b9*sin(2*pi*9*f(i)*Td)+b10*sin(2*pi*10*f(i)*Td))^(2)));
end
figure(5)
subplot(2,1,1)
plot(f,H)
title('АЧХФНЧ')
ylabel('H(w), дБ')
xlabel('f, Гц')
grid on
for i=1:1:length(f)
F(i)=atan(-((b0+b1*sin(2*pi*f(i)*Td)+b2*sin(2*pi*2*f(i)*Td)+b3*sin(2*pi*3*f(i)*Td)+b4*sin(2*pi*4*f(i)*Td)+b5*sin(2*pi*5*f(i)*Td)+b6*sin(2*pi*6*f(i)*Td)+b7*sin(2*pi*7*f(i)*Td)+b8*sin(2*pi*8*f(i)*Td)+b9*sin(2*pi*9*f(i)*Td)+b10*sin(2*pi*10*f(i)*Td))/(b0+b1*cos(2*pi*f(i)*Td)+b2*cos(2*pi*2*f(i)*Td)+b3*cos(2*pi*3*f(i)*Td)+b4*cos(2*pi*4*f(i)*Td)+b5*cos(2*pi*5*f(i)*Td)+b6*cos(2*pi*6*f(i)*Td)+b7*cos(2*pi*7*f(i)*Td)+b8*cos(2*pi*8*f(i)*Td)+b9*cos(2*pi*9*f(i)*Td)+b10*cos(2*pi*10*f(i)*Td))));
end
subplot(2,1,2)
plot(f,F)
title('ФЧХФНЧ')
ylabel('F(w), рад')
xlabel('f, Гц')
grid on
Построим АЧХ и ФЧХ с помощью MATLAB -функции freqz. Напишем следующий листинг программы:
b1 = fir1(N-1, Ws, w, 'noscale');
%Расчет и построение частотных характеристик ФНЧ
[H1, w1] = freqz(b1, 1, 10000, fd, 'whole');
figure(1)
subplot(2,1,1)
plot(w1, 20*log10(abs(H1)))
xlim([0 fd/2])
ylim([-150 10])
title('АХЧФВЧ')
ylabel('H(w), дБ')
xlabel('f, Гц')
grid on
subplot(2,1,2)
plot(w1, unwrap(angle(H1)))
xlim([0 fd/2])
title('ФЧХФВЧ')
ylabel('F(w), рад')
xlabel('f, Гц')
grid on
Результат работы программы покажем на рис. 4.4–4.5.
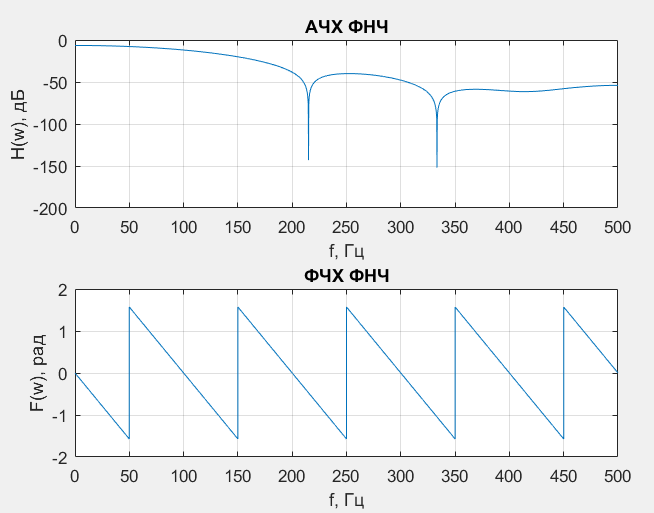
Рис. 4.4 –– АЧХ и ФЧХ, построенные с помощью (4.6––4.7)
Рис. 4.