Определение.
Сфера (поверхность шара) — фигура, образованная вращением полуокружности вокруг своего диаметра.
Определение.
Шар — фигура, полученная вращением полукруга вокруг диаметра, ограничивающего этот полукруг.
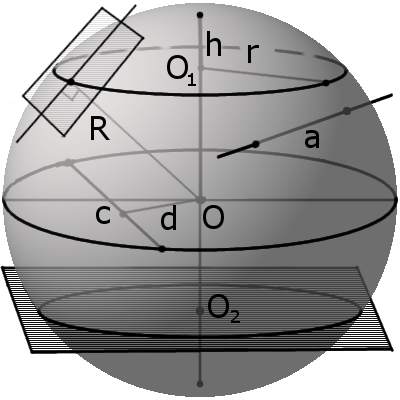
Определение. Радиус сферы (шара) (R) - это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).
Определение. Диаметр сферы (шара) (D) - это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.
Формула. Площадь поверхности шара через радиус или диаметр:
S = 4πR2 = πD2
Секущая, хорда, секущая плоскость сферы и их свойства
Определение. Секущая сферы - это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.
Определение. Хорда сферы (шара) - это отрезок, соединяющий две точки сферы (поверхности шара).
Определение. Секущая плоскость - это плоскость, которая пересекает сферу.
Теорема 11. Всякое сечение шара плоскостью есть круг, центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.
Определение. Диаметральная плоскость - это секущая плоскость, проходящая через центр сферы или шара, сечение образует соответственно большую окружность и большой круг. Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).
Теорема 12. Всякое сечение сферы плоскостью есть окружность. Центр этой окружности есть основание перпендикуляра, опущенного из центра сферы на секущую плоскость.
Любая хорда, проходящая через центр сферы (шара) является диаметром.
Хорда является отрезком секущей прямой.
Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:
d <R
Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m <R
Определение. Полусфера (полушар) - это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.
Касательная, касательная плоскость к сфере и их свойства
Определение. Касательная к сфере - это прямая, которая касается сферы только в одной точке.
Определение. Касательная плоскость к сфере - это плоскость, которая соприкасается со сферой только в одной точке.
Теорема 13. Плоскость, перпендикулярная к радиусу шара (сферы) в его внешнем конце, является касательной к этому шару (сфере).
Теорема 14. Каждая касательная к сфере плоскость перпендикулярна к радиусу этой сферы, проведенному к точке касания.
Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.
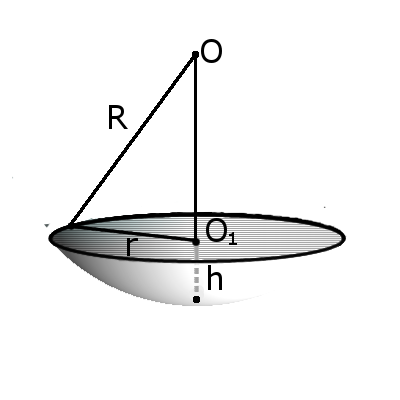
Определение. Сегмент шара - это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Формула. Площадь внешней поверхности сегмента шара с высотой h через радиус шара R:
S = 2πRh

Определение. Шаровым поясом (слоем) - это часть шара, которая образуется в результате его сечения двумя параллельными плоскостями и находится между ними.
Формула. Площадь внешней поверхности шарового пояса с высотой h через радиус шара R:
S = 2πRh
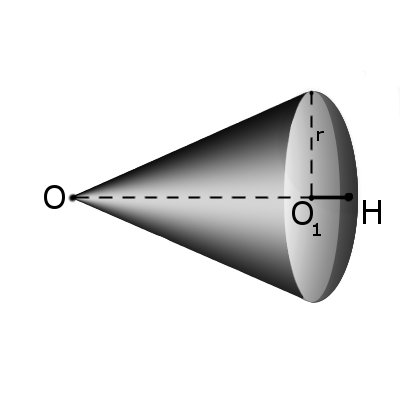
Определение. Шаровым сектором называется фигура, полученная при вращении кругового сектора с углом, меньшим 90, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов.