Если в пространстве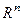 
даны 2 подпространства размерности 
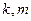соответственно (с помощью систем векторов 
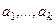и 
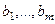), то для нахождения пересечения подпространств нужно составить и решить систему: 
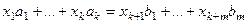. Перенесём слагаемые справа налево, и в итоге увидим, что это - именно однородная система:
.
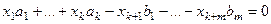Решая её, получим ФСР, затем нужно будет составить линейные комбинации векторов 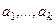или 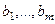с помощью найденных 
.
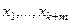Задача 1. В трёхмерном пространстве заданы два 2-мерных подпространства, с помощью систем векторов:
, 
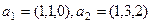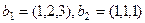. Найти базис их пересечения.
Решение.
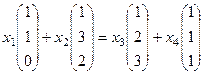
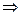
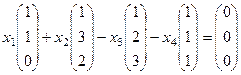
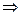однородная система уравнений 
.
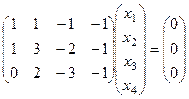Преобразуем основную матрицу методом Гаусса.
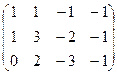
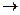
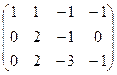
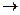
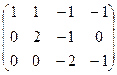
базисный минор в первых трёх столбцах, свободная переменная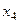 
.
Из последнего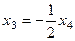 
, из 2-го 
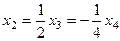. Тогда из 1-го
= 
= 
.
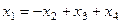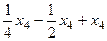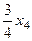Общее решение: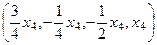 
. ФСР: 
.
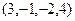Пересечение одномерно. Если посчитаем линейную комбинацию векторов 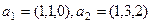с коэффициентами 
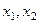, либо
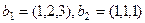с коэффициентами 
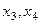, получим одно и то же:
Подставить в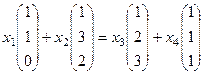
, 
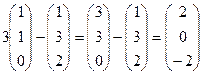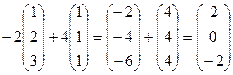
Можно сократить на 2 и в качестве базиса можно принять вектор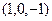 
. Ответ. базис пересечения: .
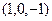Пересечение может оказаться и 2-мерным, то есть 2 указанные плоскости совпадать. Посмотрим, как это влияет на решение, увидим из следующего примера.
Задача 2. В трёхмерном пространстве заданы два 2-мерных
подпространства, с помощью систем векторов:
, 
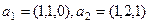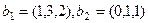. Найти базис их пересечения.
Решение. Строим систему уравнений, как и в прошлой задаче.
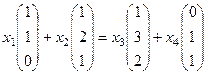
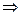
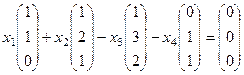
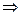однородная система уравнений 
.
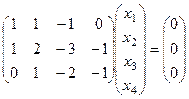Преобразуем основную матрицу методом Гаусса.
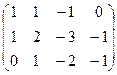
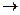
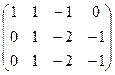
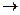
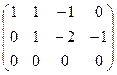
Третье уравнение состоит из нулей, ранг системы равен 2.
Из второго,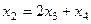 
, тогда из 1-го
= 
= 
.
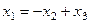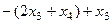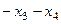Общее решение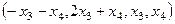 
,
ФСР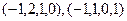 
.
Подставим в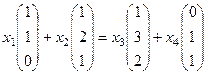
, 
.
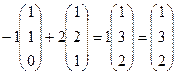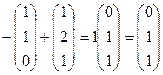Таким образом, 2 вектора второй системы получились базисом пересечения. Плоскости совпадают.
|
|
Задача 3. Найти базис пересечения двух трёхмерных подпространств 4-мерного пространства.
,
.
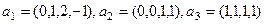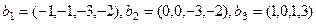Решение.
,
,
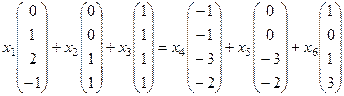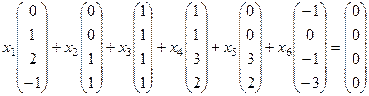Строим и преобразуем основную матрицу.
,
= 
.
= 
= 
.
= 
= 
.
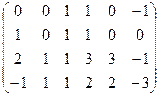
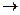
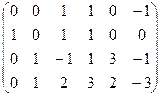
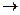
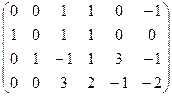
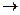
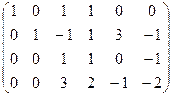
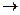
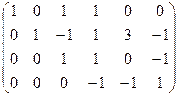
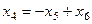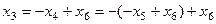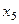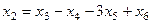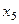
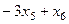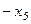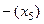
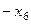Общее решение: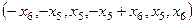 
.
ФСР: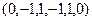 
, 
.
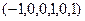Подставляем в
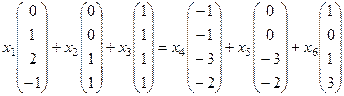
1) 
,
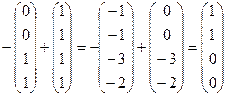2) 
.
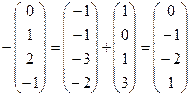Ответ. Базис пересечения: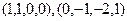 
.
ПРАКТИКА 2. 13.2.2021.
Нахождение определителей Грама для систем функций.
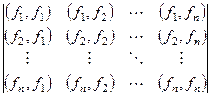, где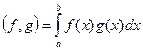 
Каждое х как координата, континуум координат.
Матрица Грама невырождена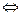 
система функций ЛНС.
Задача 1 (а,б).
а) Даны две функции на (0,1):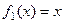 
, 
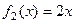. (ЛЗС)
б) Даны две функции на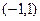 
:
, 
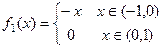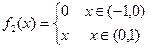. (ЛНС)
Найти определители Грама этих систем.
а)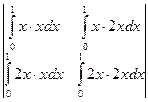 
= 
= 
=
= 
.
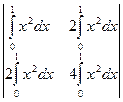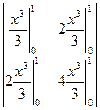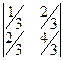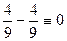б)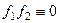 
, значит, и интеграл от 
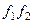равен 0.
= 
= 
.
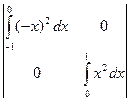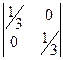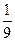Задача 2 (комбинированная, на поиск пересечения и проекции).
Даны два подпространства, с помощью линейных оболочек систем векторов:
,
.
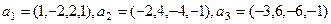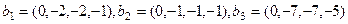Найти базис их пересечения, и проекцию вектора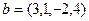 
на пересечение.
Решение. Составляем выражение:
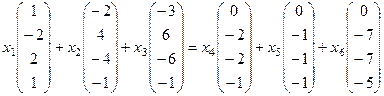
Переносим в левую часть:
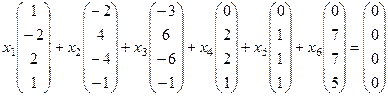
Решаем однородную систему с такой основной матрицей:
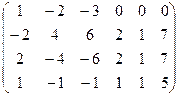
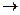
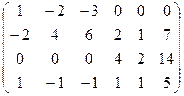
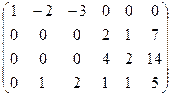
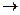
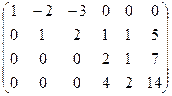
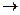
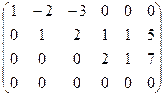
Ранг 3. Базисный минор можно составить из 1,2,5 столбцов, чтобы коэффициенты по возможности были 1.
Система:
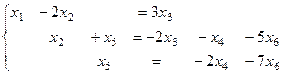
Из третьего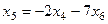 
,
Тогда из второго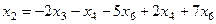 
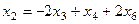
Из первого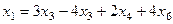 
, 
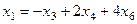
Общее решение
.
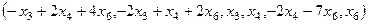ФСР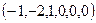 
, 
, 
.
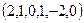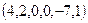Каждое подставить в
.
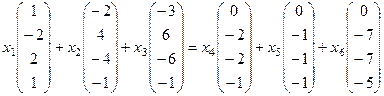
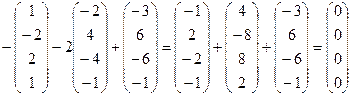
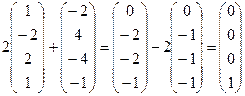
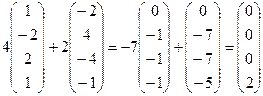Итак, получили векторы (0,0,0,0), (0,0,0,1), (0,0,0,2).
То есть, пересечение одномерно, базис (0,0,0,1).
Проекция вектора 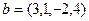на а = (0,0,0,1), это последняя координата, то есть 4.
Либо по формуле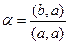 
то же самое.