Расчетно-графическая работа
По дисциплине «Теоретические основы электротехники»
«Расчет переходных процессов в линейных электрических цепях».
Вариант № ХХ.
Выполнил студент гр. АП-03-1
???????????.
Проверил доцент кафедры, к.т.н. Иванов Г.В.
Магнитогорск
2005 г
Содержание:
Расчет переходных процессов в цепи с постоянным источником ЭДС………3
Классический метод……………………………………………………….…..3
Операторный метод…………………………………………………………...7
Расчет переходных процессов в цепи при синусоидальном источнике напряжения………………………………………………………………………12
Расчет переходных процессов в цепи с постоянным источником ЭДС.
Параметры цепи: E=200B, c=20 мкФ, L=1мГн, R1=6Ом, R2=3Ом, R3=2Ом
Классический метод.
1. Составление характеристического уравнения. Сопротивление Z(p) эквивалентное относительно источника после коммутации, находим по формуле, приняв катушку за элемент сопротивления pL, а конденсатор 1/pC.
Заменив 
на R и приравняв Z(p) к нулю, находим корни полученного уравнения:
Корни действительные, свободная составляющая запишется в виде:
Вследствие равенства и равенства емкостей конденсаторов вид переходных процессов на них будет одинаков.
2. Переходные функции ищем в виде:
3. Определение начальных условий. Ток в катушке и напряжение на конденсаторе до коммутации, согласно основным законам коммутации скачком изменится не могут т.е
iL(-0)= iL(+0)
uc(-0)= uc(+0)
Учитывая это и то, что в начальный момент ключ был разомкнут, получим:
Расчет uL(+0) и ic (+0) произведем на основе законов Кирхгофа в схеме после коммутации для момента времени t=+0
4. Расчет принужденных значений токов и напряжений в установившемся после коммутации режиме, исходя из того, что при постоянном токе емкость – обрыв, а катушка – короткое замыкание:
5. Определение постоянных интегрирования. Подставим начальные условия и принужденные составляющие в уравнения пункта 2 при t=0:
6. Представление искомых переходных функций.
Отыскав постоянные интегрирования, и определив вид свободной составляющей, запишем полученные зависимости iL(t), uL(t), ic(t), uc(t) и i1(t).
Операторный метод.
Сущность операторного метода состоит в следующем. По формуле прямого преобразования Лапласа
находятся изображения токов I(p) и действующих напряжений.
Затем с помощью обратного преобразования Лапласа
осуществляется переход от изображения I(p) к оригиналу переходной функции i(t). В нашем случае для нахождения оригиналов будем пользоваться теоремой разложения.
1. Составление эквивалентной операторной схемы. При переходе от исходной схемы к эквивалентной операторной схеме в общем случае необходимо ввести в ветви с конденсатором и катушкой источники ЭДС вида –Uc(0)/p и L*IL(0), учитывающие ненулевые начальные условия. Положительные направления этих ЭДС следует принять совпадающими с положительным направлением тока в данной ветви. Так как в нашем случае начальные условия нулевые, то дополнительные ЭДС не нужны. Индуктивность L учитывается на схеме замещения операторным сопротивлением pL, а емкость - 1/pC, действующая ЭДС Е источника Е(р) = Е/р.
2. Найдем операторные изображения токов во всех ветвях схемы:
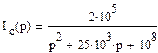
3. Найдем оригиналы полученных изображений токов с помощью теоремы разложения.
Для этого представим изображение в виде рациональной дроби:
Если степень многочлена знаменателя больше степени числителя, и уравнение H(p)=0 не имеет кратных корней, а также корней, равных корням уравнения G(p)=0, то для искомого оригинала можно записать:
где 
- производная знаменателя, pk – корни уравнения H(p)=0
Находим оригинал тока IL (p):
Аналогично:
4. Найдем напряжения на конденсаторе и на катушке индуктивности:
Вывод:
При замыкании ключа ток через конденсатор довольно резко возрастает и, достигнув определенного максимума, по мере заряда конденсатора, плавно снижается до нуля. Начальный скачек тока заряда конденсатора ограничивает присутствие в цепи последовательно включенной индуктивности, ток через которую плавно возрастает от нуля до установившегося значения. Напряжение на конденсаторе по мере его заряда плавно возрастает от нуля до половины напряжения источника питания. В момент замыкания ключа напряжение на индуктивности равняется напряжению источника питания и по мере нарастания тока уменьшается до нуля. Нарастание тока через сопротивление R1 в начальный момент времени не столь заметно, так как он шунтируется разряженным конденсатором. По мере заряда конденсатора скорость нарастания тока через R1 возрастает, и он приближается к своему установившемуся значению.
Расчет переходных процессов в цепи при синусоидальном источнике напряжения
Рассчитаем частоту, период и начальную фазу источника e(t)=Esin(ωt+ψ):
e(t)=200sin(78540t+1.8π)
1. Составление характеристического уравнения. Так как вид свободной составляющей не зависит от источника питания, то характеристическое уравнение будет таким же как и при действии источника постоянного напряжения.
Приравняв Z(p) к нулю, находим корни полученного уравнения:
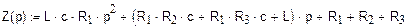
Корни действительные, свободная составляющая запишется в виде:
- Переходные функции ищем в виде:
3. Расчет принужденных значений токов и напряжений в установившемся после коммутации режиме. Расчет будем вести символическим методом в комплексных амплитудах:
Перейдем к функциям времени:
4. Определение начальных условий. Ток в катушке и напряжение на конденсаторе до коммутации, согласно основным законам коммутации скачком изменится не могут т.е
iL(-0)= iL(+0)
uc(-0)= uc(+0)
Учитывая это и то, что в начальный момент ключ был разомкнут, получим:
Расчет uL(+0) и ic (+0) произведем на основе законов Кирхгофа в схеме после коммутации для момента времени t=+0
5. Определение постоянных интегрирования. Подставим начальные условия и принужденные составляющие в уравнения пункта 2 при t=0:
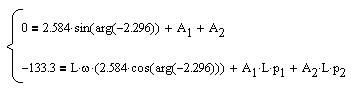
6. Представление искомых переходных функций.
Отыскав постоянные интегрирования, и определив вид свободной составляющей, запишем результат и построим графики, зависимостей iL (t), uL(t), ic(t), uc(t) и i1(t).
Вывод:
Так как вид свободных составляющих не зависит от вида воздействия, то характер графиков токов и напряжений при действии в цепи источника напряжения синусоидальной формы отличается от характера графиков при действии постоянного напряжения только видом принужденных составляющих. Как видно из графиков, напряжение на индуктивности опережает ток на 90°, а на емкости отстает на 90°, что согласуется с теорией.