2.5.1. Качественные показатели прочности. Применение конструкционных материалов постоянно сопряжено с разра-боткой инструментария, как для предварительных технико-экономических расчётов, так и для окончательной оценки полученных результатов.
Соответственно, все качественные характеристики мате-риалов должны быть представленными числовыми показа-телями и параметрами. Например, в практике машинострое-ния широко представлены понятия, отражающие свойства обрабатываемых материалов. Основными из этих свойств являются следующие свойства.
1) Прочность, то есть свойство материала сопротивлять-ся разрушению под действием внешней деформирующей си-лы.
2) Хрупкость – свойство материала разрушаться без за-метной пластической деформации.
3) Вязкость – свойство материала поглощать в заметных количествах, не разрушаясь, механическую энергию в необ-ратимой форме.
4) Твердость – свойство материала сопротивляться про-никновению в него другого тела, не получающего остаточных деформаций.
5) Ползучесть – свойство материала медленно и непре-рывно пластически деформироваться («ползти») при посто-янном напряжении.
6) Текучесть – свойство некоторых материалов за преде-лами упругости пластически деформироваться при постоян-ном или незначительно меняющемся напряжении.
7) Выносливость – свойство материала выдерживать, не разрушаясь, повторно-переменные напряжения.
8) Усталость – постепенное разрушение материала при большом числе повторно-переменных напряжений.
В указанном перечне прочность является основным ре-шающим свойством материала, и по сравнению с другими свойствами в лабораторных условиях её исследуют в первую очередь.
Хрупкость, вязкость и текучесть характеризуют работо-способность материала при динамических нагрузках.
Сведения о выносливости и усталостные характеристи-ки необходимы для оценок поведения материалов при по-вторно-переменных нагрузках.
Сведения о твердости и ползучести материала могут по-надобиться лишь в специальных случаях.
Любое свойство материала является качественной сопос-тавительной характеристикой, а для инженерной практики требуются конкретные исчисляемые параметры.
2.5.2. Количественные показатели прочности. В основе перехода от качественных характеристик к количественным (исчисляемым) показателям, всегда лежит предварительное формирование условий, предпосылок и нормирующих еди-ниц, достаточных для сравнения и отсчёта.
В случае внешнего силового воздействия на конструкци-онный материал необходимо заранее знать степень его спо-собности противостоять этому воздействию. Противостояние материала сопровождается появлением в нём деформации и напряжений. Под напряжением понимают сопротивление материала деформированию. Условно напряжение представ-ляют в виде проявляющихся в материале рассредоточенных элементарных сил, суммарный вектор которых равен вектору внешней деформирующей силы. Соответственно, средством для перехода от качественных характеристик прочности к количественным её показателям является создание мате-матической модели, способной установить связь между
внешним силовым воздействием и сопротивлением материала этому воздействию.
Процесс создания математической модели физического процесса всегда имеет ряд этапов:
а) предварительное формирование исходных условий и предпосылок;
б) аналитический анализ;
в) выбор нормирующих единиц измерения, достаточных для сравнений и расчета;
г) логико-вероятностное составление конструктивной схемы испытательного стенда для экспериментальных прове-рок;
д) создание испытательного стенда;
е) проведение экспериментального исследования и обра-ботка результатов исследования;
ж) последующая экспериментальная проверка степени пригодности сформированной математической модели для инженерных расчётов.
В соответствии с перечнем указанных этапов в своё время было установлено, что для получения численных показате-лей механической прочности конструкционных материалов надо вести испытания на растяжение (сжатие) образцов, изго-товленных из испытываемых материалов, прикладывая изме-ряемую, а потому – известную возрастающую величину де-формирующей силы и доводя образец до разрушения. В этих условиях под воздействием внешней деформирующей силы в материале возникают исчисляемые значения деформации и напряжения.
2.5.2.1. Деформация – изменение формы или размеров те- а (или его части), обусловленное изменением относительно-го положения частиц тела в результате их перемещения. Из-меняются межатомные расстояния и перегруппировываются блоки молекул и зерен.
В общем случае материал деформируется под действием механических сил, электрического и магнитного полей, из-за изменения температуры, усадки материала.
Деформация называется упругой, если она исчезает после удаления вызвавшей ее нагрузки, и пластической, если она после снятия нагрузки не исчезает.
Как упругую, так и пластическую деформацию можно свести, в конечном счете, к двум наиболее простым видам:
1) растяжение (или сжатие), то есть деформация, при которой удлиняется (или укорачивается) тело вдоль какой-либо оси;
2) сдвиг, то есть деформация, при которой искажаются углы между осями (направлениями перемещений).
Для тел, имеющих форму бруса, в теории сопротивления материалов различают 4 основных вида деформации: растя-жение (или сжатие); сдвиг; изгиб; кручение.
Численные значения деформации находят в результате измерений конкретных геометрических параметров испыты-ваемых образцов, подвергаемых испытаниям, назначаемых для определения механических свойств материалов. При этом различают:
а) абсолютную деформацию, представляющую собой ве-личину, например, фактического удлинения (или укорочения)
 исследуемого размера l0;
исследуемого размера l0;
б) относительную деформацию  в виде отношения
в виде отношения
 ; (1.1)
; (1.1)
в) истинную относительную деформацию  , исчисляе-мую в каждый текущий момент времени по уравнению
, исчисляе-мую в каждый текущий момент времени по уравнению
 , (1.2)
, (1.2)
где дифференциал dl представляет собой бесконечно малую величину абсолютной деформации, возникающей в каждый момент времени деформирования.
Конечную величину  находят интегрированием уравне-ния (1.2) в пределах изменения размера l, а именно: в диапа-зоне от конечной (увеличившейся) длины lK до начальной длины l0:
находят интегрированием уравне-ния (1.2) в пределах изменения размера l, а именно: в диапа-зоне от конечной (увеличившейся) длины lK до начальной длины l0:
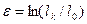 . (1.3)
. (1.3)
Связь между относительной  и истинной относительной
и истинной относительной  деформациями имеет вид
деформациями имеет вид
 . (1.4)
. (1.4)
Из уравнения (1.4) следует, что численный результат рас-чета по уравнениям (1.1) и (1.3) практически одинаков толь-ко в случаях, когда  . Кроме того, удобство использо-вания истинной относительной степени деформации
. Кроме того, удобство использо-вания истинной относительной степени деформации  в кри-вых упрочнения заключается в том, что она обладает свойст-вом аддитивности (это свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин его частей при любой разбив-ке объекта на части). В свою очередь, истинные относитель-ные деформации, выраженные через изменения линейных размеров, при растяжении и сжатии являются эквивалентны-ми по упрочняющему эффекту.
в кри-вых упрочнения заключается в том, что она обладает свойст-вом аддитивности (это свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин его частей при любой разбив-ке объекта на части). В свою очередь, истинные относитель-ные деформации, выраженные через изменения линейных размеров, при растяжении и сжатии являются эквивалентны-ми по упрочняющему эффекту.
2.5.2.2. Напряжение, возникающее в материале, условно представляют в виде некоторого силового поля, рассредото-ченного в деформируемом материале. Это силовое поле соз-даёт противодействие внешней деформирующей силе. Сило-вое поле охватывает каждую единицу площади поперечного (или продольного) сечения деформируемого материала. При этом имеется в виду, что упоминаемое сечение расположено
перпендикулярно (или продольно) к направлению внешней деформирующей силы Р, измеряемой в процессе испытаний.
Для расчётов принимают условие, что в каждый момент времени интегральная сила, предопределяемая напряжениями материала, равна величине внешней деформирующей силы. То есть руководствуются третьим законом Ньютона о ра-венстве действия и противодействия между двумя телами.
Возникающая в деформируемом материале пластическая деформация в реальности распределена по объему материала неравномерно. Соответственно, неравномерно распределяет-ся и напряжение. Математически корректно учесть эту не-равномерность не представляется возможным. Поэтому при составлении модели деформирования условно считают, что любой бесконечно малый в виде кубика объем материала, взятый в очаге деформации, при произвольной ориентации относительно координатных осей имеет на своих гранях нор-мальные (перпендикулярные к граням) напряжения  и каса-тельные (лежащие в плоскости граней) напряжения
и каса-тельные (лежащие в плоскости граней) напряжения 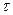 .
.
Когда направления нормальных напряжений  совпадают с направлением внешней деформирующей силы, нормальные напряжения получают свое максимальное значение и счита-ются главными, а касательные напряжения исчезают. То есть складываются условия для разрушения материала (отрыв). И наоборот, когда касательные напряжения совпадают с на-правлением деформирующей силы, они считаются главными, а исчезают нормальные напряжения
совпадают с направлением внешней деформирующей силы, нормальные напряжения получают свое максимальное значение и счита-ются главными, а касательные напряжения исчезают. То есть складываются условия для разрушения материала (отрыв). И наоборот, когда касательные напряжения совпадают с на-правлением деформирующей силы, они считаются главными, а исчезают нормальные напряжения  . Здесь создаются усло-вия для чистого сдвига в толще материала.
. Здесь создаются усло-вия для чистого сдвига в толще материала.
При формировании технологических процессов часто ма-тематический анализ поведения материала обрабатываемого тела ведут, пользуясь прямоугольной системой координат X, Y, Z. При этом в общем случае считают, что в материале де-формируемого тела всегда возникают, например, нормальные напряжения, действующие вдоль каждой из осей координат.
Но все тела по соотношениям своих геометрических размеров подразделяются на три группы:
1)объёмные тела со значительными габаритными разме-рами относительно каждой из координатных осей;
2) плоские тела типа листов и полос;
3) осесимметричные тела типа прутков малых поперечных сечений.
Соответственно считают, что для первой группы тел ха-рактерной является объёмная схема напряжений; для второй группы схема напряжений плоская, так как утонением листов чаще всего можно пренебречь; для третьей группы – осевая (линейная), если уменьшением диаметра в процессе дефор-мирования можно пренебречь:
Стандартные испытания материалов на прочность (по ме-тоду растяжения) ориентированы на линейную схему напря-жений в материале испытываемого образца. То есть при ис-пытаниях полагают, что направление главного нормального напряжения  совпадает с направлением внешней деформи-рующей силы.
совпадает с направлением внешней деформи-рующей силы.
Этими испытаниями устанавливают следующие характе-ристики, которые дают возможность получить количествен-ную оценку ранее перечисленным основным свойствам мате-риалов.
1) Предел прочности (временное сопротивление)  – напряжение при наибольшем силовом воздействии, предше-ствующим разрушению испытываемого образца. При этом наибольшим называют напряжение, при котором в материале растягиваемого образца начинает развиваться процесс шей-кообразования (в этот момент начинается переход от одноос-ного наряженного состояния к объемному напряженному со-стоянию).
– напряжение при наибольшем силовом воздействии, предше-ствующим разрушению испытываемого образца. При этом наибольшим называют напряжение, при котором в материале растягиваемого образца начинает развиваться процесс шей-кообразования (в этот момент начинается переход от одноос-ного наряженного состояния к объемному напряженному со-стоянию).
2) Предел упругости  – напряжение, при котором ос-таточные деформации впервые достигают некоторой малой
– напряжение, при котором ос-таточные деформации впервые достигают некоторой малой
величины, устанавливаемой техническими условиями на ма-териал (обычно при удлинении образца на 0,002 % от l0).
3). Предел текучести 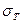 . Для ряда металлов и сплавов существует понятие о физическом пределе текучести, опреде-ляемом как наименьшее напряжение, при котором, несмотря на продолжающуюся пластическую деформацию испытывае-мого образца, не происходит заметное увеличение деформи-рующей силы. Но для очень большого числа металлов поня-тие о физическом пределе текучести отсутствует. Для та-ких металлов введено понятие о техническом (условном) пределе текучести, определяемом величиной напряжения, при котором остаточная деформация образца достигает неко-торой величины, устанавливаемой техническими условиями. Наиболее распространенным в технике условием является выбор напряжения, соответствующего увеличению базовой длины образца l0 на 0,2 %.
. Для ряда металлов и сплавов существует понятие о физическом пределе текучести, опреде-ляемом как наименьшее напряжение, при котором, несмотря на продолжающуюся пластическую деформацию испытывае-мого образца, не происходит заметное увеличение деформи-рующей силы. Но для очень большого числа металлов поня-тие о физическом пределе текучести отсутствует. Для та-ких металлов введено понятие о техническом (условном) пределе текучести, определяемом величиной напряжения, при котором остаточная деформация образца достигает неко-торой величины, устанавливаемой техническими условиями. Наиболее распространенным в технике условием является выбор напряжения, соответствующего увеличению базовой длины образца l0 на 0,2 %.
4) Предел ползучести – напряжение, при котором де-формация через определенные промежутки времени от нача-ла ползучести получает весьма малые значения, определяе-мые техническими условиями.
Анализ смыслового содержания всех упомянутых форму-лировок о численных величинах основополагающих напря-жениях показывает, что все эти величины условны, так как все они сформированы с учётом вполне конкретных исход-ных условий.
При этом следует иметь в виду, что началом отсчёта во всех известных системах измерения являются условные вели-чины и понятия (метр, секунда, ангстрем, вольт, ампер и т.д.).
2.5.2.3. Связь между напряжениями  и
и 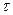 . Между нор-мальными и касательными напряжениями установлена мате-матическая связь [6,7]. Эта связь положена в основу сформи-рованного условия пластичности (гипотеза Сен-Венана – Треска). Суть гипотезы в следующем: под действием внеш-
. Между нор-мальными и касательными напряжениями установлена мате-матическая связь [6,7]. Эта связь положена в основу сформи-рованного условия пластичности (гипотеза Сен-Венана – Треска). Суть гипотезы в следующем: под действием внеш-
ней деформирующей силы материал начинает переходить в пластическое состояние, когда одно из главных касательных напряжений получает максимальное значение, равное поло-вине предела текучести, найденного при испытаниях на рас-тяжение. То есть
 . (1.5)
. (1.5)
По мере роста степени деформации в процессе испытаний образцов на растяжение начинает нарушаться условие о ли-нейной (одноосной) схеме напряженного состояния.
Для того, чтобы учитывать конкретную схему напряжен-ного состояния, зависимость (1.5) скорректирована, а имен-но: по условию Мизеса – Губера в эту зависимость введен ко-эффициент Лодэ  учитывающий возможное наличие как плоской, так и объемной схем напряженного состояния:
учитывающий возможное наличие как плоской, так и объемной схем напряженного состояния:
 . (1.6)
. (1.6)
Коэффициент  находится в диапазоне
находится в диапазоне
 . (1.7)
. (1.7)
В результате при линейной схеме напряженного состоя-ния, когда ещё не наблюдается существенного утонения базо-вого участка растягиваемого образца,  = 1,0; а при объём-ной схеме, когда на утоняющемся базовом участке образца появляется утонение в виде шейки, –
= 1,0; а при объём-ной схеме, когда на утоняющемся базовом участке образца появляется утонение в виде шейки, –  = 1,15.
= 1,15.
Так как наиболее реальным считается существование объ-емной схемы напряженного состояния материала, то с учетом зависимостей (1.6) и (1.7) зависимость (1.5) получает вид
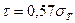 . (1.8)
. (1.8)
2.5.2.4. Связь между прочностью и твердостью. Твер-дость материала определяют по результатам вдавливания в его поверхность специального инструментального тела в виде шарика заданного диаметра или пирамиды, рабочим элемен-том которой является её вершина.
В процессе вдавливания измеряют величину деформи-рующей силы прибора (твердомера), которую затем сопос-тавляют с характерными последеформационными геометри-ческими параметрами очага деформации. Результатом сопос-тавления является конкретное число с размерностью напря-жения. В зависимости от шкалы твердомера, получаемые чис-ленные значения твердости сопровождают наименованием шкалы (твердость по Бринеллю, Роквеллу, Шору и др.).
Так как природа прочности и твердости материалов едина, то экспериментально установлены соотношения между этими величинами. Эти соотношения являются справочными дан-ными. Например, при сопоставлении ряда характеристик уг-леродистых сталей обычно принимаемой за эталон сталь Ст. 45. У этой стали предел прочности  = 650 МПа при твер-дости НВ
= 650 МПа при твер-дости НВ  179. Соответственно
179. Соответственно 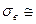 3,6 НВ.
3,6 НВ.
2.5.2.5. Диаграмма «напряжение – деформация». Числен-ные показатели механической прочности конструкционных материалов определяют преимущественно на основе испыта-ния лабораторных образцов материала на растяжение.
Конструктивно испытываемый образец чаще всего пред-ставляет собой цилиндрическое тело с утолщёнными закон-цовками, предназначенными для прикладывания к образцу внешней деформирующей силы. Срединная рабочая часть об-разца диаметром до 10 мм в соответствии со стандартом обычно имеет длину 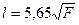 . Здесь F – площадь попереч-ного сечения образца. Отклонение по диаметру базовой ра-бочей части образца не должно превышать ±0,1 мм.
. Здесь F – площадь попереч-ного сечения образца. Отклонение по диаметру базовой ра-бочей части образца не должно превышать ±0,1 мм.
Чтобы в процессе деформирования исключить влияние инерционных сил на величину сопротивления материала, скорость приложения внешней деформирующей силы огра-ничивают до (2 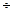 10) мм/мин.
10) мм/мин.
При испытаниях принимают условие, что образец в про-цессе растяжения находится в одноосном напряженном со-стоянии вплоть до момента, когда по мере удлинения начи-нается шейкообразование на испытываемом образце.
Автоматически записываемая графическая зависимость между деформирующей силой Р и абсолютной деформацией  образца представляет собой кривую растяжения. Эта кри-вая является характеристикой прочности испытываемого об-разца из конкретного материала. Для того, чтобы перейти от показателей прочности конкретного образца к показателям прочности самого материала, кривую растяжения перестраи-вают в координаты относительных напряжений (
образца представляет собой кривую растяжения. Эта кри-вая является характеристикой прочности испытываемого об-разца из конкретного материала. Для того, чтобы перейти от показателей прочности конкретного образца к показателям прочности самого материала, кривую растяжения перестраи-вают в координаты относительных напряжений ( ) и относительных деформаций (
) и относительных деформаций ( ). Здесь F0 – пло-щадь начального поперечного сечения образца. 10 — начальная длина базовой части испытываемого образца.
). Здесь F0 – пло-щадь начального поперечного сечения образца. 10 — начальная длина базовой части испытываемого образца.
Перестроенная таким образом кривая получила название кривая упрочнения материала, исследуемого на механическую прочность.
Так как на практике часто при силовом воздействии на ма-териал имеет место очень большой объем пластической де-формации, то для корректности последующих расчётов кри-вую упрочнения перестраивают в координаты «условное на-пряжение - истинная относительная деформация», то есть
«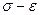 ».
».
2.5.2.6. Сущность упрочнения. Действие внешней дефор-мирующей силы приводит в движение мельчайшие частицы во всём объёме деформируемого объекта, приводя их к скольжению в нескольких плоскостях. Как правило, скольже-ние сопровождается двойникованием, то есть образованием
закономерных сростков кристаллов. В этих сростках какая-либо важная грань одного кристалла, называемая двойнико-вой плоскостью, накладывается на такую же грань другого кристалла.
Двойникование происходит при статическом деформиро-вании и сравнительно чаще – при деформировании ударом. Оно сопутствует деформации скольжения и в ряде случаев способно влиять на величину силы, необходимой для дефор-мирования.
Есть специальная теория дислокаций, то есть перемещения в плоскости скольжения отдельных несовершенств простран– ственной кристаллической решетки. Предметами вниманий этой теории являются краевые и винтовые дислокации, пере-ползание дислокаций, их возникновение и размножение, ско-рость движения и взаимодействие и т.д.
Под действием скольжения и двойникования возникаю-щие в материале напряжения несколько возрастают. Эффект этого роста получил название упрочнение материала, кото-рое основывается на нарушении естественного взаимного расположения атомов в кристаллической решетке материала, на изменении межатомных расстояний, увеличении плотно-сти дислокаций.
Энергия, затрачиваемая на деформирование, частично ак-кумулируется в кристалле в виде потенциальной энергии и частично выделяется в виде тепла. Таким образом, вблизи плоскости скольжения, то есть вблизи пачки атомных слоев, принимающих участие в сдвиге при скольжении или двойни-ковании, атомы отклоняются от положения своего устойчиво-го равновесия и по окончании деформирования остаются в напряжённом, неустойчивом положении. Соответственно, с позиций дислокационной теории пластическая деформация представляет собой эстафетное перемещение дислокаций (несовершенств кристаллической решётки) в плоскости скольжения. Накопление дислокаций на различных направле-
ниях приводит к усилению их взаимодействия и сопровожда-ется упрочнением монокристалла (наклёпом).
2.5.2.7. Математическая модель испытаний на проч-ность. Кривая упрочнения материала является основным, экспериментально получаемым источником сведений о проч-ности конструкционного материала. Наиболее важные пока-затели прочности в табличном виде представлены в справоч-ной литературе, где указаны пределы прочности, текучести, упругости и другие параметры. То есть в справочниках пред-ставлены главнейшие (отправные) точки кривых упрочнения. В то же время в производственных условиях часто требуется иметь полную кривую упрочнения. Это объясняется уровнем жесткости требований, предъявляемым к служебной работо-способности изготавливаемых деталей. Так, исходя из эксплу-атационных требований к деталям, все заготовки для изго-тавливаемых деталей разделены на четыре группы контроля.
Соответственно, все заготовки, входящие в 1-ю группу контроля, должны иметь дополнительную массу с объёмом и конфигурацией, достаточными для изготовления стандартных образцов к испытаниям материала на прочность. Предпри-ятие-потребитель самостоятельно вырезает из дополнитель-ной массы образцы и экспериментально получает кривую уп-рочнения для своих нужд, связанных с технико-эконо-мической оценкой изготовляемой продукции.
Заготовки, входящие во 2-ю группу контроля, поставля-ются малыми партиями (обычно 5 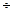 10 штук). Одна из заго-товок этой партии имеет дополнительную массу для изготов-ления образцов к испытаниям на прочность, а проверке на твердость подвергается вся партия заготовок, так как показа-тель твёрдости является достаточным для идентификации прочности материала всех заготовок данной партии.
10 штук). Одна из заго-товок этой партии имеет дополнительную массу для изготов-ления образцов к испытаниям на прочность, а проверке на твердость подвергается вся партия заготовок, так как показа-тель твёрдости является достаточным для идентификации прочности материала всех заготовок данной партии.
Заготовки 3-ей группы контроля подвергаются только про-верке на твердость, а для идентификации прочности исполь-
зуют справочные сведения о показателях прочности (в пер-вую очередь имеются в виду предел прочности и предел те-кучести).
Заготовки 4-й группы контроля проверяют только по нали-чию клейма и другим вспомогательным сопроводительным документам, подтверждающим марку материала.
Таким образом, у заготовок 3-ей и 4-й группы контроля нет экспериментально полученных кривых упрочнения. Со-ответственно, нет сведений о величине напряжений, которые могут возникать в обрабатываемом материале заготовок в основном диапазоне деформаций (от предела текучести до предела прочности), но могут быть необходимыми для проек-тирования технологических процессов обработки.
Это отсутствие объясняется тем, что эксплуатационные требования к деталям, изготовляемым из заготовок 3-ей и 4-й групп контроля, допускают возможность пользоваться не-полными усредненными справочными данными. Например, даны только численные значения основных прочностных по-казателей. В этом случае отсутствие в справочниках сведений о соотношении напряжений и соответствующих им деформа-ций в диапазоне между пределом текучести и пределом прочности компенсируют тем, что формируют посредством аппроксимации математическую модель кривой упрочнения.
Термин «аппроксимация» происходит от латинского «ap-proximo», что означает – «приближаю».
В рассматриваемом случае сущность аппроксимации в том, что экспериментально получаемую кривую упрочнения заме-няют такой теоретической кривой, которая имеет своё кон-кретное математическое описание и имеет форму графика очень близкую форме типовой экспериментальной кривой.
Очень близкой по форме к экспериментальной кривой уп-рочнения является кривая степенной зависимости типа
у = Вхn. (1.9)
Цель аппроксимации – установить прямую функциональ-ную математическую связь между напряжением и деформа-цией.
Применительно к имеющимся обозначениям переменных параметров кривой упрочнения зависимость (1.9) принимает вид
 (1.10)
(1.10)
где величины В и n являются коэффициентами аппрокси-мации.
Коэффициенты аппроксимации представляется возмож-ным вычислять на основании предварительного условия: две точки на экспериментальной и теоретической кривой являют-ся общими. Такими точками берут имеющиеся в справочни-ках точку А с координатами предела текучести [ 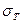 ;
;  ] и точ-ку Б – с координатами предела прочности [
] и точ-ку Б – с координатами предела прочности [ 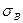 ;
;  ].
].
Указанные координаты являются местом расположения предела текучести (точка А) и предела прочности (точка Б) на кривой упрочнения.
Наличие координат двух точек даёт возможность на осно-ве уравнения (1.10) получить систему, состоящую из двух уравнений с двумя неизвестными:
 ;
;
 .
.
В соответствии с этим коэффициенты вычисляют по сле-дующим уравнениям:
 ;(1.11)
;(1.11)
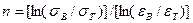 . (1.12)
. (1.12)
Тогда, вычислив для конкретного случая коэффициенты В и п, а также, располагая значением истинной относитель-ной деформации  , находят по уравнению (1.10) напряже-ния
, находят по уравнению (1.10) напряже-ния  , возникающие в обрабатываемом материале под дейст-вием внешней деформирующей силы.
, возникающие в обрабатываемом материале под дейст-вием внешней деформирующей силы.
2.5.2.8. Напряжения, обусловленные высокоскоростным ударом. В ряде случаев конструкционный материал в процес-се обработки, а также эксплуатируемые изготовленные дета-ли подвергаются высокоскоростному удару. В машинострое-нии к такой категории удара относят случаи, при которых си-ловое взаимодействие инструмента с обрабатываемым мате-риалом начинается при скоростях 5 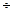 100 м/с.
100 м/с.
Практика показывает, что под действием высокоскорост-ного удара материал (металлы и сплавы) ведут себя иначе, чем при медленном (статическом) силовом взаимодействии. Возникающие в материале напряжения, противодействующие удару, резко изменяются: возрастают или падают. Это предо-пределяется физическими свойствами материала и ростом инерционных сил, сопутствующих как быстро перемещаю-щемуся инструменту, так и покоящемуся деформируемому материалу.
Так как величина напряжений является показателем проч-ностных свойств деформируемого материала, то естествен-ным стремлением была попытка выявить закономерности роста напряжений и установить числовые значения этих на-пряжений в зависимости от степени деформации, аналогично обычным испытаниям материалов по методу испытаний на растяжение. Однако результаты отечественных и зарубежных исследований [8] показали неприемлемость метода высоко-скоростных испытаний на растяжение. Основным доводом явилась невозможность идентифицировать возникающей в процессе удара величину деформирующей (разрушающей) силы, так как предварительное статическое взвешивание си-
лы в процессе тарировки измерительной системы не учитыва-ет инерционных сил., сопутствующих удару.
В то же время рациональный выбор исходных условий и предпосылок даёт возможность установить математическую зависимость между возникающим напряжением и степенью пластической деформации. При этом интенсивность удара следует оценивать удельной энергией, то есть количеством энергии, приходящимся на единицу пластически деформи-руемого объёма [9,10] в процессе свободной осадки испыты-ваемого образца.
Исходные предпосылки и условия. 1). Накопленный прак-тикой машиностроения опыт проверки и испытаний конст-рукционных материалов на их работоспособность [10] пока-зывает, что для установления математической зависимости между напряжением и деформациями, возникающими под действием высокоскоростного удара, наиболее предпочти-тельным является процесс свободной осадки цилиндрических образцов со стандартными размерами диаметра d0 и высоты h0. В этом случае представляется возможным:
а) принимать величину истинной относительной дефор-мации  в каждый момент деформирования как отношение бесконечно малой абсолютной деформации dh, к текущему значению высоты h:
в каждый момент деформирования как отношение бесконечно малой абсолютной деформации dh, к текущему значению высоты h:
 ,
,
ав течение всего процесса деформирования брать интеграль-ное значение истинной относительной деформации:
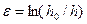 ;
;
б) легко доступным способом измерять скорость 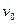 под-лёта инструмента к деформируемому образцу [11]. Это даёт возможность при известной наносящей удар массе М вычис-лять величину номинальной энергии удара Е = 0,5 М
под-лёта инструмента к деформируемому образцу [11]. Это даёт возможность при известной наносящей удар массе М вычис-лять величину номинальной энергии удара Е = 0,5 М  и переходить к нормирующей единице в виде удельной энергии (то есть приходящейся на каждую единицу деформируемого объёма) еуд=Е/V, где V – объём испытываемого цилиндри-
и переходить к нормирующей единице в виде удельной энергии (то есть приходящейся на каждую единицу деформируемого объёма) еуд=Е/V, где V – объём испытываемого цилиндри-
ческого образца. Значимость понятия «удельная энергия» со-стоит в следующем:
– с одной стороны, эта относительная величина способна предопределить минимально необходимое количество вво-димой энергии, достаточной для выявления предельной воз-можности деформируемого материала сопротивляться де-формирующей силе удара;
– с другой стороны – удельная энергия физически связана с сопротивлением материала, которое предопределяется ве-личиной напряжения  , представляющим собой элементар-ный вектор и являющимся структурным элементом возни-кающего в материале силового поля, суммарный вектор кото-рого эквивалентен внешней деформирующей силе Р удара.
, представляющим собой элементар-ный вектор и являющимся структурным элементом возни-кающего в материале силового поля, суммарный вектор кото-рого эквивалентен внешней деформирующей силе Р удара.
2) Весь объём упругих деформаций отнесен к элементам конструкции, которые передают силу удара, обрабатываемому объекту.
3) Весь объем пластических деформаций сосредоточен в материале деформируемого образца. Соответственно, образец рассматривается как идеальное жесткопластичное тело, имеющее напряжение  , постоянное для каждой скорости
, постоянное для каждой скорости 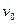 удара.
удара.
4) Масса пластически деформируемого образца достаточ-но мала, и этой массой при аналитическом анализе можно пренебречь.
5) Образец подвергается двухстороннему удару верхней массы m1 и нижней массы m2. Движение масс кинематиче-ски связано, и приведенная масса составляет:
М=т1 т2/(т1+ т2). (1-13)
6) Векторы скоростей 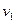 и
и  масс т1 и т2 совпадают с прямой, соединяющей центры тяжести этих масс, то есть реа-лизуется центральный удар.
масс т1 и т2 совпадают с прямой, соединяющей центры тяжести этих масс, то есть реа-лизуется центральный удар.
Уравнения движения рассматриваемых масс в соответст-вии со вторым законом Ньютона имеют вид:
 ; (1.14)
; (1.14)
 , (1.15)
, (1.15)
где 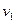 и
и  – скорость первой и второй массы, соответственно.
– скорость первой и второй массы, соответственно.
Так как  ;
; 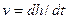 ;
;  , где
, где  – мгновен-ная скорость, t – время, Р – сила удара,
– мгновен-ная скорость, t – время, Р – сила удара,  – напряжение в материале, f – текущая площадь поперечного сечения образ-ца, то при этом совместное решение уравнений движения приводит к уравнению деформирования:
– напряжение в материале, f – текущая площадь поперечного сечения образ-ца, то при этом совместное решение уравнений движения приводит к уравнению деформирования:
 . (1.16)
. (1.16)
Интегрирование полученного уравнения даёт закон гаше-ния скорости удара в процессе пластического деформирова-ния:
 . (1.17)
. (1.17)
Найденное решение справедливо для холодного деформи-рования таких материалов, как чистое железо, медь, свинец, сталь с малым содержанием углерода, алюминиевые сплавы В96, АК6, некоторые титановые и другие сплавы. У перечис-ленных металлов и сплавов при динамическом нагружении широкому диапазону изменения степени деформации соот-ветствует неизменная для каждой скорости удара величина сопротивления деформации (то есть возникающего в мате-риале напряжения). Это и даёт основание считать, что высо-коскоростным ударом деформируемый материал можно рас-сматривать как идеальное жестко пластичное тело.
К концу движения инструмента, когда  = 0, из уравнения
= 0, из уравнения
(1.17) следует:
 , (1.18)
, (1.18)
где  — максимальная степень деформации, получаемая в конце удара:
— максимальная степень деформации, получаемая в конце удара:
 . (1.19)
. (1.19)
Здесь hк – конечная высота образца после удара.
В результате, зная массу М, наносящую удар, скорость 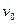 удара, геометрические размеры обрабатываемого образца и конечную величину степени деформации
удара, геометрические размеры обрабатываемого образца и конечную величину степени деформации  , представляется возможным определять максимальную силу Р удара, возни-кающей в конце процесса:
, представляется возможным определять максимальную силу Р удара, возни-кающей в конце процесса:
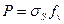 , (1-20)
, (1-20)
где f v, – площадь поперечного сечения осаженного образца.
Величина Р необходима для проектирования работоспо-собной системы силопередающих элементов, которые по ис-ходному условию должны работать исключительно в диапа-зоне упругой деформации.