Системы случайных величин

На практике часто бывает так, что результаты опыта описываются не одной, а несколькими случайными величинами Например, если опыт - работа предприятия за некоторый период времени, то он может характеризоваться такими величинами:

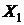- количество работающих;

- величина произведенной продукции;

- фонд заработной платы;

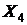- количество поставщиков;

- количество потребителей и т.д.

Результаты такого опыта, как медосмотр, также могут быть описаны несколькими случайными величинами: 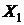- возраст, - рост, - вес, 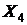- наличие хронических заболеваний и т.д. В таких случаях говорят, что речь идет о системе случайных величин (), которую еще называют многомерной случайной величиной или случайным вектором. Величины называются компонентами системы или координатами многомерной случайной величины (случайного вектора). В систему могут входить только дискретные случайные величины, или только непрерывные, или и те, и другие. Свойства системы определяются не только свойствами отдельных входящих в систему величин, но и взаимодействием, связью между ними. Например, число работающих на предприятии и величина произведенной продукции обычно связаны между собой, также как часто бывают связаны возраст и наличие хронических заболеваний. Это обстоятельство учитывается при описании и исследовании многомерных случайных величин.

Как и в одномерном случае, случайный вектор полностью описывается своим распределением, т.е. указанием всех возможных значений с соответствующими вероятностями. Распределение системы двух ДСВ и 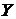можно представить в виде таблицы:

			...
			...
			...
...	...	...	...	...	...
			...
			...

В первой строке таблицы указаны все значения, которые принимает компонента : 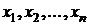, в первом столбце - значения, которые принимает компонента 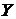: 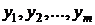. В клетках указаны вероятности . Для вычисления числовых характеристик отдельных величин и составления условных распределений удобно в последнем столбце и последней строке таблицы указать вероятности и , равные сумме вероятностей по строкам и столбцам соответственно. Должно выполняться условие:

.

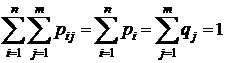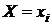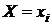Если зафиксировать значение одной из компонент, например взять , то можно вычислить условную вероятность при условии, что . Набор значений с соответствующими условными вероятностями называют условным распределением при 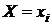. Аналогично можно получить условное распределение при , т.е. соответствие между значениями Х и условными вероятностями .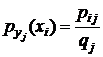

Полное описание распределения системы двух и более случайных величин весьма громоздко, поэтому при исследовании системы стараются ограничиться ее числовыми характеристиками. В первую очередь, это числовые характеристики отдельных компонент системы:

Взаимосвязь между величинами отражает коэффициент ковариации

,

равный математическому ожиданию произведения отклонений компонент и 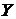от своих математических ожиданий.

Если выписать формулу для вычисления в системе двух ДСВ, то станет наглядным его смысл:

.

Если для каждой пары значений отклонения наблюдаются в одну и ту же сторону от математического ожидания, то все произведения вида будут одного знака и в данном случае будет больше (по модулю), чем для систем, где эти произведения разного знака. Из формулы для также видно, что его абсолютная величина зависит не только от совместного поведения и 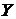, но и от величины разброса значений и относительно и 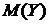. Чтобы исключить влияние этого обстоятельства, вводят безразмерный коэффициент корреляции:

.

Учитывая, что 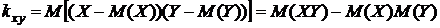для коэффициента корреляции получим выражение:

.

Значения коэффициента корреляции заключены в следующих пределах:

.

Если , то говорят о положительной корреляции, если , то говорят об отрицательной корреляции.

Для независимых случайных величин коэффициент корреляции , однако обратное утверждение неверно, т.е. равенство не является доказательством независимости величин.

Крайние значения коэффициента корреляции свидетельствуют о наличии функциональной зависимости между и .

Отличие коэффициента корреляции от 0 говорит о наличии связи между величинами, т.е. об их коррелированности.

При изучении математики, других естественных наук обычно рассматривают функциональную зависимость между двумя величинами, суть которой заключается в том, что какая-либо величина определяется как однозначная функция одной или нескольких других величин.

Между случайными величинами может существовать и связь другого рода, проявляющаяся в том, что одна из них реагирует на изменение другой изменением своего закона распределения. Связь такого рода называется статистической (стохастической).

Она наблюдается между двумя случайными величинами обычно тогда, когда имеются общие факторы, влияющие как на одну, так и на другую величину наряду с другими, неодинаковыми для данных величин факторами. Так, если , а , то величины и статистически связаны. Наиболее явно такая зависимость проявляется в изменении числовых характеристик условного распределения одной величины при изменении значений другой.

Зависимость условного математического ожидания от значений Х называется регрессией по . Аналогично, зависимость условного математического ожидания называется регрессией по .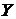

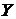Предположим теперь, что зависимость от значений описывается линейной функцией (линейная регрессия): . Будем выбирать и так же, как в методе наименьших квадратов. Решая эту задачу подобно тому, как это делалось ранее при исследовании функций нескольких переменных, получим уравнение линейной регрессии по :

.

Аналогично можно получить и уравнение линейной регрессии по :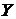

.