Задание 4 Транспортная задача с ограничениями на пропускную способность

Пусть требуется при решении транспортной задачи ограничить перевозки от поставщика с номером l к потребителю с номером k.

Возможны ограничения двух типов:

1. x_lk ≥ a. Прежде чем решать задачу необходимо сократить запасы l -го поставщика и запросы k -го потребителя на величину a. В полученном оптимальном решении следует увеличить объем перевозки x_lk на величину a.

2. x_lk ≤ b. Прежде чем решать задачу необходимо вместо k -го потребителя с запросами b_k ввести двух других потребителей. Один из них с номером k должен иметь запросы 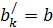, а другой с номером n+1 – запросы b_n+1=b_k – b. Стоимости перевозок для этих потребителей остаются прежними, за исключением стоимости c_l(n+1), которая принимается равной сколь угодно большому числу М. после получения оптимально решения величины грузов, перевозимых к n+1- му потребителю, прибавляются к величинам перевозок k -го потребителя. Так как c_l(n+1) = М – самая большая стоимость перевозки, то в оптимальном решении клетка с номером (l, n+1) останется пустой и объем перевозки x_lk не превзойдет b.

Пример 4

Решить транспортную задачу, исходные данные которой приведены в таблице, при дополнительных условиях: объем перевозки груза от второго поставщика второму потребителю должен быть не менее 200 единиц (х₂₂ ≥ 200), а от третьего первому – не более 300 единиц (х₃₁ ≤ 300).

bj ai
	2	9	10
	2	11	13
	4	10	12

Для того чтобы в оптимальном решении объем перевозки х₂₂ был не менее 200 единиц, при решении задачи будем предполагать, что запасы второго поставщика а₂ и запросы второго потребителя b₂ меньше фактических на 200 единиц. После получения оптимального решения объем перевозки х₂₂ увеличим на 200 единиц.

Для того чтобы удовлетворить требованию х₃₁ ≤ 300, вместо первого потребителя введем двух других. Один из них под прежним первым номером имеет запросы b₁ = 300 единиц и прежние стоимости перевозок единиц груза. Другому присвоим четвертый номер. Его запросы равны b₄ = 600 – 300 = 300 единиц и стоимости перевозок единиц груза те же, что и у первого потребителя, за исключением с₃₄, которую примем равной сколь угодно большому числу М, т.е. с₃₄ = М. После нахождения оптимального решения задачи объемы перевозок для четвертого потребителя необходимо прибавить к соответствующим объемам перевозок для первого потребителя.

В результате указанных преобразований таблица исходных данных задачи будет иметь следующий вид:

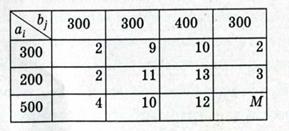
Далее задачу решаем обычным методом потенциалов. Проверяем выполнение необходимого и достаточного условия существования решения задачи. Находим суммарные запасы поставщиков и запросы потребителей:

а₁ + а₂ + а₃ = 300 + 200 + 500 = 1000;

b₁ + b₂ + b₃ + b₄ = 1300.

Задача с неправильным балансом. Вводим фиктивного поставщика с запасами а₄ =1300 – 1000 = 300 единиц.

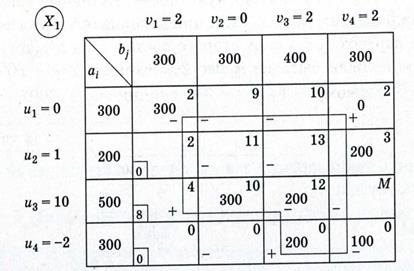
Составляем начальное опорное решение Х₁ методом минимальной стоимости и находим потенциалы. Вычисляем оценки для свободных клеток таблицы. Все оценки положительные, кроме оценки 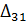= 8. Находим цикл для клетки (3, 1). Он состоит из клеток (3, 1), (1, 1), (1, 4), (4, 4), (4, 3), (3, 3). Находим величину груза для перераспределения по означенному циклу = 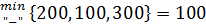при (i, j) = (4. 4). Осуществляем сдвиг по этому циклу на величину = 100, получаем второе опорное решение Х₂.

Решение Х₂ оптимальное, так как все оценки неположительные. Запишем оптимальное решение исходной задачи. Для этого увеличим объем перевозки х₂₂ на 200 единиц и объединим объемы перевозок четвертого потребителя с объемами перевозок первого потребителя. Получим

Вычислим значение целевой функции на оптимальном решении:

Z(X^*) = 2 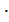300 + 2 200 + 11 200 + 4 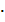100 + 10 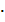300 + 12 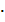100 = 7800.

Ответ: min Z(X) = 7800 при 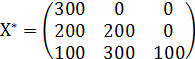.