ОУ ВО ЮЖНО-УРАЛЬСКИЙ ИНСТИТУТ УПРАВЛЕНИЯ И ЭКОНОМИКИ
КАРТОЧКА РЕЦЕНЗЕНТА
Домашняя контрольная работа
По дисциплине _____________________________________________________________________
Студента _____________________________________________________________________
(Фамилия, имя, отчество)
Группа __________Специальность _____________________________________
Дата проверки «__» _________________________________200__г.
Оценка _________________________________________________
Преподаватель ________________________________________ ______________
(Фамилия, имя, отчество) (подпись)
РЕЦЕНЗИЯ
СОДЕРЖАНИЕ
| Методические рекомендации по выполнению контрольных заданий… Рекомендации по выполнению контрольной работы | |
| Задания для домашней контрольной работы…………………………… | |
| Рекомендуемый список литературы…………………………………….. |
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ
Краткий перечень основных понятий теории графов
Теория графов как теоретическая дисциплина может рассматриваться как раздел дискретной математики, исследующий свойства конечных множеств (бесконечные графы не будут вводиться в рассмотрение) с заданными отношениями между их элементами. Как прикладная дисциплина теория графов позволяет описывать и исследовать многие физические, технические, экономические, биологические, социальные и другие системы. Например, графом, изображенным на рис. 1, в котором точки − вершины графа − города, линии, соединяющие вершины − ребра − дороги, соединяющие города, описывается так называемая транспортная задача (задача нахождения кратчайшего пути из одного города- пункта в другой).
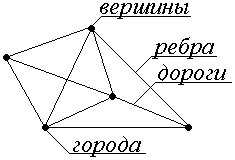
Рис. 1.
Формальное определение графа таково. Пусть задано конечное множество V, состоящее из n элементов, называемых вершинами графа, и подмножество X декартова произведения V×V, то есть 
, называемое множеством дуг, тогда ориентированным графом D называется совокупность (V, X). Неориентированным графом G называется совокупность множества V и множества ребер − неупорядоченных пар элементов, каждый из которых принадлежит множеству V.
Одинаковые пары - параллельные или кратные ребра;
Кратностью ребер называют количество одинаковых пар.
Рис.2.
Например, кратность ребра { v 1,v2} в графе, изображенном на рис. 2, равна двум, кратность ребра { v 3,v4} − трем.
Граф называется ориентированным, если пары (v, w) являются упорядоченными.
Ребра ориентированного графа называются дугами.
Итак, используемые далее обозначения:
V – множество вершин;
X – множество ребер или дуг;
v (или vi)– вершина или номер вершины;
G, G 0 - неориентированный граф;
D, D 0 – ориентированный;
{ v, w } − ребра неориентированного графа;
{ v, v } – обозначение петли;
(v, w) − дуги в ориентированном графе;
v, w - вершины, x, y, z – дуги и ребра;
n (G), n (D) количество вершин графа;
m (G) - количество ребер, m (D) - количество дуг.
Примеры
1) Ориентированный граф D =(V, X), V ={ v 1, v 2, v 3, v 4},
X ={ x 1=(v 1, v 2), x 2=(v 1, v 2), x 3=(v 2, v 2), x 4=(v 2, v 3)}.
Рис. 3.
2) Неориентированный граф G =(V, X), V ={ v 1, v 2, v 3, v 4, v 5},
X ={ x 1={ v 1, v 2}, x 2={ v 2, v 3}, x 3={ v 2, v 4}, x 4={ v 3, v 4}}.
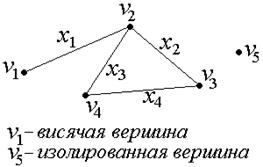
Рис. 4.
Понятия смежности, инцидентности, степени
Если x ={ v, w } - ребро, то v и w − концы ребра x.
Если x =(v, w) - дуга ориентированного графа, то v − начало, w – конец дуги.
Вершина v и ребро x неориентированного графа (дуга x ориентированного графа) называются инцидентными, если v является концом ребра x (началом или концом дуги x).
Вершины v, w называются смежными, если { v, w }Î X.
Вершина графа, имеющая степень 0 называется изолированной, а степень 1 – висячей.
Маршруты и пути
Последовательность v 1 x 1 v 2 x 2 v 3... x k v k+1, (где k ³1, v iÎ V, i =1,..., k +1, x iÎ X, j =1,..., k), в которой чередуются вершины и ребра (дуги) и для каждого j =1,..., k ребро (дуга) x j имеет вид { vj, vj +1} (для ориентированного графа (vj, vj +1)), называется маршрутом, соединяющим вершины v 1 и vk +1 (путем из v 1 в vk +1).
Пример
В графе, изображенном на рис.4, v 1 x 1 v 2 x 2 v 3 x 4 v 4 x 3 v 2 - маршрут, v 2 x 2 v 3 x 4 v 4 – подмаршрут; маршрут можно восстановить и по такой записи x 1 x 2 x 4 x 3;
Цепь − незамкнутый маршрут (путь), в котором все ребра (дуги) попарно различны.
Цикл − замкнутая цепь (в неориентированном графе).
Контур − замкнутый путь (в ориентированном графе).
Простой путь (цепь) − путь (цепь, цикл, контур), в котором ни одна дуга/ребро не встречается дважды.
Простой цикл (контур) − цикл (контур), в котором все вершины попарно различны.
Гамильтонова цепь (путь, цикл, контур) − простая цепь (путь, цикл, контур), проходящая через все вершины.
Эйлерова цепь (путь, цикл, контур) − цепь (путь, цикл, контур), содержащая все ребра (дуги) графа по одному разу.
Длина маршрута (пути) − число ребер в маршруте (дуг в пути).
Утверждение 1. Для того чтобы связный псевдограф G обладал Эйлеровым циклом, необходимо и достаточно, чтобы степени всех его вершин были четными.
Утверждение 2. Для того чтобы связный псевдограф G обладал Эйлеровой цепью, необходимо и достаточно, чтобы он имел ровно 2 вершины нечетной степени.