(в соответствии с Методическими рекомендациями по проведению школьного и муниципального этапов Всероссийской олимпиады школьников в 2018/2019 учебном году по математике, утверждёнными на заседании Центральной предметно-методической комиссии Всероссийской олимпиады школьников по математике, протокол № 2 от 13.06.2018 г.)
Абсолютно верное решение (в том числе, не совпадающее с каноническим) – 7 баллов.
Верное решение, имеющее небольшие недочеты, в целом не влияющие на решение – 6-7 баллов.
Решение, содержащее незначительные ошибки, пробелы в обоснованиях, но в целом верно которое могло бы стать полностью
правильным после небольших исправлений или дополнений – 5-6 баллов.
Верно рассмотрен один из двух (более сложный) существенных случаев – 4 балла.
Доказаны вспомогательные утверждения, помогающие в решении задачи – 2-3 балла.
Рассмотрены отдельные важные случаи при отсутствии решения (или при ошибочном решении) – 1балл.
Решение отсутствует или неверное, продвижения отсутствуют – 0 баллов.
а) любое правильное решение оценивается в 7 баллов. Недопустимо снятие баллов за то, что решение слишком длинное, или за то, что решение школьника отличается от приведенного в методических разработках или от других решений, известных жюри; при проверке работы важно вникнуть в логику рассуждений участника, оценивается степень ее правильности и полноты;
б) олимпиадная работа не является контрольной работой участника, поэтому любые исправления в работе, в том числе зачёркивание ранее написанного текста, не являются основанием для снятия баллов; недопустимо снятие баллов в работе за неаккуратность записи решений при ее выполнении;
в) баллы не выставляются «за старание», в том числе за запись в работе большого по объёму текста, не содержащего продвижений в решении задачи;
г) победителями олимпиады в одной параллели могут стать несколько участников, набравшие наибольшее количество баллов, поэтому не следует в обязательном порядке «разводить по местам» лучших участников олимпиады.
Выполнение заданий не предполагает использование каких-либо справочных материалов, средств связи и электронно-вычислительной техники.
Участникам во время проведения олимпиады запрещено иметь при себе любые электронные вычислительные устройства или средства связи (в том числе и в выключенном виде), учебники, справочные пособия.
РЕШЕНИЯ ЗАДАЧ
Класс
1. Возможны три варианта: либо фразу „Я девочка” сказал Витя, либо Лена, либо Саша. В 1-ом случае (Витя назвал себя девочкой), т. е. сказал неправду, значит, Лена и Саша сказали правду. Но они сказали, что они – мальчики. Получили противоречие. Значит, этот вариант не удовлетворяет условию. Во 2-ом случае (девочкой назвала себя Лена) выходит, что Лена сказала правду. Вторую правду сказал Витя (он – мальчик, вне всякого сомнения), следовательно, ложь была произнесена Сашей, т. е. Сашина фраза „Я мальчик” ложна, и Саша – это девочка. Наконец, в 3-ем случае (Саша назвалО себя девочкой), получается, что Лена и Витя назвались мальчиками. При этом фраза Лены – ложь, следовательно, все остальные, а, значит, и Саша сказали правду. Таким образом, Саша – девочка.
Итак, 1-го случая быть не может, а во всех других получается, что Саша – девочка, и её полное имя – Александра.
2. Это сделать можно. Например, так, как показано на рис. справа. (Существуют и другие способы.)
3. Их всего пять: 22 + 23, 14 + 15 + 16, 7 + 8 + 9 + 10 + 11, 5 + 6 + 7 + 8 + 9 + 10.
4. Можно. Например, разрезать квадрат на 4 равных квадрата, затем 2 из них разрезать каждый на 4 равных квадрата.
5. 2018 = 2·1009, а числа 2 и 1009 – простые. Поэтому, кроме написанного произведения возможны ещё только такие: 2018 = 1·2·1009, 2018 = 1·1·2·1009, 2018 = 1·1·1·2·1009. Соответственно, суммы равны 1011, 1012, 1013,1014.
Класс
1. Существует. Например, 132.
2. См. задачу № 2 для 5 класса.
3. См. задачу № 3 для 5 класса.
4. Можно. Например, так, как показано на рис. справа.
5. 2018 = 2·1009, а числа 2 и 1009 – простые. Поэтому, кроме написанного произведения возможны ещё только такие: 2018 = 1·2·109, 2018 = 1·1·2·1009, 2018 = 1·1·1·2·1009, 2018 = 1·1·1·1·2·1009. Соответственно, суммы равны 1011, 1012, 1013, 1014, 1015.
- 4 -
Класс
1. Не существуют. Выражение, стоящее в левой части, принимает всегда чётное значение, а в правой – нечётное.
2. См. задачу № 2 для 5 класса.
3.
4. Можно. Например, так, как показано на рис. справа.
5. 2018 = 2·1009, а числа 2 и 1009 – простые. Поэтому, кроме написанного произведения возможны ещё только такие: 2018 = 1·2·1009, 2018 = 1·1·2·1009, 2018 = 1·1·1·2·1009, 2018 = 1·1·1·1·2·1009., 2018 = 1·1·1·1·1·2·1009. Соответственно, суммы равны 1011, 1012, 1013, 1014, 1015, 1016.
Класс
1. См. задачу № 1 для 7 класса.
2. Обозначим через D середину стороны AC, а через E – точку пересечения биссектрисы и медианы. Поскольку CE – высота и биссектриса в треугольнике BCD, то BC = 0,5 AC и, следовательно, BC < AC. Осталось рассмотреть три ситуации.
1) a – „средняя” сторона, тогда a = 1, b = 2, c = 0. Ясно, что такой случай невозможен.
2) b – „средняя” сторона, тогда b = 2, a = 1, c = 3. Такой случай тоже невозможен, т. к. нарушается неравенство треугольника. 3) c – „средняя” сторона, тогда b = c + 1, a = c – 1. Но нам известно, что b = 2 a. Тогда: c + 1 = 2 (c – 1), откуда c = 3, b = 4, a = 2. Это и есть единственный ответ на задачу.
3. См. задачу № 3 для 7 класса.
4. x 2 – y 2 + 7 x + 12= (x 2 + 7 x + 12) – y 2 = (x + 3,5)2 – y 2 = (x + 3,5 – y) (x + 3,5 + y).
5. 2018 = 2·1009, а числа 2 и 1009 – простые. Поэтому, кроме написанного произведения возможны ещё только такие: 2018 = 1·2·1009, 2018 = 1·1·2·1009, 2018 = 1·1·1·2·1009, 2018 = 1·1·1·1·2·1009, 2018 = 1·1·1·1·1·2·1009, 2018 = 1·1·1·1·1·1·2·1009. Соответственно, суммы равны 1011, 1012, 1013, 1014, 1015, 1016, 1017.
Класс
1. Если x = y = 0, то все четыре числа нули, и положительных чисел среди них нет. Если x = y = 1, то положительным является только 2 x + y. Если x =2, y = 1, то положительных чисел будет два. Если x = 3, y = 1, то три положительных числа. Все четыре числа положительными быть не могут. Доказательство метолом от противного. Предположим, что 2 x + y > 0, x – y > 0, x – 2 y > 0, y – 2 x > 0, но тогда и сумма этих чисел 2 x – y положительна. Но ведь это – (y – 2 x), т. е. число отрицательное. Противоречие. Итак, ответ: 0, 1, 2 или 3.
2. См. задачу № 2 для 8 класса.
3. См. задачу № 4 для 8 класса.
4. См. задачу № 1 для 7 класса.
5. 2018 = 2·1009, а числа 2 и 1009 – простые. Поэтому, кроме написанного произведения возможны ещё только такие: 2018 = 1·2·1009, 2018 = 1·1·2·1009, 2018 = 1·1·1·2·1009, 2018 = 1·1·1·1·2·1009, 2018 = 1·1·1·1·1·2·1009, 2018 = 1·1·1·1·1·1·2·1009,
2018 =1·1·1·1·1·1·1·2·1009. Соответственно, суммы равны 1011, 1012, 1013, 1014, 1015, 1016, 1017, 1018.
Класс
1. Пусть студент сдал на первом курсе x экзаменов, тогда на втором экзаменов не меньше x + 1, на третьем – не меньше x + 2, на четвёртом – не меньше x + 3. Следовательно, общее число экзаменов, сданных студентом за 5 лет, не меньше 7 x + 6, откуда: 31 ≥ 7 x + 6 Û x £ 25/7 (1).
С другой стороны, поскольку студент сдал на пятом курсе 3 x экзаменов, то на четвёртом курсе экзаменов не больше 3 x – 1, на третьем – не больше 3 x – 2, на втором – не больше 3 x – 3. Значит, общее число экзаменов за 5 лет не больше 13 x – 6, а потому: 31 £ 13 x – 6 Û x ³ 37/13 (2).
Одновременно неравенствам (1) и (2) удовлетворяет только одно целое число – это 3. Значит, на первом курсе 3 экзамена, на пятом – 9. Поскольку мы ранее установили, что на четвёртом курсе экзаменов не меньше x + 3 и не больше 3 x – 1, то искомое число экзаменов на четвёртом курсе не меньше 6 и не больше 8.
Если бы на четвёртом курсе было 6 экзаменов, то всего студент сдал бы не больше, чем 3+4+5+6+9 = 27 экзаменов, что противоречит условию.
А если бы на четвёртом курсе было 7 экзаменов, то всего студент сдал бы не больше, чем 3+5+6+7+9 = 30 экзаменов, и это тоже противоречит условию.
Остался вариант, когда на четвёртом курсе 8 экзаменов. Но его нельзя автоматически объявлять ответом на задачу. Надо показать, что этот вариант реализуется. Действительно, если количество экзаменов на курсах, например, таково: на 1-ом – 3, на 2-ом – 4, на 3-ем – 7, на 4-ом – 8, на 5-ом – 9, то всё соответствует условию. Ответ: 8 экзаменов.
2. См. задачу № 2 для 9 класса.
- 5 -
\
3. Сделаем замену:Тогда данное уравнение запишется так:
После простых преобразований уравнение сводится к квадратному u 2 – 4 u + 4 = 0, в левой части которого – точный квадрат, так что у него единственный корень u = 2. Возвращаясь к прежним переменным, имеем:
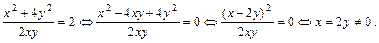
Следовательно, стоящая в условии задача поиска минимального значения выражения (x – 3)2 + 2 xy эквивалентна задаче отыскания минимального значения (x – 3)2 + x 2. Последнее выражение есть 2 x 2 – 6x + 9 – квадратный трёхчлен, и наименьшее значение он принимает при x = 1,5. Само же минимальное значение равно 4,5.
4. См. задачу № 1 для 9 класса.
5. 2018 = 2·1009, а числа 2 и 1009 – простые. Поэтому, кроме написанного произведения возможны ещё только такие: 2018 = 1·2·1009, 2018 = 1·1·2·1009, 2018 = 1·1·1·2·1009, 2018 = 1·1·1·1·2·1009, 2018 = 1·1·1·1·1·2·1009, 2018 = 1·1·1·1·1·1·2·1009, 2018 = 1·1·1·1·1·1·1·2·1009, 2018 = 1·1·1·1·1·1·1·1·2·1009. Соответственно, суммы равны 1011, 1012, 1013, 1014, 1015, 1016, 1017, 1018, 1019..
Класс
1. Задача сводится к нахождениювсех тех a, при которых условиям x 2 + x + a = 0 (1) и 2 x – a ¹ 0 (2) одновременно удовлетворяет единственный x. А это значит, что необходимо найти те a, при которых уравнение (1) имеет ровно один корень, удовлетворяющий условию (2). Это, очевидно, возможно только в двух случаях:
1) уравнение (1) имеет один корень, и он удовлетворяет (2);
2) уравнение (1) имеет два различных корня, и один из них не удовлетворяет (2).
Рассмотрим каждую ситуацию.
1) Дискриминант (1) должен быть нулевым, т.е. a = 1/4. Тогда корнем является число –1/2, которое, очевидно, удовлетворяет условию (2).
2) Дискриминант (1) положителен, т. е. a < 1/4. Так как один из корней не удовлетворяет условию (2), то он равен a /2. Подставляя это значение в уравнение (1), получим: a 2 + 6 a = 0 Û a = 0 или a = – 6.
Итак, ответ: a = 1/4, a = 0, a = – 6.
2. Можно. Точки располагаются, например, в вершинах октаэдра (см. первый из рис. справа). Его боковыми гранями являются правильные треугольники ABC, ACD, ADE, AEB, FBC, FCD, FDE, FEB, и потому все расстояния, кроме BD, EC, AF, очевидно, равные. Ясно и то, что BD = EC. Равенство EC = AF. также, очевидно, верно. Поэтому условие задачи выполнено.
Есть и другой способ: расположить шесть точек в вершинах правильной пятиугольной пирамиды (см. второй из рис. справа).
3. Докажем, что, начиная с 3-го, все члены последовательности равны sin(–80)0, т.е. при любом n ³ 3 имеет место равенство: sin(10 n)0 = sin(–800), или, что то же самое, sin(10 n)0 = sin(10000) (1).
Поскольку наименьший положительный период синуса равен 3600, то справедливость равенства (1) будет следовать из того, что 10 n – 1000 кратно 360 при любом натуральном n ³ 3. Докажем это. 10 n – 1000 = = 1000 (10 n – 3 – 1). Первый множитель (1000) делится на 40, а второй (10 n – 3 – 1) при n = 3 равен нулю, а при n > 3 есть не что иное как число из n – 3 девяток, т.е. в любом случае кратен 9. Значит, их произведение кратно 360, что и требовалось доказать.
Следовательно, все члены последовательности, начиная с четвёртого, отрицательны. Первые же три члена положительны. Значит, ответ на задачу: 3.
 |
4. Используем традиционные обозначения: a, b – катеты, c – гипотенуза треугольника, S – его площадь, j – величина острого угла, h – длина высоты, опущенной на гипотенузу, p – полупериметр, r – радиус вписанной окружности. Тогда:
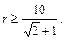
Так как значение любого синуса не больше 1, то Докажем, что круг радиуса r имеет площадь больше, чем 50, т. е.
p r 2 > 50 Û r 2 > 50/p (*). Для этого докажем неравенство
Неравенство (**) очевидно, если заметить, что 3 + 2< 3 + 3 = 6 < 2p. Значит, верно и более слабое неравенство (*).
5. 2018 = 2·1009, а числа 2 и 1009 – простые. Поэтому, кроме написанного произведения возможны ещё только такие: 2018 = 1·2·1009, 2018 = 1·1·2·1009, 2018 = 1·1·1·2·1009, 2018 = 1·1·1·1·2·1009, 2018 = 1·1·1·1·1·2·1009, 2018 = 1·1·1·1·1·1·2·1009, 2018 = 1·1·1·1·1·1·1·2·1009, 2018 = 1·1·1·1·1·1·1·1·2·1009, 2018 = 1·1·1·1·1·1·1·1·1·2·1009 Соответственно, суммы равны 1011, 1012, 1013, 1014, 1015, 1016, 1017, 1018, 1019, 1020, 1021.