Таблица степеней «хороших»чисел
| 22=4 | 23=8 | 24=26 | 25=32 | 26=64 | 27=128 | 28=256 | 29=512 | 210=1024 |
| 32=9 | 33=27 | 34=81 | 35=243 | 36=729 | ||||
| 52=25 | 53=125 | 54=625 | ||||||
| 62=36 | 63=216 | |||||||
| 72=49 | 73=343 |
Свойства степеней
1. При умножении показатели складываются:  (основания одинаковые) (основания одинаковые)
| 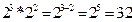
| ||
2. При делении показатели вычитаются:  (основания одинаковые) (основания одинаковые)
| 
| ||
3. При возведении степени в степень показатели перемножаются: 
| 
| ||
4. Если показатели одинаковые, то основания можно перемножать или делить:  и и  Следствие: все можно вносить под один корень:
Следствие: все можно вносить под один корень:
 ; ; 
| 

 
| ||
5. Любое число в нулевой стпени равно 1: 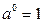
| 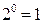
| ||
6. Если показатель отрицательный, то основание
«переворачивается», а у показателя убирается «минус»: 
| 

| ||
7. При извлечении корня показатели делятся:  (это свойство часто используется «справа налево»)
Следствие: любой корень можно представить как дробную степень:
(это свойство часто используется «справа налево»)
Следствие: любой корень можно представить как дробную степень: 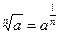
|  или
или

| ||
Полезные советы:
1) Десятичные дроби лучше представлять в виде простых – и в основаниях, и в показателях:
Пример: 
2) При преобразованиях корни удобнее представлять как дробные степени; а когда надо будет вычислить значение, надо опять дробные степени представить в виде корня:
Пример: 
3) Если есть степени с разными основаниями, то можно одно из оснований представить как произведение других:
Пример: 
Внимание!
Если в степень возводится скобка, то надо возводить в эту степень ВСЕ множители, которые стоят в скобке! (не забыть возвести в степень числа! и потом привести подобные!)
Пример:
 (в знаменателе тройка возвелась в квадрат!)
(в знаменателе тройка возвелась в квадрат!)
2. Показательные уравнения – где х стоит в показателе степени, например 
| Как решать | Пример 1: 
| Пример 2: 
|
| 1) Все степени приводим к одному основанию (в качестве основания берем «хорошее число») |  ( ( ) )
| 
|
| 2) Пользуясь свойствами степеней, упрощаем | Здесь упрощать нечего | 
|
| 3) Убираем основания | 
| 
|
| 4) Решаем получившиеся уравнения | 
| 
|
| 5) Пишем ответ | Ответ: х=0 | Ответ: х=1 |
| Если к одному основанию не привести | Пример 1: 
| Пример 2: 
|
| 1) Приводим все степени к одному показателю | Здесь и так показатели одинаковые | 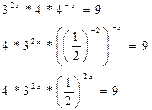
|
| 2) Если степени с разных сторон от знака равенства, делим на любую из них; если с одной стороны – перемножием | 
| 
|
| 3) Дальше должно привестись к одному основанию, и основания можно убрать | 
| 
|
| 4) Решаем получившееся уравнение | 
| 
|
| 5) Пишем ответ | Ответ: х=-2 | Ответ: х=1 |
Простейшие показательные неравенства
Показательные неравенства решаются точно так же, как показательные уравнения.
Но! Если основание меньше единицы, то, когда мы убираем основания, знак неравенства меняется.
Например:
 Здесь мы убрали показатели, сохранив знак неравенства «<»
Здесь мы убрали показатели, сохранив знак неравенства «<»
|  Здесь, убрав показатели, мы поменяли знак неравенства с «<» на «>»
Здесь, убрав показатели, мы поменяли знак неравенства с «<» на «>»
|  Поэтому, чтобы не путаться, лучше всегда переходить к целому основанию
Поэтому, чтобы не путаться, лучше всегда переходить к целому основанию
|
4. Логарифм числа а по основанию b - это показатель степени, в которую надо возвести b, чтобы получить a.
То есть если  , то
, то  Значит, чтобы найти логарифм, надо решить показательное уравнение.
Значит, чтобы найти логарифм, надо решить показательное уравнение.
Пример: Найти  : Пусть
: Пусть  =х, решаем уравнение:
=х, решаем уравнение:  . Значит,
. Значит,  =2,5
=2,5
Логарифмы можно брать только от положительных чисел!
Основание лоарифма должно быть положительным и не равно 1!
Логарифм единицы равен нулю!
Десятичный логарифм – логарифм по основанию 10. Записывается 
Натуральный логирифм – логарифм по основанию e. Записывается 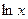 (е – иррациональное число, ≈2,718)
(е – иррациональное число, ≈2,718)
5. Основное логарифмическое тождество:  (Пример:
(Пример:  )
)
Полезные советы:
1) не забываем про свойства степеней! Пример: Найти  =
=  =
= 
2) если число, возводимое в степень, не такое, как основание логарифма, то надо это число представить в виде степени, и потом использовать свойства степеней: Пример: 
3) в более сложных случаях показатель степени преобразуется по свойствам логарифмов (см. дальше)
Пример: 
Любое число можно представить как логарифм, например, 
Свойства логарифмов
1. Если числа перемножаются, то их логарифмы складываются:

| 
| |
2. Если числа делятся, то их логарифмы вычитаются: 
| 
| |
Следствие: 
| 
| |
3. Показатель степени выносится за логарифм  (часто это свойство применяется «справа налево»)
(часто это свойство применяется «справа налево»)
| 

| |
4. Формула перехода к новому основанию: 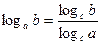 (эта формула часто используется «справа налево»)
(эта формула часто используется «справа налево»)
| 
|
Следствие 1:  (часто используется, когда логарифмы умножаются,
и если делятся логарифмы одного и того же числа, тогда по этому свойству:
(часто используется, когда логарифмы умножаются,
и если делятся логарифмы одного и того же числа, тогда по этому свойству:
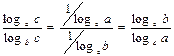
| 

|
Следствие 2:  = = 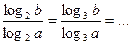 (то есть все равно, какое брать основание)
(то есть все равно, какое брать основание)
| 
|
Следствие 3:  (степень основания выносится за логарифм в знаменатель)
(степень основания выносится за логарифм в знаменатель)
| 
|
5.  (низ и верх можно менять местами) (низ и верх можно менять местами)
| 
|
Некоторые примеры задач
| 1) Если подряд записаны два логарифма (или несколько), то они вычисляются справа налево: | 
|
Такие примеры нельзя путать с теми, где логарифмы просто перемножаются: 
| |
| 2) Если логарифм возводится в квадрат (или другую степень), показатель степени пишется прямо над логарифмом: | 
|
| 3) В заданиях, где есть сумма или разность логарифмов: Если перед логарифмами стоят числа, то надо сначала эти числа «перетащить в показатели степени» Если слагаемых несколько, то слагаемые с «плюсом» пишем в числителе дроби, а с «минусом» - в знаменателе Все десятичные дроби представляем в виде простых! Внимательно следим, чтобы основания логарифмов были одинаковыми! Если основания разные, то переходим к одному основанию, при этом какой-то логарифм должен легко вычисляться. | 


|
| 4) Если логарифмы стоят в показателе степени, то применяем свойства степеней и основное логарифмическое тождество: | 
|
| 5) При умножении и делении неберущихся логарифмов надо переходить к новому основанию: | |
| Иногда: сразу по формуле перехода (справа налево) Если логарифмы перемножаются, то один из них можно перевернуть и получить нужную дробь: Если берутся логарифмы от одного числа, но по разным основаниям, удобно перевернуть оба логарифма: Отдельно стоящие числа (слагаемые) представляются в виде логарифмов: | 


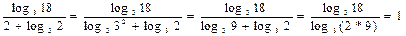
|
| 7. Простейшие логарифмические уравнения | 
| 
|
| 1) Отдельностоящие числа представляем как логарифмы | 

|  
|
| 2) Переносим слагаемые из одной части в другую, чтобы не было знаков «минус» | 
| |
3) Используем свойство 
| 
| |
4) Используем свойство 
| 
| |
| 5) Убираем логарифмы | 
| 
|
| 6) Решаем получившееся уравнение | 
| 
|
| 7) ОБЯЗАТЕЛЬНО подставляем получившиеся корни в ИСХОДНОЕ уравнение и убеждаемся, что под логарифмами получаются положительные числа |  - верно! - верно!
| 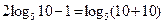 верно! верно!
 -нет! -нет!
|
| 8) Пишем ответ: | Ответ: х=6 | Ответ: х=10 |
Логарифмические уравнения, где х стоит в основании логарифма, решаются как обычные. Но корни проверяются на выполнение следующих условий: основание логарифма должно быть больше 0 и не равно 1.
Пример:  Решение:
Решение:  ;
; 
Проверяем корни: 
 И ответ в этом уравнении x=12
И ответ в этом уравнении x=12
Логарифмические уравнения, где логарифм стоит в показателе степени, решаются по основному логарифмическому тождеству. Для этого, возможно, придется перейти к новому основанию. Пример: 
Решение: 
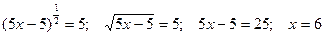
Проверяем корень: 
| 8. Простейшие логарифмические неравенства | 
|
| 1) Выполняем преобразования так же, как при решении логарифмических уравнений, до того момента, когда надо будет убрать логарифмы (или один из них) |  
|
| 2) Убираем логарифмы, и заменяем одно неравенство системой. Первое неравенство системы – то, которое получится, если из исходного неравенства убрать логарифмы Второе (и остальные) неравенства системы получаются из ОДЗ: То, то чего берется логарифм, должно быть больше 0 Внимание! Если основание логарифма меньше 1, то, когда убираем логарифмы, знак неравенства меняем! |
 Внимание! Поменяли знак неравенства, потому что основание логарифма было меньше 1!
Внимание! Поменяли знак неравенства, потому что основание логарифма было меньше 1!
|
| 3) Решаем получившуюся систему | 
|
| 4) Пишем ответ: | Ответ: 
|
| Тест 1 степени и логарифмы | Тест 2 степени и логарифмы | |||
Вычислить  при х=3 при х=3
| Вычислить  при х=5 при х=5
| |||
Вычислить  при а=4 при а=4
| Вычислить  при а=64 при а=64
| |||
Вычислить  + + 
| Вычислить 
| |||
Вычислить 
| Вычислить 
| |||
Вычислить 
| Вычислить 
| |||
Решить уравнение 
| Решить уравнение 
| |||
Рещить уравнение 
| Рещить уравнение 
| |||
Решить уравнение 
| Решить уравнение 
| |||
Решить неравенство 
| Решить неравенство 
| |||
Решить неравенство 
| Решить неравенство 
| |||
Вычислить 
| Вычислить 
| |||
Вычислить 
| Вычислить 
| |||
Вычислить 
| Вычислить 
| |||
Вычислить 
| Вычислить 
| |||
Вычислить 
| Вычислить 
| |||
Вычислить 
| Вычислить 
| |||
Решить уравнение 
| Решить уравнение 
| |||
Решить уравнение  (меньший) (меньший)
| Решить уравнение 
| |||
Решить неравенство 
| Решить неравенство 
| |||
Решить неравенство 
| Решить неравенство 
|