Цель работы
Исследование переходных процессов в простейших линейных электрических цепях при включении их под действие источников постоянного напряжения, а также переходных процессов возникающих при замыкании этих цепей.
Краткая теория
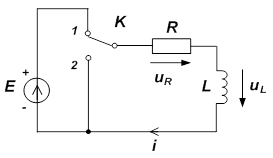
Переходный процесс, протекающий при включении R, L - цепи к источнику постоянной ЭДС Е (рис. 1) (ключ K мгновенно переключается из положения 2 в положение 1), описывается линейным, неоднородным дифференциальным уравнением первого порядка, составленным по второму закону Кирхгофа
, (1)
где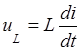 
- напряжение самоиндукции, возникающее на катушке индуктивности L при изменении тока в ней.
- напряжение на активном сопротивление R.
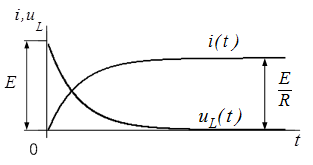
Рис. 1 Рис. 2
Решением этого дифференциального уравнения является следующая искомая функция, описывающая характер изменения тока во времени
, (1)
где 
- принужденная составляющая тока (установившееся значение тока после коммутации);
A – постоянная интегрирования;
p – корень характеристического уравнения.
Характеристическое уравнение
, откуда 
.
Полагаем, что до коммутации ток в цепи отсутствовал, т.е. при t = 0
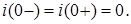
(2)
Из (1) следует, что 
, а решения для тока и напряжения на индуктивности принимают вид:
; 
. (3)
Как видно из выражения для 
в момент срабатывания ключа (t = 0) на катушке скачком возникает ЭДС, по величине равная напряжению E. Затем uL(t) постепенно уменьшается до нуля из-за уменьшения скорости нарастания тока.
Графики изменения тока и напряжения на индуктивности приведены на рис. 2.
Рассмотрим теперь, что происходит в этой цепи в дальнейшем.
При отключении катушки с током от источника E (ключ K мгновенно переключается из положения 1 в положение 2), электрическая цепь принимает вид рис. 3.
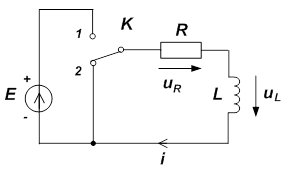
Рис. 3 Рис. 4
Переходный процесс описывается однородным дифференциальным уравнением, причем ток в момент коммутации (см. 3) на основании первого закона коммутации (ток в катушке не может измениться скачком) i(0)= 
,
, решение которого имеет вид
, (4)
, 
.
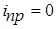Напряжение на индуктивности
. (5)
Как видно из (4) и (5) ток плавно уменьшается до нуля, а напряжение uL (t) скачком изменяет знак с (+) на (-). Это происходит потому, что ток в катушке не может измениться скачком и после отключения источника продолжает протекать в том же направлении, постепенно уменьшаясь по величине. При этом на катушке возникает напряжение обратной полярности, т.к. производная по току изменила свой знак. Графики изменения 
и приведены на рис. 4.
Скорость протекания переходного процесса характеризуется постоянной времени цепи 
.
Постоянная времени численно равна времени за которое исследуемая функция изменяется в е раз. При экспериментальном исследовании переходных процессов постоянная времени цепи определяется графическим путем. Так как свободная составляющая тока или напряжения описывается
уравнением 
, производная в любой точки этой кривой
, следовательно, для определения постоянной
времени в этом случае можно измерить длину подкасательной, соответствующей какому либо значению у (рис 5) и умножить её на масштаб времени.
Рис. 5
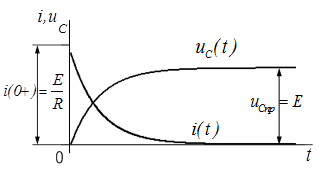
Рис. 6 Рис. 7
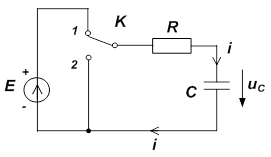
Рассмотрим процесс заряда конденсатора, т.е. каким образом будет нарастать с течением времени напряжение uC(t) (рис. 6) (ключ K мгновенно переключается из положения 2 в положение 1).
Общее решение для напряжения на емкости при решении задачи классическим методом имеет вид
. (6)
Полагаем, что до коммутации конденсатор не заряжен, т.е. при 
напряжение 
, а при 
конденсатор должен зарядиться до напряжения, равного E, после чего ток станет равным нулю. Из (6) следует, что 
, а решения для тока и напряжения принимают вид
и 
. (7)
Графики изменения напряжения и тока в RC - цепи приведены на рис. 7. Они показывают, что напряжение на емкости не устанавливается мгновенно, а плавно изменяется по экспоненциальному закону от нуля до установившейся величины, равной Е; а ток в момент коммутации возрастает скачком до величины 
и затем плавно по экспоненциальному закону уменьшается до нуля.
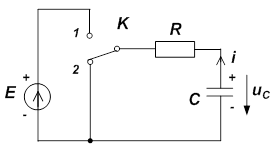
Рис. 8 Рис. 9
Если теперь мгновенно отключить источник E и мгновенно подключить к конденсатору сопротивление R, то начнется процесс разряда конденсатора. К этому моменту времени конденсатор зарядился до напряжения источника E, т.е. началом нового отсчета времени считаем uC(0+) = E. Тогда дифференциальное уравнение имеет вид
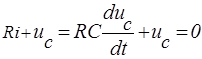(8)
Принужденная составляющая uC пр = 0 и решение уравнения 8 имеет вид uC(t) = Aept. Так как uC(0-) = uC(0+) = E, 
, 
, то
, 
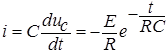(9)
Графики изменения uC (t) и i(t) приведены на рисунке 9.
Включение цепи на прямоугольный импульс
Переходные процессы в большинстве случаев являются однократными и кратковременными. Их непосредственное наблюдение с помощью обычного осциллографа является невозможным. Поэтому для исследования переходных процессов коммутацию делают многократной и периодической, что достигается питанием цепи от импульсного источника, т.е. источника периодических сигналов прямоугольной формы. Такой режим воздействия на электрическую цепь обычно получают при периодическом переключении электронного ключа К из положения 2 в положение 1, а затем наоборот из положения 1 в положение 2.(в цепи рис. 10 а, рис. 10 б).
|
|
|
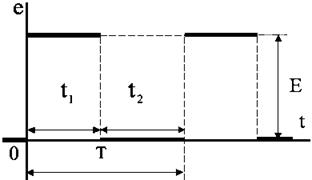
t1 - длительность импульса 
t2 - длительность паузы 
- период сигнала источника
- частота источника
Рис. 10. а, б, в.
Рис. 11 Рис. 12
Рис. 13 Рис. 14
Чтобы переходный процесс заканчивался за время подачи импульса, его длительность должна быть t1 > 5τ. Передний фронт импульса соответствует включению цепи на постоянное напряжение (ключ K переключается в положение 1), а задний - уменьшению напряжения источника до нуля (ключ K переключается в положение 2). В исследуемых схемах начальные условия должны быть нулевыми, поэтому длительность паузы должна быть t2 > 5τ. Это обстоятельство позволяет на экране осциллографа или монитора наблюдать реакцию цепи на импульсное воздействие, а также найти установившиеся значения исследуемых кривых до и после коммутации. На рис. 12 и рис. 14 показаны кривые токов и напряжений, которые будут отражать переходные процессы в R, L и R, C цепях.
Необходимо отметить, что форма напряжений и тока в исследуемых цепях существенно зависит от соотношения между постоянной времени цепи и длительностью импульса.