Тема: Относительная частота случайного события.
Класс: 9 класс.
Цели урока: рассмотреть основные понятия теории вероятности: ввести понятия «случайное событие», «относительная частота случайного события»; выработать умения решать простейшие задачи с использованием этих понятий.
Знания и умения: формирование умений и навыков решения задач на определение относительной частоты случайного события.
Учебная задача:
1.Формирование системы по изучению понятия события;
2.Формирование системы фактов «случайное событие», «относительная частота случайного события», «статистический подход» в курсе математики.
Ход урока.
I. Сообщение темы и цели урока.
II. Повторение и закрепление пройденного материала.
Для того чтобы постараться ответить на поставленный вопрос, давайте вспомним:
1.Что означает запись n!? Найдите значение выражения 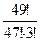 .
.
2.Что называется перестановкой из n элементов?
3.Что называется размещением из n элементов по k?
4.Что называется сочетанием из n элементов по k?
5.Запишите формулы.
III. Изучение нового материала.
Нам нередко приходится проводить наблюдения, опыты, участвовать в экспериментах или испытаниях. Часто подобные исследования заканчиваются некоторым результатом, который заранее предсказать нельзя.
Если открыть книгу наугад, то невозможно знать заранее, какой номер страницы вы увидите. Мы твердо знаем, что лето кончится, наступит осень, а затем зима. Но невозможно сказать заранее, будет эта зима теплой или холодной. Как правило, наблюдения или эксперимент определяются каким-то комплексом условий. Например, футбольный матч должен проходить по правилам.
Событием называется р езультат наблюдения, опыта, эксперимента.
|
|
Случайным событием называют такой результат наблюдения или эксперимента, который при соблюдении определенных условий может произойти, а может и не произойти.
Закономерности случайных событий изучает специальный раздел математики, который называется теорией вероятностей.
Событие случайное, если нельзя утверждать, что это событие в данных обстоятельствах непременно произойдет.
Представим, что выпущен 1000000 лотерейных билетов и разыгрывается один автомобиль. Можно ли, приобретя один лотерейный билет, выиграть этот приз? Конечно, можно, хотя это событие маловероятно. А если будут разыгрываться 10 автомобилей? Ясно, что вероятность выигрыша увеличится. Если же представить, что разыгрываются 999999 автомобилей, то вероятность выигрыша станет намного большей.
Следовательно, вероятности случайных событий можно сравнивать.
Люди давно заметили, что многие события происходят с той или иной, на удивление постоянной, частотой.
Начиная с ХVІІІ в. многие исследователи проводили серии испытаний с подбрасыванием монеты.
В таблице приведены результаты некоторых таких
| Исследователь | Количество подбрасываний монеты | Количество выпадений герба | Частота выпадения герба |
| Жорж Бюффон (1707–1788) | 0,5069 | ||
| Огастес де Морган (1806–1871) | 0,5005 | ||
| Уильям Джевонс (1835–1882) | 20 480 | 10 379 | 0,5068 |
| Всеволод Романовский (1879–1954) | 80 640 | 39 699 | 0,4923 |
| Карл Пирсон (1857–1936) | 24 000 | 12 012 | 0,5005 |
| Уильям Феллер (1906–1970) | 10 000 | 0,4979 |
По приведенным данным прослеживается четкая закономерность: при многократном подбрасывании монеты частота появления герба незначительно отклоняется от числа 0,5.Следовательно, можно считать, что вероятность события «выпадение герба» приблизительно равна 0,5. В каждом из рассмотренных примеров использовалось понятие частота случайного события. Эту величину мы вычисляли по формуле:
|
|
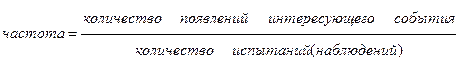
Далее по частоте мы оценивали вероятность события, а именно: вероятность случайного события приближенно равна частоте этого события, найденной при проведении большого количества испытаний (наблюдений).
Такую оценку вероятности случайного события называют статистической. Ее используют в разных областях деятельности человека: физике, химии, биологии, страховом бизнесе, социологии, экономике, здравоохранении, спорте.
Вводимые обозначения:
А – событие;
т – число испытаний, при которых произошло событие А;
п – общее число испытаний;
Р (A) = 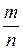 – относительная частота случайного события.
– относительная частота случайного события.
Проблемный вопрос: Почему важна относительная частота события?
Пример.
Иван попал в мишень 3 раза, Петр – 4. Кто из них лучше стреляет?
Можно ответить, что Петр – лучше, так как больше число попаданий. Но мы не знаем, сколько у каждого было попыток. Например, Иван сделал всего три выстрела и попал все три раза, относительная частота попадания Р (A) = 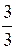 = 1. А Петр сделал серию из 20 выстрелов и попал всего четыре раза: Р (A) =
= 1. А Петр сделал серию из 20 выстрелов и попал всего четыре раза: Р (A) = 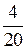 = 0,2.)
= 0,2.)
IV. Закрепление знаний
1. Событие А – появление нестандартной детали;
т = 12 – число нестандартных деталей;
п = 1000 – общее число деталей;
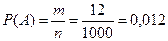 |
Ответ: 0,012
2.
Событие А – солнечный день;
|
|
т = 46 – число солнечных дней за указанный период;
п = 31+31=62 – общее число дней в указанном периоде;
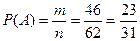 |
Ответ: 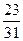
3.
а)
Событие А – появление в тексте буквы «в »;
т = 6 – количество букв «в » в тексте;
п = 164 – общее количество букв в тексте;
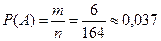 |
Ответ:0,037
б)
Событие А – появление в тексте буквы «м »;
т = 6 – количество букв «м » в тексте;
п = 164 – общее количество букв в тексте;
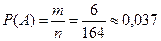 |
Ответ:0,037
V. Домашнее задание
П 14.5
1) Из 9 «А» класса, в котором 27 учеников, по жребию выбирают двух дежурных в столовую. Какова вероятность того, что дежурить будет ученик этого класса Иванов Дима?
2) Из класса, в котором учатся 15 девочек и 10 мальчиков, выбирают по жребию одного дежурного. Какова вероятность, что это будет мальчик?