Широко распространены реакции, в которых образуются и реагируют активные промежуточные частицы: атомы, свободные радикалы, лабильные комплексы, химически активные ионы и ионы-радикалы. Эти частицы настолько активно вступают в реакцию, что в системе очень быстро устанавливается динамическое равновесие. Начиная с некоторого времени — времени установления динамического равновесия — концентрация таких активных частиц квазистационарна, т.е. очень близка к концентрации, которая определяется равенством скоростей образования и расходования этих частиц.
Стационарная концентрация. При протекании в системе обратимой реакции, например, 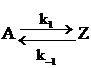 , концентрации реагентов стремятся к своим равновесным значениям: СA→a∞, CZ→z∞, которые при постоянных условиях сохраняются постоянными (стационарными). Концентрацию А можно рассматривать как стационарную и практически равную a∞, если (СA–a∞)<da∞, где da∞ — относительная погрешность в измерении СA. Поскольку разница СA–a∞ убывает экспоненциально во времени (СA–a∞)/a∞=e–t/τ*, то СA≈a∞ при t> ‑τ*ln da∞=7(k1+k -1)–1∞, если da∞=0,001. Таким образом, когда в системе протекают только обратимые реакции, стационарная концентрация реагентов устанавливается за время порядка 10 τ*.
, концентрации реагентов стремятся к своим равновесным значениям: СA→a∞, CZ→z∞, которые при постоянных условиях сохраняются постоянными (стационарными). Концентрацию А можно рассматривать как стационарную и практически равную a∞, если (СA–a∞)<da∞, где da∞ — относительная погрешность в измерении СA. Поскольку разница СA–a∞ убывает экспоненциально во времени (СA–a∞)/a∞=e–t/τ*, то СA≈a∞ при t> ‑τ*ln da∞=7(k1+k -1)–1∞, если da∞=0,001. Таким образом, когда в системе протекают только обратимые реакции, стационарная концентрация реагентов устанавливается за время порядка 10 τ*.
Квазистационарная концентрация. Если промежуточный продукт Х образуется со скоростью v1, а расходуется с константой скорости k2 (это может быть и сумма удельных скоростей его расходования), то его концентрация близка к квазиравновесной 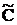 =v1/k2 для t>k2–1 и при условии dСX/dt<<dv1/dt.
=v1/k2 для t>k2–1 и при условии dСX/dt<<dv1/dt.
Примеры.
1) 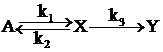 , равновесие устанавливается быстро. Пусть k1>k2>k3. Тогда приближенно можно считать концентрацию Х такой же, как в обратимой реакции
, равновесие устанавливается быстро. Пусть k1>k2>k3. Тогда приближенно можно считать концентрацию Х такой же, как в обратимой реакции 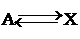 , т.е.
, т.е. 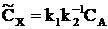 , а
, а 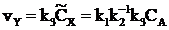 . Превращение А в Y в такой системе подобно реакции
. Превращение А в Y в такой системе подобно реакции 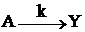 , где k=k1k2–1k3 и CY=(1–e–kt).Погрешность в вычислении CY при таком приближении равна концентрации Х. При строгом решении задачи
, где k=k1k2–1k3 и CY=(1–e–kt).Погрешность в вычислении CY при таком приближении равна концентрации Х. При строгом решении задачи 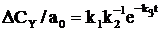 и при t=t1/2=k–1 ln 2 (период полупревращения А) относительная погрешность
и при t=t1/2=k–1 ln 2 (период полупревращения А) относительная погрешность 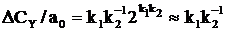 . При допустимой погрешности в 1% квазистационарное приближение можно использовать для случаев с k2≥100k1.
. При допустимой погрешности в 1% квазистационарное приближение можно использовать для случаев с k2≥100k1.
2) 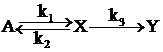 , общий случай (k1>k2 и k1>k3).
, общий случай (k1>k2 и k1>k3).
Приближенно считаем равными скорости образования и расходования Х: k1CA=(k2+k3) 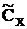 ,
, 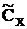 =k1(k2+k3)–1CA, а WY= –WA=k3
=k1(k2+k3)–1CA, а WY= –WA=k3 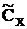 =k1k3(k2+k3)–1CA и CY=ao(1–e–kt), где k=k1(k2+k3)–1. Погрешность в вычислении CY равна DСY/ao=k1(k2+k3)–1
=k1k3(k2+k3)–1CA и CY=ao(1–e–kt), где k=k1(k2+k3)–1. Погрешность в вычислении CY равна DСY/ao=k1(k2+k3)–1 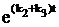 и при t=t1/2 DCY/ao
и при t=t1/2 DCY/ao 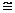 k1(k2+k3)–1.
k1(k2+k3)–1.
3) 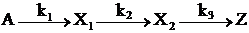 .
.
Квазистационарные концентрации Х1 и Х2 равны 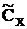 =k1k2–1CA, С2=k1k3–1CA. В квазистационарном приближении реакция протекает подобно реакции
=k1k2–1CA, С2=k1k3–1CA. В квазистационарном приближении реакция протекает подобно реакции 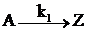 , CZ=ao(1–
, CZ=ao(1– 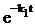 ). Погрешность в вычислении СZ в квазистационарном приближении
). Погрешность в вычислении СZ в квазистационарном приближении
DСZ/CA 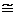 k1(k2–1+k3–1). При допустимой погрешности в 1% приближение применимо, когда (k2–1+k3–1)≤0,01 k1–1.
k1(k2–1+k3–1). При допустимой погрешности в 1% приближение применимо, когда (k2–1+k3–1)≤0,01 k1–1.
Из рассмотренных примеров видно, что в квазистационарном режиме скорости образования и расходования промежуточного продукта очень близки (почти равны), но во времени соотношение этих скоростей изменяется. В этом изменении и заключается отличие стационарного приближения от квазистационарного: концентрация C→C∞≠0 (C∞=const) и квазистационарна, если при t→∞ С→ 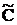 , но квазиравновесная концентрация
, но квазиравновесная концентрация 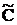 меняется во времени, так как изменяются условия динамического равновесия. Метод квазистационарных концентраций широко используют при анализе механизмов цепных, каталитических и энзиматических реакций.
меняется во времени, так как изменяются условия динамического равновесия. Метод квазистационарных концентраций широко используют при анализе механизмов цепных, каталитических и энзиматических реакций.