Степенные ряды
Функциональный ряд вида 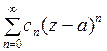 , где
, где 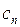 и
и  − заданные комплексные числа,
− заданные комплексные числа, 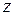 − комплексное переменное, называется степенным рядом, а
− комплексное переменное, называется степенным рядом, а 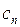 − коэффициентами степенного ряда.
− коэффициентами степенного ряда.
Будем рассматривать ряд  , где
, где 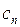 ,
, 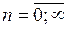 и
и 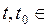 R (1)
R (1)
Сделав замену 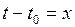 , получим ряд
, получим ряд 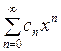 (2), исследование которого равносильно исследованию сходимости ряда (1).
(2), исследование которого равносильно исследованию сходимости ряда (1).
Теорема 1 (Абеля). Если степенной ряд сходится при 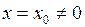 , то он сходится и притом абсолютно при
, то он сходится и притом абсолютно при 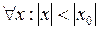 , а если он расходится при
, а если он расходится при  , то он расходится при
, то он расходится при 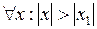 .
.
Доказательство. 1) Пусть 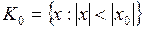 − интервал
− интервал 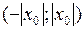 , и пусть
, и пусть 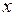 − произвольная точка этого интервала, т.е.
− произвольная точка этого интервала, т.е. 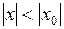 , поэтому
, поэтому 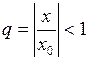 .
.
Так как ряд (2) по условию сходится в точке 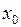 , то
, то 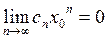 , откуда следует, что последовательность
, откуда следует, что последовательность 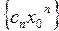 − ограничена, т.е.
− ограничена, т.е.
 :
: 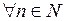
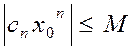 .
.
Тогда 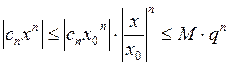 , где
, где  . Так как ряд
. Так как ряд 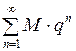 − сходится, то по признаку сравнения ряд
− сходится, то по признаку сравнения ряд 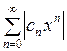 − сходится, т.е. ряд (2) сходится абсолютно в любой точке интервала
− сходится, т.е. ряд (2) сходится абсолютно в любой точке интервала 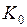 .
.
2) Пусть ряд (2) расходится в точке 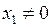 . Тогда он расходится в любой точке
. Тогда он расходится в любой точке  , так как в противном случае, по доказанному в пункте 1), ряд
, так как в противном случае, по доказанному в пункте 1), ряд 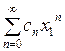 сходился бы.
сходился бы.
Следствие. Если ряд (2) сходится в точке  , то на отрезке
, то на отрезке 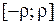 , где
, где  , этот ряд сходится абсолютно и равномерно.
, этот ряд сходится абсолютно и равномерно.
Доказательство. Если 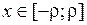 , то
, то 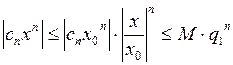 ,
,
где 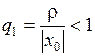 , причем
, причем  не зависит от
не зависит от 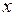 . По признаку Вейерштрасса, ряд (2) сходится абсолютно и равномерно на отрезке
. По признаку Вейерштрасса, ряд (2) сходится абсолютно и равномерно на отрезке 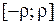 .
.
Теорема 2. Для всякого степенного ряда (2) существует R (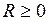 − число или
− число или 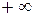 ), такое, что
), такое, что
а) если 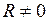 и
и  , то ряд (2) абсолютно сходится на интервале
, то ряд (2) абсолютно сходится на интервале 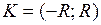 и расходится вне этого интервала;
и расходится вне этого интервала;
б) если 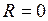 , то ряд (2) сходится только в одной точке
, то ряд (2) сходится только в одной точке  ;
;
в) если 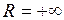 , то ряд (2) сходится на всей числовой прямой.
, то ряд (2) сходится на всей числовой прямой.
Доказательство. Пусть  − множество всех точек прямой, в которых ряд (2) сходится. Это непустое множество, т.к. в точке
− множество всех точек прямой, в которых ряд (2) сходится. Это непустое множество, т.к. в точке  ряд сходится. Если
ряд сходится. Если  − неограниченное множество, то ряд (2) сходится в любой точке
− неограниченное множество, то ряд (2) сходится в любой точке  числовой прямой. Действительно, возьмем точку
числовой прямой. Действительно, возьмем точку 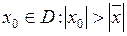 . По теореме Абеля, ряд (2) сходится в точке
. По теореме Абеля, ряд (2) сходится в точке  .
.
Пусть  − ограниченное множество. Если
− ограниченное множество. Если  содержит хотя бы одну точку, отличную от
содержит хотя бы одну точку, отличную от  , то обозначим
, то обозначим 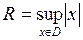 . По теореме Абеля, ряд (2) сходится на интервале
. По теореме Абеля, ряд (2) сходится на интервале 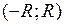 . Если
. Если 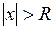 , тогда
, тогда 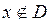 , и ряд (2) расходится вне этого интервала.
, и ряд (2) расходится вне этого интервала.
Замечание. На границе интервала сходимости ряд (2) может как сходиться, так и расходиться. На любом меньшем отрезке  ряд (2) сходится абсолютно и равномерно.
ряд (2) сходится абсолютно и равномерно.
Теорема 3. Если существует конечный или бесконечный 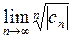 , то радиус сходимости ряда (2) вычисляется по формуле:
, то радиус сходимости ряда (2) вычисляется по формуле: 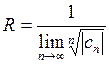 , а если
, а если
существует конечный или бесконечный  , то радиус сходимости ряда (2) вычисляется по формуле:
, то радиус сходимости ряда (2) вычисляется по формуле: 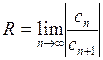 .
.
Доказательство. Докажем первую формулу. Обозначим  .
.
Пусть 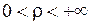 и пусть
и пусть 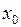 − произвольная точка интервала
− произвольная точка интервала  , т.е.
, т.е. 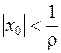 .
.
Рассмотрим 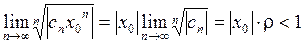 . Значит, по признаку Коши, ряд
. Значит, по признаку Коши, ряд 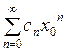 абсолютно сходится.
абсолютно сходится.
Если  лежит вне интервала
лежит вне интервала 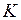 , тогда
, тогда  и
и 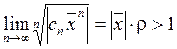 , и ряд
, и ряд 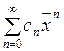 расходится. Значит, число
расходится. Значит, число 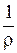 является радиусом сходимости.
является радиусом сходимости.
Формула верна и при  , и при
, и при 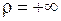 .
.
Вторая формула доказывается аналогично с помощью признака Даламбера.
Замечание 1. Пределы в теореме 3 могут не существовать. Но имеется универсальная формула Коши-Адамара для вычисления радиуса сходимости степенного ряда: 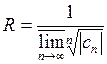 .
.
Замечание 2. Для степенного ряда 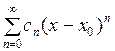 интервал сходимости имеет вид:
интервал сходимости имеет вид: 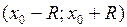 , а радиус сходимости совпадает с радиусом сходимости степенного ряда
, а радиус сходимости совпадает с радиусом сходимости степенного ряда 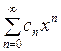 .
.
Свойства степенных рядов.
Теорема 1. Сумма степенного ряда в области сходимости есть функция непрерывная.
Теорема 2. Степенные ряды 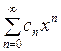 ,
,  и
и 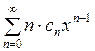 имеют один и тот же радиус сходимости.
имеют один и тот же радиус сходимости.
Теорема 3. Если ряд  имеет радиус сходимости
имеет радиус сходимости 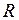 , то
, то
1) в интервале сходимости 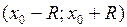 функция
функция 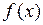 имеет производные любого порядка, получаемые почленным дифференцированием, т.е. функция
имеет производные любого порядка, получаемые почленным дифференцированием, т.е. функция 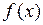 − бесконечно-дифференцируема;
− бесконечно-дифференцируема;
2) внутри интервала сходимости этот ряд можно почленно интегрировать, т.е. 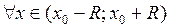 справедливо равенство:
справедливо равенство:
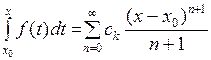 .
.
Ряд Тейлора
Если функция 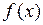 определена в некоторой окрестности точки
определена в некоторой окрестности точки 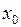 и имеет в точке
и имеет в точке 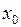 производные всех порядков, то степенной ряд
производные всех порядков, то степенной ряд
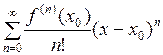 (1)
(1)
называется рядом Тейлора функции 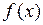 в точке
в точке 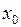 .
.
Вообще говоря, если 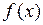 бесконечно дифференцируема в точке
бесконечно дифференцируема в точке 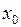 (и даже в некоторой окрестности этой точки), то нельзя утверждать, что составленный ряд Тейлора сходится при
(и даже в некоторой окрестности этой точки), то нельзя утверждать, что составленный ряд Тейлора сходится при 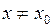 к функции
к функции 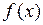 .
.
Пусть 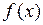 − бесконечно-дифференцируема в точке
− бесконечно-дифференцируема в точке 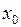 . Обозначим
. Обозначим
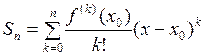 ,
, 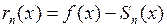 ,
,
и назовём 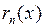 остаточным членом формулы Тейлора для функции
остаточным членом формулы Тейлора для функции 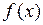 в точке
в точке 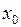 . Если существует
. Если существует  , то это означает, что ряд (1) сходится к функции
, то это означает, что ряд (1) сходится к функции 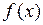 в точке
в точке 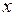 , т.е.
, т.е. 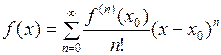 .
.
Теорема 1. Если функции 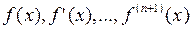 непрерывны на интервале
непрерывны на интервале 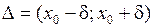 , где
, где  , то для
, то для  остаточный член формулы Тейлора для функции
остаточный член формулы Тейлора для функции 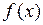 в точке
в точке 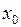 можно представить:
можно представить:
а) в интегральной форме:  ;
;
б) в форме Лагранжа: 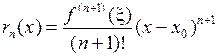 , где
, где 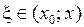 ;
;
в) в форме Пеано: 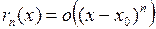 при
при 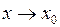 .
.
Теорема 2. Если функция 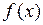 и все её производные ограничены в совокупности на некотором интервале
и все её производные ограничены в совокупности на некотором интервале 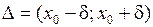 , т.е.
, т.е.
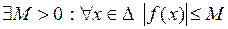 ,
, 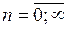 , то
, то
функция 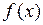 представима в виде сходящегося к ней в каждой точке интервала
представима в виде сходящегося к ней в каждой точке интервала 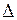 ряда Тейлора (1), т.е.
ряда Тейлора (1), т.е.

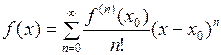 .
.
Доказательство. Пусть 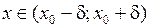 , тогда
, тогда
 .
.
Так как 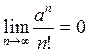 ,
, 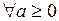 , то получаем, что
, то получаем, что 
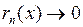 при
при 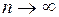 . Значит, ряд Тейлора (1) сходится к функции
. Значит, ряд Тейлора (1) сходится к функции 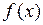 .
.
Замечание. Теорема 2 остается верна, если условие её теоремы заменить на 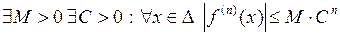 ,
, 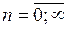 .
.
Разложение элементарных функций в ряд Тейлора
Если 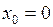 , то ряд Тейлора принимает вид:
, то ряд Тейлора принимает вид: 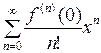 . (2)
. (2)
Этот ряд называется рядом Маклорена.
Найдём разложение основных элементарных функций в ряд Маклорена.
1) 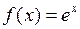 .
. 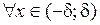 ,
, 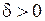 выполняются неравенства:
выполняются неравенства:
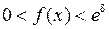 ,
, 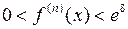 ,
, 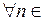 N.
N.
По теореме 2, ряд (2) для функции 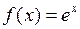 сходится к этой функции на интервале
сходится к этой функции на интервале 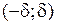 при
при 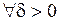 , т.е. радиус сходимости этого ряда
, т.е. радиус сходимости этого ряда  .
.
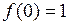 ,
,  , поэтому
, поэтому  ,
,  .
.
Т.к.  ,
, 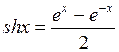 , то
, то
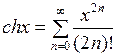 ,
, 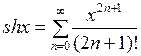 .
.
2) 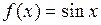 . Тогда
. Тогда 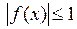 ,
, 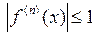 ,
, 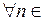 N.
N.
Значит, ряд Маклорена для 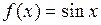 сходится к этой функции
сходится к этой функции 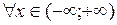 , т.е. радиус сходимости этого ряда
, т.е. радиус сходимости этого ряда 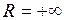 .
.
 ,
,  ,
,  ,
,  N. Поэтому
N. Поэтому
 ,
, 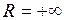 .
.
Аналогично рассуждая, получим:
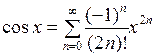 ,
, 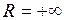 ,
,  ,
,  ,
,
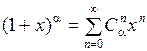 , где
, где  ,
, 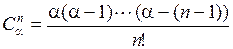 ,
,  ,
,
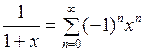 ,
,  ,
,  ,
,  .
.