Другим известным методом минимизации считается метод минимизирующих карт Карно-Вейча, позволяющий сразу получать тупиковые формы.
Метод основан на представлении булевой функции в виде карты (таблицы), в которой каждой ячейке соответствует один входной набор переменных, причем любые две соседние ячейки имеют коды, отличающиеся значением только одного разряда, т.е. склеиваемые коды.
Покажем принцип построения минимизирующих карт.


| x 2 | ||||||
| 1 0 | 0 00 | 1 01 | ||||
| x 1 | 0 1 | x 1 | 1 10 | 1 11 |
a) карта для булевой функции б) карта для булевой функции
от одной переменной от двух переменных


 x 2
x 1 x 2
x 1
| ||||||||
| x 1 | x 2 | x 3 | f 3 | |||||
| в) карта для булевой функции от двух переменных | ||||||||
 x 2 x 3
x 1 x 2 x 3
x 1
| x 3 | ||||
| x 2 | |||||
| x 1 |  1 1
|
г) таблица истинности и карта для функции от трех переменных
Рис. 5
Для всех карт каждой ячейке соответствует входной набор переменных и значение функции на данном наборе. На рис.5 а и 5 б значения переменных входных наборов показаны через покрытие ячеек переменными; в покрытой области x i =1, в непокрытой x i =0. На рисунке в указаны коды строк и столбцов, на рисунке г – обоими способами.
Вместо указания в каждой ячейка ее двоичного кода, можно указать его десятичное значение. Переменные, кодирующие строки карты можно использовать в качестве кодов столбцов и наоборот как на рис. 6.
 |  | ||
| х3х4 х1х2 | х1х2 х3х4 | |||||||||
Рис. 6. Карты с различным кодированием строк и столбцов.
Отличие этих двух карт в построчной или постолбцовой нумерации ячеек не меняет их основного принципа – соседнего кодирования ячеек.
Покажем применение карт для минимизации функции  :
:

| 
| 
| 
|
  0 0
| ||||
Рис. 7. Таблица истинности и карта Карно-Вейча для функции 
Соседние ячейки, содержащие 1 (или 0)в количестве 2К, объединяются контурами прямоугольной или квадратной формы и описываются отдельными простыми импликантами для получения ТДНФ (или имплицентами – для ТКНФ).
Каждый контур должен охватывать максимально возможное количество ячеек с 1 (или 0). Контурами должны быть покрыты все 1 (или 0). При правильном выборе контуров тупиковая форма функции 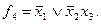
Функция может быть задана перечислением десятичных эквивалентов ее значений. Для полностью определенных функций достаточно задать множество входных наборов, на которых функция равна только 1 или только 0.
 или
или 
  1 1
| ||||||||


 задана конституентами 1, которыми и заполняется карта для
задана конституентами 1, которыми и заполняется карта для  . Все остальные наборы в полностью определенной функции можно не указывать, так как все они равны 0. После оклеивания по карте Карно-Вейча по 1 наборам получаем
. Все остальные наборы в полностью определенной функции можно не указывать, так как все они равны 0. После оклеивания по карте Карно-Вейча по 1 наборам получаем  в форме ТДНФ. Те же рассуждения справедливы при получении ТКНФ для
в форме ТДНФ. Те же рассуждения справедливы при получении ТКНФ для  .
.  и
и  являются при этом одной и той же функцией
являются при этом одной и той же функцией  =
=  , заданной разными конституентами.
, заданной разными конституентами.
Пример 4. Минимизировать функцию  .
.
Определим количество переменных функции  . Так как
. Так как 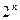 – количество входных наборов функции от n – переменных, то
– количество входных наборов функции от n – переменных, то  , где К – самый большой десятичный эквивалент двоичного входного набора.
, где К – самый большой десятичный эквивалент двоичного входного набора.
n=4, карта содержит 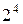 ячеек.
ячеек.
 |
 1 1
| |||

| |||
 1 1
|
ТДНФ: 
При использовании метода Квайна-Мак-Класки возникает еще один промежуточный этап между совершенной и тупиковой формами. Это этап получения сокращенной формы. При автоматизированном способе минимизации он неизбежен. Покажем для последнего примера этот промежуточный этап на минимизирующей карте штриховыми контурами.
 |
 1 1
| |||

| |||
 1 1
|
ДСНФ: 
Как видно, эти контуры не являются обязательными для обеспечения покрытия всех 1 функции и при использовании метода Квайна-Мак-Класки удаляются посредством импликантной таблицы.
3.3. Понятие интервала функции.
Представим БФ в виде гиперкуба, каждой вершине которого соответствует взаимнооднозначно входной двоичный набор. Все вершины упорядочены по ярусам. В i -й ярус входят вершины, с i -м количеством единиц в своих наборах. Вершины соединены ребром, если соответствующие двоичные наборы отличаются только одним разрядом (конъюнкции этих наборов могут быть склеены).
Вершины, образующие гиперкубы, кубы, грани, ребра или просто отдельные вершины, в которых  , порождают единичные интервалы этой функции. Пример на рис. 7 для функции
, порождают единичные интервалы этой функции. Пример на рис. 7 для функции  .
.
Вершины, образующие гиперкубы, кубы, грани, ребра или просто отдельные вершины, в которых  , порождают нулевые интервалы этой функции.
, порождают нулевые интервалы этой функции.


 3 ярус 1 111
3 ярус 1 111
 | |||
 | |||


 110 011
110 011




 2 ярус 1 0 101 0
2 ярус 1 0 101 0
 |


 100 001
100 001

 1 ярус 1 1 010 0
1 ярус 1 1 010 0

 0 ярус 1 000
0 ярус 1 000
Рис. 7. Функция в виде гиперкуба с единичными интервалами – гранью и ребром.
Единичный интервал Ia называется максимальным, если не найдется другого единичного интервала Ib, включающего в себя Ia.
Единичные интервалы:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Максимальные интервалы: 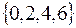 и
и  .
.
Конъюнкция, соответствующая максимальному единичному интервалу функции, является простой импликантой этой функции. Таким образом, выражение, составленное в виде дизъюнкции максимальных интервалов функции, будет его сокращенной ДНФ.
Переход от совершенной формы к сокращенной произошел путем попарного сравнения конституент соседних ярусов, что существенно сократило число сравнений (в отличие от количества сравнений по принципу «каждая с каждой», равному  , где К – количество конституент).
, где К – количество конституент).
3.4. Слабоопределенные БФ.
Слабоопределенные или неполностью определенные БФ характеризуются следующими признаками:
1) число переменных n велико;
2) количество конституент 1 и 0 намного меньше 
Так как для части входных наборов значения функции могут быть любыми, то при выполнении минимизации слабоопределенных функций сначала требуется их доопределение, причем такое, которое не противоречит цели минимизации – получению наиболее краткого (простого) выражения функции. То есть при минимизации слабоопределенных функций добавляется дополнительный этап – доопределение неопределенных состояний или мажорирования исходной функции.
Этапы минимизации БФ. Табл. 6
| Полностью определенные БФ | Слабоопределенные БФ |
| 1. Получение сокращенной формы. 2. Получение тупиковых форм. 3. Выбор среди тупиковых минимальной или кратчайшей форм. | 1. Получение сокращенной формы исходной функции. 2. Получение сокращенной формы мажорирующей функции. 3. Получение тупиковых форм. 4. Выбор среди тупиковых форм. |
Покажем минимизацию слабоопределенной функции на примере, причем для наглядности выберем функцию от четырех переменных, чтобы проследить этапы минимизации по карте Карно-Вейча.
Дана 
| x 4 | x 4 | x 4 | ||||||||||||||||||
| x 3 | x 3 | x 3 | ||||||||||||||||||
 
| ||||||||||||||||||||
  
| - | - | - | |||||||||||||||||
  x 2
x 2
| - | x 2 | x 2 | |||||||||||||||||
| x 1 | - | - | - | x 1 | x 1 | |||||||||||||||
  
| - | - | ||||||||||||||||||
| а) | б) | в) |
Рис. 8. а) функция f с выделенными исходными единичными и нулевыми интервалами;
б) и в) варианты доопределения f в виде мажорирующих ее f ’ и f ”.
1) Получим сокращенную форму исходной функции любым, известным способом.

2) Получим сокращенную форму, состоящую из максимальных единичных интервалов за счет доопределения в 1 некоторых неопределенных состояний (доопределение в 1 всех неопределенных состояний может быть далеко не самым удачным вариантом как, например, в нашем случае), для чего используем таблицу различий.
В таблице различий строками являются единичные интервалы, а столбцами – нулевые интервалы исходной функции  . Клетки таблицы заполняют последовательностями 1 и 0, полученными в результате поразрядного сложения по модулю 2 соответствующих разрядов строки и столбца:
. Клетки таблицы заполняют последовательностями 1 и 0, полученными в результате поразрядного сложения по модулю 2 соответствующих разрядов строки и столбца:
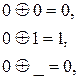
| 
| 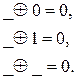
|
Таблица различий. Табл. 7
| Единичные интервалы | Нулевые интервалы | ||
| 011_ | |||
| a b c d | _ | ||
| a b c d | _ |
Разряды единичных интервалов идентифицированы буквами a,b,c,d. Таблица различий позволяет определить, какие переменные исходной конъюнкции (исходного единичного интервала) войдут в мажорирующий (максимальный интервал): те, по которым есть различие в знаке разряда. Если оставить в мажорирующей конъюнкции соответствующий разряд, то в 1 определяются те неопределенные состояния, которые этому разряду соответствуют.
Единичный интервал 0_00 имеет различие с нулевым интервалом 011_ в разряде с. Для обеспечения непересечения доопределяемой области с нулевой  обязательно будет присутствовать в мажорирующей конъюнкции. Единичный интервал 0_00 также имеет различие с нулевым интервалом 1101 в двух разрядах: a и d. Для обеспечения непересечения доопределяемой области с нулевой включим в мажорирующую конъюнкцию
обязательно будет присутствовать в мажорирующей конъюнкции. Единичный интервал 0_00 также имеет различие с нулевым интервалом 1101 в двух разрядах: a и d. Для обеспечения непересечения доопределяемой области с нулевой включим в мажорирующую конъюнкцию 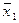 , либо
, либо  . Иллюстрация на рис.
. Иллюстрация на рис.
| x 4 | x 4 | ||||||||||||||
| x 3 | x 3 | ||||||||||||||
| x 2 | x 2 | ||||||||||||||
| x 1 | x 1 | ||||||||||||||
а) доопределение в 1 области 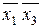 (или (или  мажорирует мажорирует  ). ).
|
б) доопределение в 1 области  (или (или  мажорирует мажорирует  ). ).
| ||||||||||||||
Рис. 9. Мажорирование конъюнкции  .
.
Итак, по единичному интервалу 0_00 получаем покрытие  , то есть два варианта максимальных единичных интервалов:
, то есть два варианта максимальных единичных интервалов:  ,
, 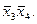
По единичному интервалу 101_ получаем покрытие  Так как покрытие
Так как покрытие  короче, чем
короче, чем 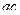 , то по интервалу 101_ выбираем только
, то по интервалу 101_ выбираем только  , то есть
, то есть  .
.
СДНФ мажорирующей функции:  :
:

3) Определим все варианты тупиковых форм  по импликантной таблице, где в качестве простых импликант будут максимальные единичные интервалы
по импликантной таблице, где в качестве простых импликант будут максимальные единичные интервалы  , а вместо конституент единицы – единичные интервалы функции
, а вместо конституент единицы – единичные интервалы функции  (таблица 8).
(таблица 8).
Табл. 8
| Иденти-фикаторы | Максимальные единичные интервалы | Единичные интервалы функции f. | |
| 0 _ 0 0 | 1 0 1 _ | ||
| a |  (0 _ 0 _) (0 _ 0 _)
| X | |
| b |  (_ _ 0 0) (_ _ 0 0)
| X | |
| c |  (_ 0 _ _) (_ 0 _ _)
| X |
Имеем покрытие П импликантной таблицы:
 .
.
Тупиковых форм две (ac и bc):
 .
.
4) Полученные тупиковые формы  , мажорирующие
, мажорирующие 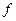 , идентичны, так как имеют равную сложность
, идентичны, так как имеют равную сложность  и цену по Квайну
и цену по Квайну  и, следовательно, обе являются одновременно минимальными и кратчайшими.
и, следовательно, обе являются одновременно минимальными и кратчайшими.
На основании принципа двойственности все изложенные выше методы минимизации в классе ДНФ можно распространить и на класс КНФ. В таблице различий для определения покрытия нулевого интервала поменяем местами строки и столбцы. В импликантной таблице вместо простых импликант (максимальных единичных интервалов) строками станут простые имплиценты (максимальные нулевые интервалы), а столбцами конституенты нуля (нулевые интервалы) функции.
Задача 2. Для игрушки пирамиды, состоящей из 3-х колец различного диаметра, определить все возможные сочетания раскраски колец, если нижнее кольцо может быть раскрашено в фиолетовый, синий или зеленый цвет, среднее кольцо – в желтый, белый или голубой, а верхнее – только в красный.


 Решение. Если известно, что
Решение. Если известно, что
III пирамида обязательно состоит из
трех колец, то объединим три
II обязательные части конструкции
I функцией конъюнкция:
 .
.
При этом каждая из частей имеет свою многовариантность раскраски  ,
, 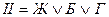 ,
,  Обобщенная структура раскраски будет представлять собой форму КНФ:
Обобщенная структура раскраски будет представлять собой форму КНФ:
 , а переход к форме ДНФ после раскрытия скобок покажет все возможные сочетания раскрасок:
, а переход к форме ДНФ после раскрытия скобок покажет все возможные сочетания раскрасок:
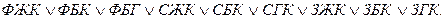 Всего 9 вариантов.
Всего 9 вариантов.
Контрольные вопросы и задания
1) Доказать тождество
___ _ _______ _ _ _
х1х2х3Úх2(х1Úх3)Úх2=х1Úх2Úх3
2) Привести выражения к формам ДНФ и КНФ
_________
_ _ ________
а) х1Úх2х3Úх2Ú (х1Úх3) х2
_____________
б) х1Úх2Úх3(х1Úх2)Úх3
с)  .
.
3) Минимизировать функции, заданные конституентами единицы или нуля по методу Квайна - Мак Класки:
f1=(1,3,5,7,8,10,14,15)|1; f2=(0,2,4,5,6,7,13,15)|0
4) Минимизировать функции по картам Карно-Вейча
| х1х2х3х4 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 | f1 | f2 | х1х2х3 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 | f3 | f4 |
| 5) Булева алгебра: булевы функции, определение, способы задания. 6) Основные законы алгебры логики |
| 7) Нормальные формы булевых функций. Алгоритм приведения к нормальным формам. 8) Совершенные формы булевых функций. Предельное разложение Шеннона |
| 9) Минимизация булевых функций. Карты Карно-Вейча. |
| 10) Метод Квайна – Мак Класки |
СПИСОК ЛИТЕРАТУРЫ
Основная литература
1. Горбатов В.А. Фундаментальные основы дискретной математики. М.: Наука. Физматлит.1999. – 544с.
или
2. Горбатов В.А. Основы дискретной математики. М.: Высшая математика 1986. – 311с.
3. Коршунов Ю.М. Математические основы кибернетики М: Энергоатомиздат 1987
4. Яблонский С.В. Введение в дискретную математику. М.: Высшая школа, 2001, 384с.
5. Петухин В.А. Дискретная математика. https://www.isu.ru/~slava/do/disc/curshome.htm 1999