Е.В. Королева
КОНСПЕКТ ЛЕКЦИЙ ПО ДИСЦИПЛИНЕ
«ОСНОВЫЛОГИЧЕСКОГО УПРАВЛЕНИЯ»
Часть I
БУЛЕВА АЛГЕБРА
Для студентов направлений 151900, 151000, 150900
 Ижевск 2008
Ижевск 2008
СОДЕРЖАНИЕ:
Введение 3
МАТЕМАТИЧЕСКАЯ ЛОГИКА 7
Булева алгебра 9
Доказательства равенства булевых функций 11
Основные законы булевой алгебры 12
О количестве двоичных наборов булевых функций и количестве булевых функций от n-переменных 13
Системы и базисы булевых функций 15
Критерий полноты систем булевых функций
Поста-Яблонского 16
НОРМАЛЬНЫЕ ФОРМЫБФ 20
Алгоритм приведения БФ к нормальным формам 22
Совершенные нормальные формы. Разложение Шеннона 23
Приведение к совершенным формам ДНФ и КНФ 24
Сокращенные и тупиковые нормальные формы 24
МЕТОДЫМИНИМИЗАЦИИ БУЛЕВЫХ ФУНКЦИЙ 28
Метод Квайна – Мак-Класки 28
Минимизация по картам Карно-Вейча 29
Понятие интервала функции 33
Слабоопределенные БФ 35
Контрольные вопросы 39
Список литературы 40
ВВЕДЕНИЕ
Наука об управлении - кибернетика – это наука об общих законах представления, хранения, передачи и обработки информации. История этой науки насчитывает всего несколько десятилетий (с 1948 года, когда была выпущена в свет книга американского ученого Норберта Винера «Кибернетика или управление и связь в животном и машине»), а вклад в ее развитие и становление внесли сотни талантливых ученых мира, среди которых ее основатель Н. Винер, выдающиеся советские ученые А.И. Берг, В.М. Глушков, А.А. Ляпунов.
Наиболее коротко кибернетику можно определить как науку об управлении (которое и является предметом ее изучения) в различных системах любой физической природы. Но, в отличие от многих других наук, также изучающих управление, кибернетика рассматривает его в математическом и физическом аспектах.
В период второй мировой войны, Н. Винер участвовал в работе над проектом правительства США по проблеме управления зенитным огнем. Эти работы завершились созданием нового оружия с радиолокационным наведением. В основу этой работы был положен принцип обратной связи (отрицательной и прямой), который заключался в использовании информации, поступающей из окружающего мира для изменения поведения машины. Винер показал, что именно благодаря обратной связи все живое приспосабливается к окружающей среде и взаимодействует с ней, то есть, в конечном счете, обучается. Для него было абсолютно ясно, что многие концептуальные схемы, определяющие поведение живых организмов при реакции на ситуацию должны быть аналогичны схемам управления в сложных технических системах, что социальные и экономические модели управления могут быть проанализированы с помощью тех же логико-математических аппаратов, которые разработаны для управления техническими системами.
Именно эти идеи показались крамольными в бывшем СССР. В силу существовавшей тогда идеологической доктрины, кибернетика в 50-х годах ХХ века была воспринята как наука, противоречащая основным принципам марксизма-ленинизма, например несводимости «высших» форм существования к «низшим», формализме (формальная логика), а, следовательно, идеализме, проникающем в общественное сознание через математику. Однако, идеи кибернетики нашли отклик у авторитетных ученых, таких, как А.И.Китов – один из первых отечественных специалистов по применению вычислительных машин в военной области, А.А.Ляпунов – выдающийся математик, С.Л.Соболев – математик, занимавшийся теорией создания атомной бомбы. Уже к концу 50-х советская наука получила ряд результатов, стоящих на уровне мировых достижений:
- Была разработана теория логического анализа и синтеза релейно-контактных и функциональных схем, где аппарат математической логики был использован в области технических наук. Возникли две научные школы О.Б.Лупанова и С.В. Яблонского, занимавшиеся теорией дискретных управляющих устройств и методов инженерного проектирования устройств такого типа (в т.ч. схем, узлов, устройств вычислительной техники);
- А.А. Ляпунов предложил операторный метод для описания программ, который позволил создать теорию синтаксических структур программ;
- А.А. Ляпуновым была сформулирована постановка задачи автоматизации программирования, воплощенная в первых отечественных трансляторах;
- М.Л. Цетлин впервые рассмотрел возможности моделирования с помощью простейших технических средств сложных форм поведения, что послужило началом создания теории коллективного поведения технических систем, намного опередившей аналогичные исследования в других странах.
Кроме перечисленных выше имен, следует особо назвать В.М. Глушкова, автора методов логического синтеза цифровых автоматов, выдающегося математика А.А. Маркова и А.И. Берга, выдающегося организатора науки, занимавшего пост заместителя министра обороны СССР по радиоэлектронике в 1953-1957 годах. Этим перечнем, безусловно, не исчерпывается список выдающихся ученых, внесших значительный вклад в формирование современных знаний.
Винер разработал теории машинного и человеческого разума, опираясь на идею обратной связи, которая сразу же стала объединяющей в исследованиях представителей различных наук.
Кибернетика (с греческого – «рулевой») в свое время очертила круг задач по проблемам управления и связи, решение которых не представлялось возможным в рамках ни одной из существующих наук. Такие задачи могли возникнуть в физике, математике, философии, социологии, психологии, вычислительной технике, электротехнике и т.д., то есть принадлежать одной конкретной науке, а вот решение представлялось возможным лишь на стыке наук. Подобные задачи Винер называл кибернетическими, а их общие специфические свойства (управление, связь) по сути, и являются кибернетикой.
Существуют такие общенаучные категории как «энергия» и «информация». Понятие «управление» перешло в общенаучную категорию не так давно, когда определилась его сущность:
движение или действие больших масс, передача, преобразование больших количеств энергии направляются и контролируются при помощи небольших количеств энергии, несущих информацию.
Такое определение справедливо для любых объектов, где есть управление – компьютер, социальное общество, живой организм и т.д.
По сложившейся к настоящему времени традиции, понятие «кибернетической управляющей системы» более узко, в сравнении с понятием просто «управляющей системы» к которым могут принадлежать объекты по традиции и по существу не относящиеся к кибернетическим: автомобильный карбюратор в системе подачи топлива регулирует впрыск топлива, температурное реле и т.д.
Для определения понятия кибернетической системы выделяют три признака:
q дискретность;
q сложность;
q многозначность представлений.
По определению Ляпунова, кибернетика – это «наука об общих закономерностях строения управляющих систем и течения процессов управления» и, следовательно, связана с вопросами кодирования, хранения, передачи, переработки, воспроизведения информации и устройствами для осуществления этих функций.
Наукообразующим вопросом для кибернетики, по Ляпунову, является вопрос о взаимоотношении мышления и возможностей вычислительной машины. Сами же мышление и вычислительная машина представляют собой примеры управляющих систем крайних типов: неформализованной и строго формализованной. Вопрос считается изученным, если функционирование управляющей системы полностью формализовано и может быть смоделировано в универсальной вычислительной машине. Этим и занимается математическая кибернетика – синтезом алгоритмов, разработкой способов их описания и оценки производительности, принципами их материальной реализации. Кроме того, существуют «экспериментальные» методы исследования - наблюдение, статистический анализ, логический анализ, машинный эксперимент. Все эти методы (математические и «экспериментальные») применяются при решении задач основных направлений кибернетики:
1. системы сигналов управления и обратной связи – языки и способы кодирования информации;
2. процессы переработки информации;
3. методы анализа и синтеза управляющих систем;
4. помехоустойчивость в процессах управления.
Как сказано выше, кибернетика возникла на стыке многих наук как средство решения возникающих в них вопросов, среди которых самым главным, глобальным, можно считать вопрос о механизме процесса мышления в теоретическом и практическом смысле – могут ли машины «мыслить», можно ли создать искусственный интеллект? Размышление над ними ставит новые вопросы: что такое мышление, оно присуще только человеку и живым организмам, или машине в том числе, что такое процесс обучения и могут ли машины обучаться.
Совокупность научных направлений, относящихся к кибернетике, именуют, кроме того, «компьютерными науками», «информатикой», «прикладной математикой» в силу исторически сложившихся традиций. К настоящему времени основными областями исследований кибернетики (или информатики) считают следующие:
- теория алгоритмов (формальные модели алгоритмов, проблемы вычислимости, сложность вычислений и т.д.)
- логические модели (дедуктивные системы, сложность вывода, нетрадиционные исчисления: индуктивный и абдуктивный вывод, вывод по аналогии, правдоподобный вывод, немонотонные рассуждения и т.п.)
- искусственный интеллект (представление знаний, вывод на знаниях, обучающиеся, экспертные системы и т.п.)
- бионика (математические модели в биологии, бихевиористические (поведенческие) модели, генетические системы и т.п.)
- теория роботов (автономные роботы, представление знаний о мире, децентрализованное управление, планирование целесообразного поведения и т.п.)
- компьютерная лингвистика (модели языка, анализ и синтез текстов, машинный перевод и т.п.)
- системы человеко-машинного взаимодействия (модели дискурса, распределение работ в смешанных системах, организация коллективнах процедур, деятельность в телекоммуникационных системах и т.п.)
- нейроматематика и нейросистемы (теория формальных нейронных сетей, использование нейронных сетей для обучения, нейрокомпьютеры и т.п.)
Эти научные направления возникли не одновременно, а по мере накопления моделей, методов их применения на задачах различных типов, развития компьютеров.
В предлагаемом читателю учебном пособии из всех вопросов кибернетики рассматриваются основы логического управления: математическая логика, теория множеств, теория графов.
МАТЕМАТИЧЕСКАЯ ЛОГИКА
Математическая логика – раздел математики, изучающий математические доказательства и вопросы обоснования математики. История математической логики идет от древних цивилизаций – древнегреческой, древнеиндийской, древнекитайской - каждая из них внесла свой особый вклад в развитие этой науки.
Так, в Китае наиболее развитым оказался раздел о системах и базисах булевых функций, но он не имел практического применения на тот период времени и стал развиваться только в эпоху компьютеров, когда возникла необходимость в определении элементной базы для создания логических устройств компьютера. В Индии и Греции получил наибольшее развитие раздел исчисления высказываний благодаря использованию логики в судебной практике. Множество существовавших когда-то научных школ оказались тупиковыми в силу того, что избранное ими направление не могло быть востребовано практикой, не имело прикладного значения на тот период времени.
По существу возврат к математической логике произошел в конце 18 – 19 веках нашего времени, когда проблемы математики потребовали для своего решения достаточно специфические приемы, отсутствовавшие тогда в ее арсенале. Например, открытие рядов повлекло за собой исследования в теории множеств, изучение законов математических доказательств – к исследованиям исчислений высказываний и предикатов.
Принято считать, что наибольший вклад в формирование современной математической логики как науки внес английский математик Джордж Буль (1815-1864), который решал задачу «алгебраизации логики». Природа математики, любого математического исчисления им понималась, как «метода, базирующегося на употреблении символов, законы, комбинации которых нам известны», где результат математического анализа «зависит не от истолкования символов, а исключительно от законов их комбинации».
Если философское понимание логики, как теории искусства рассуждения, целью которой является систематизация принципов правильного рассуждения и средством - изучение мышления как способа познания объективного мира, «тех его форм и законов, в которых происходит отражение мира в процессе мышления», то в математическом смысле она рассматривается более узко. [Гетманова].
Основная задача математической логики – формализация знаний и рассуждений. Наиболее легко формализуемые знания – математические и потому математическая логика – наука о математике, или метаматематика. Центральным понятием математической логики является «математическое доказательство». Действительно, «доказательные» (иначе говоря, дедуктивные) рассуждения – единственный вид признаваемых в математике рассуждений. Рассуждения в математической логике изучаются с точки зрения формы, а не смысла. По-существу, рассуждения моделируются чисто «механическим» процессом переписывания текста (формул). Такой процесс называют выводом. Говорят еще, что математическая логика оперирует только синтаксическими понятиями.
Однако если бывает нужно соотнести рассуждения с действительностью или представлениями о ней, то есть определить смысл формул и их вывода, то используют термин семантика (синоним слова «смысл») и чётко разделяют синтаксис и семантику.
Когда же действительно исследуют только форму (синтаксис), используют термины «формальная система», «исчисление формальных грамматик», «формальная теория» или «аксиоматика».
Объектом формальных систем являются последовательности символов, с помощью которых записываются формулы.
Научная теория, изучающая свойства знаковых систем, т.е. систем конкретных или абстрактных объектов, каждому из которых соответствует некоторое значение, называется семиотикой.
Знаковыми системами являются естественные и искусственные языки, системы сигнализации, системы состояний входных и выходных сигналов и т.п.
Самым первым и наиболее простым для понимания разделом математической логики является булева алгебра, лежащая в основе всех дальнейших построений математической логики. Рассмотрим булеву алгебру в двузначной логике.
БУЛЕВА АЛГЕБРА
Булеву алгебру составляют два множества – множество операторов или булевых функций и множество значений, к которым эти операторы применяются. В двузначной логике множество значений состоит из множеств {0, 1} или {И, Л}, а множество функций из некоторого набора функций f j.
Булевой функцией (БФ) или функцией алгебры логики f j(x1, x2, … xn) называется отображение n-мерного пространства {0, 1}n значений аргументов в одномерное пространство {0, 1} значений функции под действием f i:
f j
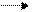 {0, 1}n {0, 1}.
{0, 1}n {0, 1}.
Таким образом, область определения БФ – n-мерное пространство {0, 1}n, где n – количество переменных функции, а область значений БФ – одномерное пространство {0, 1}.
По количеству переменных различают функции:
q ноль-местные - 0, 1;
q одноместные -  или
или  ;
;
q двухместные х1&x2 или х1Úх2;
q n -местные - # (x1,x2,…xn).
Существует несколько способов задания БФ:
· в табличном представлении;
· через перечисление десятичных эквивалентов двоичных наборов;
· в виде логического выражения.
В табличном представлении для каждого i-го набора входных переменных в таблице указано значение функции на этом наборе (рис. 1).
| Десятичный эквивалент i | x1x2x3 | fi |
| 0 0 0 | ||
| 0 0 1 | ||
| 0 1 0 | ||
| 0 1 1 | ||
| 1 0 0 | ||
| 1 0 1 | ||
| 1 1 0 | ||
| 1 1 1 |
Рис.1 Булева функция f в табличном представлении
При перечислении десятичных эквивалентов двоичных наборов достаточно перечислить только единичные или только нулевые наборы данной функции. Функция с рис.1, задана таким способом -  =(0,2,6,7) 1. Оставшиеся наборы -1,3,4,5 – считаем определенными в 0.
=(0,2,6,7) 1. Оставшиеся наборы -1,3,4,5 – считаем определенными в 0.
Для задания функции в виде логического выражения, т.е. через другие БФ, например  =
= 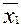
 Ú
Ú  , где использованы функции &,Ú,Ø, необходимо условиться о работе этих функций. Приведем таблицы истинности функций &-конъюнкции, Ú-дизъюнкции, Ø-отрицания:
, где использованы функции &,Ú,Ø, необходимо условиться о работе этих функций. Приведем таблицы истинности функций &-конъюнкции, Ú-дизъюнкции, Ø-отрицания:
Таблица 1 Таблица 2 Таблица 3
&-конъюнкция Ú-дизъюнкция Ø-отрицание
логическое «И» логическое «ИЛИ» логическое «НЕ»

| 
|  
| 
| 
|  Ú Ú 
| 
| 
| ||
n - мерные наборы значений переменных БФ называются кортежами. Например, нулевым значениям функции f на рис.1 соответствуют 4 кортежа входных переменных (001), (011), (100), (101). В геометрической интерпретации кортежи представляют собой точки пространства, мерность которого определяется количеством переменных данной функции, а координаты – значениями переменных. Значения самой функции на соответствующих наборах переменных приписаны вершинам. На рис.2 показана геометрическая интерпретация булевой функции из таблицы истинности рис.1.


 Х2
Х2
1 010 1 110


 0 011 1 111
0 011 1 111


 Х1
Х1
1 000 0 100


 Х3 0 001 0 101
Х3 0 001 0 101
Рис. 2. Булева функция f от трех переменных в геометрической интерпретации.
1.2.ДОКАЗАТЕЛЬСТВА РАВЕНСТВА БУЛЕВЫХ ФУНКЦИЙ.
Существует два способа доказательства равенства булевых функций:
1. С помощью таблиц истинности;
2. С помощью основных законов алгебры логики.
Таблица истинности является основным методом при доказательстве тождеств.
Назовем тождеством такое равенство, которое справедливо для любых значений переменных. Так, выражение  является равенством только на наборе x 1=0 и x 2=0. На всех остальных наборах равенство не справедливо. Т. е.
является равенством только на наборе x 1=0 и x 2=0. На всех остальных наборах равенство не справедливо. Т. е. 
 не тождество.
не тождество.
Пример 1. Доказать, что  является тождеством.
является тождеством.
Доказательство. Строим таблицу истинности для 2-х переменных и вычисляем значения для правой и левой частей равенства.

| 
| 
| 
| 
| 
|
| 0 0 0 1 1 0 1 1 |
Т. к. результаты вычислений правой и левой частей выражения одинаковы на всех наборах, то данное равенство является тождеством.
1.3.ОСНОВНЫЕ ЗАКОНЫБУЛЕВОЙ АЛГЕБРЫ
В булевой алгебре существует система тождеств, применяемых для преобразований выражений или для вычисления их значений без использования таблиц истинности. Эти тождества называются основными законами булевой алгебры. Перечислим их:
Закон идемпотентности: 
Закон коммутативности: 
Закон ассоциативности:

Закон дистрибутивности: 
Закон склеивания: 
Закон поглощения: 
Закон де Моргана: 
Закон двойного отрицания: 
Законы для действий с константами:  ;
;

Видно, что часть законов аналогична законам линейной алгебры как, например, дистрибутивность для умножения  и невозможна в линейной алгебре –
и невозможна в линейной алгебре –  – дистрибутивность для сложения.
– дистрибутивность для сложения.
Пример 2. Сократить выражение, используя основные законы алгебры логики

В решении использованы закон де Моргана и закон поглощения. При решении задач на преобразование выражений необходимо учитывать порядок действий, который определяется приоритетом функции и может быть изменен использованием скобок.
1.4.О КОЛИЧЕСТВЕ ДВОИЧНЫХ НАБОРОВ БУЛЕВЫХ ФУНКЦИЙ И КОЛИЧЕСТВЕ БУЛЕВЫХ. ФУНКЦИЙ ОТ N-ПЕРЕМЕННЫХ
В таблице на рис.1 трехмерные наборы расположены в порядке возрастания их номеров в двоичном коде начиная с номера ноль и заканчивая номером семь в десятичной системе счисления - 0(10) = 000(2) 7(10) = 111(2). Начальный набор, состоящий только из нулей, в таблицах функций принято называть нулевым набором, а последний, состоящий только из единиц - единичным. Двоичный набор полностью определяется своим номером и своей размерностью.
Пример 3. «Значение функции от 5 переменных равно 1 на 4-м наборе» означает, что f (0,0,0,1,1)=1,а не f (1,1)=1 или f (0,1,1)=1, хотя все двоичные наборы (00011), (11) и (011) одинаково равны десятичной тройке.
Наборы n -ой размерности пронумеруем целыми числами от 0 до 2 n -1, откуда следует зависимость: для функции от n переменных имеется точно 2n двоичных n-мерных наборов (n=1, 2,…).
Подсчитаем число различных булевых функций от n переменных. В качестве примера рассмотрим сначала функции от двух переменных и построим таблицу всех возможных функций (табл. 4).
Таблица 4
| x1x2 | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 |
Принцип построения каждой новой функции такой же, как и при построении каждого нового набора – десятичный номер набора или функции соответствует их двоичным кодам. Следовательно, количество функций, как и наборов, определяется количеством двоичных разрядов как 2 k,
где k =2 n – для определения количества функций,
k = n – для определения количества исходных наборов функций (n -количество переменных функции).
Отсюда следующая зависимость: для функции от n
переменных имеется точно  различных булевых функций (n=1,2,…)
различных булевых функций (n=1,2,…)
Порядок действий определяется приоритетом функций, и может быть изменен с помощью скобок.
Функции в порядке убывания приоритета: –, &, Ú.
В приведенных ниже примерах а и б сносками с номерами показан порядок действий.



 2 3 4 2 1 4 3 6 5
2 3 4 2 1 4 3 6 5





 а)
а)  ; б)
; б) 
Задача 1. Вычислить значения выражений а и б на всех наборах переменных.
 x1x2x3 x1x2x3
| a) 1 | а) 2 | a) 3 | a) 4 | б) 1 | б) 2 | б) 3 | б) 4 | б) 5 |  б) 6 б) 6
|
| 0 0 0 | ||||||||||
| 0 0 1 | ||||||||||
| 0 1 0 | ||||||||||
| 0 1 1 | ||||||||||
| 1 0 0 | ||||||||||
| 1 0 1 | ||||||||||
| 1 1 0 | ||||||||||
| 1 1 1 |
СИСТЕМЫИ БАЗИСЫБУЛЕВЫХ ФУНКЦИЙ
Количество различных булевых функций зависит от количества переменных и значности логики. В двузначной логике это количество равно  , где n – число переменных булевых функций.
, где n – число переменных булевых функций.
В таблице 4 приведены функции от двух переменных. Перечислим их:
 – константа «0»;
– константа «0»;
 – конъюнкция;
– конъюнкция;
 – левая коимпликация;
– левая коимпликация;
 – сохраняющая x 1;
– сохраняющая x 1;
 – правая коимпликация;
– правая коимпликация;
 – функция, сохраняющая x 2;
– функция, сохраняющая x 2;
 – сложение по модулю 2, или функция нечетности, или неэквивалентности;
– сложение по модулю 2, или функция нечетности, или неэквивалентности;
 – дизъюнкция;
– дизъюнкция;
 – функция Вебба;
– функция Вебба;
 – эквивалентность, или функция четности, или равнозначности;
– эквивалентность, или функция четности, или равнозначности;
 – отрицание, инверсия;
– отрицание, инверсия;
 – правая импликация («из x 2 следует x 1», «если x 2, то x 1»);
– правая импликация («из x 2 следует x 1», «если x 2, то x 1»);
 – отрицание, инверсия;
– отрицание, инверсия;
 – левая импликация;
– левая импликация;
 – функция Шеффера;
– функция Шеффера;
 – константа «1».
– константа «1».
Различных булевых функций от двух переменных – 16, от трех переменных – 256 и т.д., но все ли они необходимы при составлении логических выражений. Возникает вопрос, можно ли использовать ограниченные совокупности булевых функций для представления логического высказывания любой сложности. Из каких функций эти совокупности должны состоять? Скажем, что такие совокупности функций называются системами и базисами булевых функций.
Определение. Системой булевых функций называется такая их совокупность, с помощью которой можно построить любое логическое выражение, а возможность строить любые логические выражения называется полнотой системы.
Базисом булевых функций называется такая система булевых функций, из которой невозможно удалить ни одной функции без потери этой системой полноты.
Для решения вопроса о том, какая совокупность функций является системой или базисом булевых функций применяется критерий полноты.
1.6. КРИТЕРИЙ ПОЛНОТЫСИСТЕМ БУЛЕВЫХ ФУНКЦИЙ ПОСТА-ЯБЛОНСКОГО
Система S булевых функций fi является полной тогда и только тогда, когда среди булевых функций  найдется
найдется
– хотя бы одна  , не сохраняющая 0 (не принадлежащая классу К0);
, не сохраняющая 0 (не принадлежащая классу К0);
– хотя бы одна  , не сохраняющая 1 (не принадлежащая классу К1);
, не сохраняющая 1 (не принадлежащая классу К1);
– хотя бы одна  нелинейная (не принадлежащая классу КЛ);
нелинейная (не принадлежащая классу КЛ);
– хотя бы одна  несамодвойственная (не принадлежащая классу КС);
несамодвойственная (не принадлежащая классу КС);
– хотя бы одна  немонотонная (не принадлежащая классу КМ);
немонотонная (не принадлежащая классу КМ);
Приведем определения свойств булевых функций, принадлежащих пяти вышеперечисленным классам булевых функций.
 Классом К0 булевых функций называется множество
Классом К0 булевых функций называется множество  таких, что
таких, что  .
.

В двузначной логике P2 таких функций ровно половина, т.е.  , так же, как и принадлежащих К1.
, так же, как и принадлежащих К1.
Классом К1 булевых функций называют множество  таких, что
таких, что  .
.

Классом КЛ линейных булевых функций называют множество функций  таких, что
таких, что  ,
,
где  – коэффициенты, определяемые для
– коэффициенты, определяемые для  ,
,
 – сумма по модулю 2,
– сумма по модулю 2,
 – полином Жегалкина.
– полином Жегалкина.
Классом КС самодвойственных булевых функций, называются такие  , для которых на противоположных наборах переменных
, для которых на противоположных наборах переменных  и
и  значения функций также противоположны
значения функций также противоположны 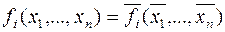 .
.
Число самодвойственных функций от n -переменных  (n–1, так как противоположных пар входных наборов в 2 раза меньше, чем
(n–1, так как противоположных пар входных наборов в 2 раза меньше, чем  ).
).
Классом КМ монотонных БФ называется множество таких 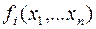 , у которых значения функции на сравниваемых наборах
, у которых значения функции на сравниваемых наборах  при том, что сравниваемые наборы k и l являются склеиваемыми
при том, что сравниваемые наборы k и l являются склеиваемыми
 .
.
Определим, является ли полной система, состоящая из функции  .
.
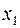
| 
| 
| # |
  0 0
| |||
 1 1
| |||
K0: 
K1: 
KЛ: 
Определим неопределенные коэффициенты, начиная с c 0 на нулевом наборе.


 можно определить на наборе (100), когда полином сокращается до
можно определить на наборе (100), когда полином сокращается до  из-за значений x 2 и x 3, равных 0.
из-за значений x 2 и x 3, равных 0.

Аналогично поступим при определении  и
и  .
.

