Необходимые сведения из теории
Дана система, состоящая из m линейных уравнений и неравенств с n переменными
и линейная функция
Необходимо найти такое решение системы 
, где 
, при котором линейная (целевая) функция L принимает оптимальное (т.е. минимальное или максимальное) значение.
· Если все переменные хi неотрицательны, а система ограничений состоит лишь из одних неравенств, то такая задача называется основной (чаще – стандартной); если система ограничений состоит из одних уравнений, то задача называется канонической. А если ограничения состоят из неравенств и уравнений, то это общая задача линейного программирования.
Как от стандартной задачи линейного программирования перейти к канонической и наоборот? Рассмотрим неравенство 
. В этом неравенстве левая часть меньше правой. Можно подобрать такое число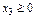 
, которое при добавлении его к левой части, привело бы неравенство к равенству: 
. Если же необходимо перейти от канонической задачи к стандартной, то из уравнения исключают некоторую неотрицательную переменную.
· Оптимальным решением (или оптимальным планом) задачи линейного программирования называется такое решение , которое удовлетворяет системе ограничений и условию неотрицательности (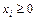
), при котором целевая функция принимает оптимальное (минимальное или максимальное) значение.
Задание.
Составить математическую модель задачи и найти оптимальное решение.
| Вариант | Задача |
| Рацион для питания животных на ферме состоит из двух видов кормов 1 и 2. Один килограмм корма 1 стоит 80 руб. и содержит: 1 ед. жиров, 3 ед. белков, 1 ед. углеводов, 2 ед. нитратов. Один килограмм корма 2 стоит 10 руб. и содержит: 3 ед. жиров, 1 ед. белков, 8 ед. углеводов, 4 ед. нитратов. Составить наиболее дешевый рацион питания, обеспечивающий жиров не менее 6 ед., белков не менее 9 ед., углеводов не менее 8 ед., нитратов не более 16 ед. | |
| В одном грамме малины содержится 14 мг витамина А и 12 мг витамина С; в одном грамме клубники – 7 мг витамина А и 5 мг витамина С. Сколько граммов малины и клубники следует включить в дневной рацион, чтобы в нем оказалось не менее 6 мг витамина А и не менее 75 витамина С при минимальных затратах, если один килограмм малины стоит 25 руб., а 1 килограмм клубники – 40 руб. | |
| В швейном цехе имеется 84 м. ткани первого вида и 58 м. ткани второго вида. На пошив одного халата требуется 4 м. ткани, первого вида и 0.5 м. ткани второго вида. На одну куртку – 3 м. и 1 м. ткани каждого вида соответственно. Сколько следует изготовить халатов и курток для получения наибольшей прибыли от реализации продукции, если халат стоит 160 руб., а куртка – 300 руб. Известно, что халатов можно изготовить не более 15, а курток – не более 20. | |
| Небольшая фирма производит два вида продукции: столы и стулья. Для изготовления одного стула требуется 3 фута древесины, а для изготовления одного стола – 7 футов. На изготовление одного стула уходит 2 часа рабочего времени, а на изготовление стола – 8 часов. Каждый стол приносит 1 доллар прибыли, а каждый стол – 3 доллара. Сколько стульев и сколько столов должна изготовить фирма, если она располагает 420 футами древесины и 400 часами рабочего времени хочет получить максимальную прибыль? | |
| Для откорма животных употребляется два вида корма: 1 и 2. К каждом килограмме корма 1 содержится 5 ед. питательного вещества А и 2.5 ед. питательного вещества В, а в каждом килограмме корма 2 содержится 3 ед. питательного вещества А и 3 ед. питательного вещества В. Экспериментальным путём было установлено, что откорм животных выгоден, когда каждое животное будет получать в дневном рационе не менее 30 ед. питательного вещества А и не менее 22.5 ед. вещества В. Известно, что стоимость 1 кг корма 1 и 1-го кг корма 2 равна каждая одной денежной единице. Какой должен быть ежедневный расход корма каждого вида, чтобы затраты на корм были минимальными и были соблюдены условия питания. | |
| Для сохранения здоровья человек должен потреблять в сутки питательных веществ В1 не менее 4 ед., В2 – не менее 6 ед., В3 – 9 ед., В4 – 6 ед. Имеется два вида пищи: 1 и 2. В 1 кг пищи 1 содержится питательных веществ: В1 – 2, В2 – 0, В3 – 1, В4 – 3. В одном кг пищи 2 содержится: В1 – 1, В2 – 3, В3 – 3, В4 – 2. 1 кг пищи 1 стоит 30 руб., 1 кг пищи 2 стоит 20 руб. Требуется так организовать питание, чтобы стоимость его была наименьшей, а организм получал бы суточную норму, указанную выше. | |
| В одном грамме вишни содержится 3 мг витамина А и 150 мг витамина С; в одном грамме абрикосов – 24 мг витамина А и 75 мг витамина С. Сколько граммов вишни и сколько абрикосов следует включить в дневной рацион, чтобы в нем оказалось не менее 6 мг витамина А и не менее 75 витамина С при минимальных затратах, если один кг вишни стоит 125 руб, а 1 кг абрикосов – 90 руб. | |
| Кондитерская фабрика для производства трех видов карамели А, В и С использует три вида основного сырья: сахарный песок, патоку и фруктовое пюре. На производство одной тонны карамели вида А необходимо 0.8 тонны сахарного песка и 0.4 тонны патоки; на производство карамели вида В необходимо 0.5 тонны сахарного песка, 0.4 тонны патоки и 0.1 тонну фруктового пюре; а на производство тонны карамели вида С необходимо 0.6 тонны сахарного песка, 0.3 тонны патоки и 0.1 тонну фруктового пюре. Прибыль от реализации одной тонны карамели каждого вида – 108 руб., 112 руб. и 126 руб. соответственно. Найти план производства карамели, обеспечивающий максимальную прибыль от ее реализации, используя не более 800 тонн сахарного песка, не более 600 тонн патоки и не более 120 тонн фруктового пюре. | |
| Швейный цех занимается пошивом халатов. На пошив одного халата требуется 3.5 м ткани вида А и 1 м ткани вида В, а на одно платье – 4 м ткани вида А и 0.5 м ткани вида В. Сколько следует изготовить халатов и платьев для получения наибольшей прибыли от реализации продукции, если халат стоит 260 руб., а платье – 330 руб., при этом следует использовать не более 120 м ткани вида А и 50 м ткани вида В | |
| Для производства изделий вида 1 предприятию требуется 15 м3 древесины и 4 м3 металла, а для производства изделий вида 2 требуется 4 м3 древесины и 11 м3 металла. Прибыль от продажи одного изделия каждого вида равна 800 руб. и 900 руб. соответственно. Составить такой план производства продукции, при котором прибыль была максимальной, если использовать при этом не менее 350 м3 древесины и не менее 440 м3 металла. | |
| Для производства трех видов продукции требуется два вида сырья, которое имеется на складе в количестве не менее 62 и не менее 23 единицы соответственно. Для производства единицы продукции первого вида требуется 10 единиц сырья вида I и 3 единицы сырья вида II; для продукции второго вида 7 и 5 единиц сырья каждого вида, а для продукции третьего вида – 5 и 7 единиц сырья. Составить план производства продукции, при котором прибыль была бы максимальной, если известно, что единица продукции первого вида приносит прибыль 300 руб., второго – 290 руб., а третьего – 280 руб. | |
| Имеются четыре продукта, содержащие полезные вещества трех видов. Цена каждого из продуктов равна соответственно 20, 20, 30 и 40 руб. В первом продукте содержатся 3 единицы вещества А, 2 единицы вещества В и 2 единицы вещества С. Во втором продукте содержится 2 единицы вещества А, 2 единицы вещества В и 1 единица вещества С. В третьем – 1, 3 и 3 единицы веществ А, В и С соответственно, а в четвертом – 1, 3 и 2 единицы веществ А, В и С. Необходимо составить смесь, содержащую не менее 11 единиц вещества А, не менее 9 единиц вещества В и не менее 5 единиц вещества С так, чтобы стоимость смеси была минимальной. | |
| Для приготовления смеси использовали три продукта, содержащие три вещества: А, В и С. В первом продукте имеется 5г вещества А, 8г вещества В и 12г вещества С. Во втором продукте содержатся: вещество А – 2г, вещество В – 4г, вещество С – 9г; в третьем продукте – 6г, 9г и 1г веществ А, В и С соответственно. Необходимо составить смесь так, чтобы в нее входило не менее 34г вещества А, не менее 42г вещества В и не менее 78г вещества С, и ее стоимость была минимальной, если известна стоимость каждого из продуктов: 250 руб., 200 руб. и 210 руб. соответственно. | |
| Рацион для питания животных на ферме состоит из трех видов кормов. Один килограмм первого корма стоит 70 руб. и содержит: 0,5 ед. жиров, 0,4 ед. белков и 0,8 ед. углеводов. Один килограмм второго корма стоит 75 руб. и содержит 0,7 ед. жиров, 0,3 ед. белков и 0,6 ед. углеводов. Один килограмм третьего корма стоит 64 руб. и содержит 0,6 ед. жиров, 0,9 ед. белков и 0,2 ед. углеводов.Составить наиболее дешевый рацион питания, обеспечивающий жиров не менее 12 ед., белков не менее 10 ед. и углеводов не менее 9 ед. | |
| Известно, что откорм животных экономически выгоден при условии, когда каждое животное получает в дневном рационе не менее 12 единиц питательного вещества А, не менее 15 единиц вещества В и не менее 10 единиц вещества С. Для откорма животных используется три вида кормов. В корме первого вида содержится 1.2 единицы вещества А, 2.5 единицы вещества В и 1 единица вещества С. В корме второго вида содержится 1.3 единиц вещества А, 2.9 единицы вещества В и 1 единица вещества С. В корме третьего вида содержится 1.1 единиц вещества А, 2.7 единицы вещества В и 1.1 единиц вещества С. Цена корма первого вида равна 70 руб. за 1 кг, корма второго вида 73 руб. за 1 кг, а третьего вида – 68 руб. за 1 кг. Какое количество корма каждого вида необходимо расходовать, чтобы затраты на него были минимальны. |