Несложных мехатронных устройств и систем
Преподаватель: Ванин Владимир Агафонович
Практическая работа № 2.
Построение амплитудно-частотной, фазово-частотной и
Амплитудной фазово-частотной характеристик апериодического звена САУ
Цель работы:
Ознакомиться с режимами работы объекта управления и его динамическими
Характеристиками.
Научится рассчитывать и графически представлять динамические
Характеристики типового звена САУ.
Порядок выполнения работы:
Ознакомиться с описанием «Практической работы».
Для исследования САУ используется метод математического моделирования. При этом объект рассматривается как простой преобразователь входного сигнала в выходной без учета физико-химической сущности процесса, протекающего в нем, т.е. целью исследования объекта управления (ОУ) является формирование его математической модели — уравнения взаимосвязи выходного сигнала объекта (регулируемого параметра) с входным сигналом.
Объект управления может работать в 2-х режимах: статическом и динамическом.
При статическом режиме приток энергии или вещества в объект равен оттоку и объект находится в состоянии равновесия.
При динамическом режиме нарушено равновесие между притоком и оттоком энергии или вещества.
Математическая модель ОУ или уравнение математической взаимосвязи его выходного и входного сигналов в динамическом режиме работы называется динамической характеристикой.
Поскольку в динамическом режиме работы выходной и входной сигналы ОУ изменяются во времени или пространстве, то его динамическая характеристика, как правило, описывается дифференциальным уравнением. В настоящее время дифференциальные уравнения являются основным инструментом при математическом описании всего, что изменяется во времени и пространстве. Однако, большинство дифференциальных уравнений не имеет общего решения, а частные решения требуют много вычислений. Если при исследовании не учитывать физико-химическую сущность технологических процессов, протекающих в ОУ (т.е. рассматривать его как «черный ящик»), оказывается, что различные по своему объему, конфигурации и назначению ОУ в динамическом режиме описываются одними и теми же типами уравнений взаимосвязи выходного и входного сигналов.
В ТАУ (теория автоматического управления) удачно подобраны всего 6 типов уравнений взаимосвязи выходного и входного сигналов объектов (или элементов) САУ, которые названы типовыми динамическими звеньями (ТДЗ) и составляют математический аппарат, используемый при исследовании объектов в целях получения математических моделей.
Методика применения ТДЗ заключается в следующем. На действующий ОУ (то, что объект уже должен работать, является недостатком данного метода) по входному каналу подается одно из 3-х типовых возмущающих воздействий (рис. 1):
1) единичный скачок (рис. 1, а);
2) единичный импульс (рис. 1, б);
3) синусоидальные колебания с различными частотой ώ или периодом Т (рис. 1, в).
На практике чаще всего используют возмущающее воздействие в виде единичного скачка. Реакция объекта на это возмущение (график изменения во времени выходного сигнала объекта после подачи его на вход возмущения в виде единичного скачка) называется переходной характеристикой.

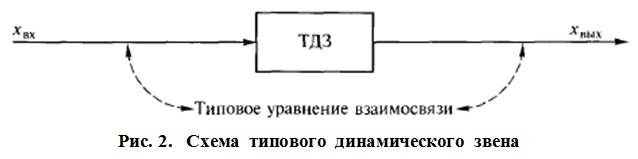
На рис. 2 схематично изображено типовое динамическое звено. Схема ТДЗ похожа на схему исследования управляемого объекта; принципиальное их различие состоит в том, что ОУ — это материальное воплощение технологическою процесса, а ТДЗ — математическая абстракция, за которой нет ничего кроме типового уравнения взаимосвязи его выходного и входного сигналов.
Каждое ТДЗ имеет свою типовую переходную и ряд других типовых характеристик. Полученную на действующем ОУ экспериментальную переходную характеристику сравнивают с набором 6-и переходных характеристик ТДЗ и при совпадении принципа изменения во времени экспериментальной и какой-либо типовой переходной характеристики проводят замену (аппроксимацию) исследуемого ОУ соответствующим ТДЗ.
Таким образом, типовое уравнение взаимосвязи выходного и входного сигналов ТДЗ становится уравнением взаимосвязи соответствующих сигналов объекта, или искомой математической моделью. Коэффициенты, входящие в уравнение ТДЗ, находят по экспериментальной переходной характеристике объекта.
Дифференциальное уравнение, как сказано выше, является неудобной формой математической модели звена или ОУ, так как решение большинства дифференциальных уравнений - это сложная вычислительная процедура. Более удобна математическая модель объекта, записанная в виде передаточной функции.
Передаточной функцией называется преобразованное по Лапласу исходное дифференциальное уравнение, т.е. уравнение, записанное в виде отношения преобразованных по Лапласу выходного и входного сигналов звена (ОУ).
В преобразовании по Лапласу исходное дифференциальное уравнение называется оригиналом, а преобразованное и записанное в операторной форме уравнение — его изображением. Суть преобразования Лапласа заключается в замене функций вещественных переменных Хвых (t) и Хвх (t) на функции комплексных переменных
Хвых (p) и Хвх (p), где р — оператор Лапласа (комплексное число 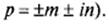
Амплитудной частотной (или амплитудно-частотной) характеристикой (АЧХ) называется зависимость отношения амплитуды выходных колебаний к амплитуде входных колебаний Авых / Авх от частоты колебаний ώ и обозначается А (ώ).
Фазовой частотной ( или фазово-частотной) характеристикой (ФЧХ) з ависимость фазового сдвига φ между выходными и входными колебаниями от частоты ώ и обозначается φ (ώ).
Амплитудной фазово-частотной характеристикой системы (АФЧХ) называется отношение выходной величины системы к входной величине, выраженное в комплексной форме и обозначается W (jώ).

Амплитудно-фазовая частотная характеристика строится на комплексной плоскости и представляет собой годограф частотной передаточной функции при изменении частоты ώ от 0 до ∞. То есть АФЧХ - это траектория, описываемая на комплексной плоскости концом радиуса-вектора, модуль и аргумент которого соответственно равны А (ώ)
и φ (ώ), при изменении частоты ώ от 0 до ∞.
АФЧХ системы не зависит от времени. В этом ее принципиальное отличие от
временной характеристики. Если временная характеристика определяет поведение системы в переходном процессе, то АФЧХ выражает зависимость параметров установившихся выходных колебаний от тех же параметров входных колебаний при различных частотах. Однако, несмотря на то, что АФЧХ отображает только установившиеся процессы в системе, она в полной мере определяет также ее динамические свойства подобно временной характеристике или дифференциальным уравнениям.