В качестве примера применения метода конечных разностей рассмотрим краевую задачу на основе одномерного уравнения теплопроводности. Анализируется теплопередача через плоскую бесконечную пластину или изолированный стержень (рис. 1). На одной границе пластины поддерживается постоянная температура Tл, на другой границе – температура Tп. Начальная температура равна T 0, источники тепловыделения внутри пластины отсутствуют.
Рис. 1. Геометрия задачи
При заданных условиях температура будет изменяться только в направлениях, перпендикулярных границе пластины. Если ось О х направить, как показано на рис. 1, то температура в направлении О у и О z может считаться постоянной. Также предположим, что теплофизические характеристики не зависят от температуры. В связи с этим дифференциальное уравнение (1) преобразуется к виду:
 (1)
(1)
Начальные и граничные условия запишутся следующим образом:
 (2)
(2)
Для того чтобы дать полное математическое описание рассматриваемой задачи, необходимо еще задать физические условия однозначности. Если пластина изготовлена из стали, то λ = 46 Вт/(м⋅ºC), ρ = 7800 кг/м3, с = 460 Дж/(кг⋅ºC). Эту задачу в полной математической постановке будем решать методом конечных разностей на равномерной сетке.
Блок-схема будет выглядеть следующим образом:
Результаты расчетов по приведенной программе при L = 0,1 м, λ = 46 Вт/(м⋅ºC), ρ = 7800 кг/м3, с = 460 Дж/(кг⋅ºC), Т 0=20 °С, Т л = 300 °С, Т п = 100 °С через 60 секунд процесса нагрева приведены на рис. 4.
Рис. 4. Распределение температуры по толщине пластины в момент
времени t = 60 с
Как отмечалось выше, рассмотренная расчетная схема является неявной, т.е. для определения поля температуры приходится решать
систему линейных алгебраических уравнений. Но помимо предложенной схемы существует также и явная схема. В такой схеме явно определяется поле температуры и не нужно решать систему уравнений для определения прогоночных коэффициентов α i и β i.
Рассмотрим ту же задачу, но уже с использованием явной схемы.
Отличие явной схемы от неявной заключается в аппроксимации
диффузионного слагаемого, а именно, во временном слое на котором
рассматривается неизвестное поле температуры:
 (3)
(3)
Таким образом, в результате аппроксимации частных производных соответствующими конечными разностями получаем следующее соотношения для определения поля температуры:
 (4)
(4)
для определения неизвестного поля температуры никакой системы уравнений для α i и β i решать не требуется.
 (5)
(5)
и аналогичные разностные аналоги краевых условий:
 (6)
(6)
Блок-схема к рассматриваемой задаче (явная схема) имеет вид:
Результаты расчетов по приведенной программе при L = 0,1 м, λ = 46 Вт/(м⋅ºC), ρ = 7800 кг/м3, с = 460 Дж/(кг⋅ºC), Т 0=20 °С, Т 1 = 300 °С, Т 2 = 100 °С через 60 секунд процесса нагрева приведены на рис. 6.
Рис. 6. Распределение температуры по толщине пластины в момент времени t = 60 с (с использованием явной разностной схемы)
Анализируя рисунки 4 и 6, видим, что полученные поля температур идентичны. Покажем, в чем же заключается недостаток явных схем. При использовании данной схемы 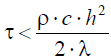 ⋅ Рассмотрим случай
⋅ Рассмотрим случай  как для явной, так и для неявной схемы. С помощью программы, построенной на основе явной схемы, рассчитан только случай N = 50, t = 20.
как для явной, так и для неявной схемы. С помощью программы, построенной на основе явной схемы, рассчитан только случай N = 50, t = 20.
Рис. 7. Распределение температуры по толщине пластины в момент
времени t = 20 с: а – явная схема, б – неявная схема
Рис. 7, а наглядно демонстрирует появление осцилляций при использовании явной схемы, что характеризует её неустойчивость. Неявная же схема напротив дает корректный результат. Рассмотрим одномерное уравнение теплопроводности в цилиндрических координатах.
Определим температурное поле в бесконечном цилиндре радиуса R = 0.1 м через 5, 10, 30 и 60 секунд. Материал цилиндра – кирпич (λ = 0,7 Вт/(м⋅ºC), ρ = 1500 кг/м3, с = 750 Дж/(кг⋅ºC)). Начальная температура 200С
T 0 =. На границе r = R поддерживается постоянная температура Th = 50 0C.
Рис. 8. Геометрия задачи
Математическая постановка задачи будет иметь вид:
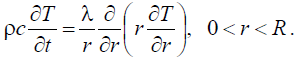 (7)
(7)
Начальные и граничные условия запишутся следующим образом:
 (8)
(8)
Блок-схема к рассматриваемой задаче имеет вид:
В результате были получены следующие распределения температуры
Рис. 9. Распределения температуры по радиусу цилиндра в различные
моменты времени