Рассмотренные выше решения для температурных полей в одномерной и двумерной постановке получены при условии постоянства коэффициента теплопроводности. В действительности коэффициент теплопроводности достаточно часто зависит от температуры. Например, для расчета коэффициента теплопроводности диоксида урана UO2 используется следующая зависимость:
.
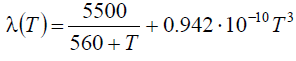Эта формула эмпирическая, коэффициенты размерные T, К; λ, Вт (м ⋅ К). Нелинейное одномерное уравнение теплопроводности в этом случае будет иметь вид:
Для уравнения рассмотрим краевую задачу:
Блок-схема для этой задачи.
Получены следующие распределения температуры:
Рис. 22. Распределения температуры по толщине пластины в различные моменты времени
Рассмотрим чисто неявную схему.
,
где 
Таким образом, в результате аппроксимации частных производных соответствующими конечными разностями получаем следующую систему линейных алгебраических уравнений:
Добавляя к системе конечно-разностные аналоги краевых условий:
получим замкнутую разностную задачу.
Блок-схема к рассматриваемой задаче имеет вид:
Результаты, полученные на основе чисто неявной схемы, полностью совпадают с результатами, полученными по явно-неявной схеме, число итераций при этом не превышает 3.
ОДНОМЕРНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ С
НЕЛИНЕЙНЫМИ ГРАНИЧНЫМИ УСЛОВИЯМИ (ИЗЛУЧЕНИЕ
НА ГРАНИЦЕ)
В качестве примера рассмотрим теплоперенос в бесконечной пластине. Тем самым пренебрегаются два направления переноса тепла, и анализируется одномерное уравнение теплопроводности. На границах области решения будет моделироваться теплообмен за счет конвекции и излучения. Теплоперенос излучением будем рассматривать на основе закона Стефана-Больцмана. Таким образом, сформулированная физическая постановка математически будет выглядеть так:
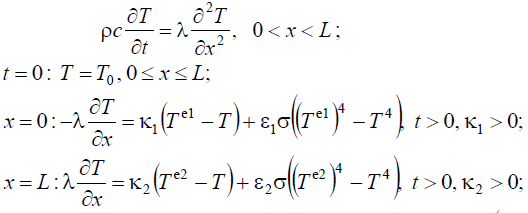
где ε1, ε2 – приведенная степень черноты, σ = 5.669 ⋅10−8 Вт (м2 ⋅ К4) постоянная Стефана-Больцмана.
Блок-схема к рассматриваемой задаче имеет вид:
Получены следующие распределения температуры:
Рис. 23. Распределения температуры по толщине пластины в различные моменты времени
ОДНОМЕРНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ С
ФАЗОВЫМ ПЕРЕХОДОМ НА ГРАНИЦЕ (ИСПАРЕНИЕ
МАТЕРИАЛА)
Рассмотрим процесс теплопроводности в пластине с испарением на двух границах. Математическая постановка задачи:
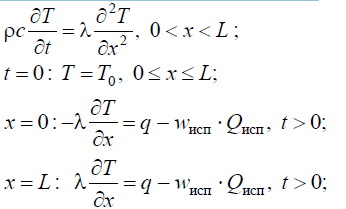
Где 
– скорость испарения, 
– давление насыщенного пара, А – коэффициент аккомодации, P 0 – предэкспонент фазового перехода, Q исп – энергия активации процесса испарения, R = 8.31 Дж (моль ⋅ К) – универсальная газовая постоянная, М – молекулярный вес. В качестве P * рассмотрим атмосферное давление, т.е. P * = P атм.
Блок-схема к рассматриваемой задаче имеет вид:
Получены следующие распределения температуры:
Рис. 24. Распределения температуры по толщине пластины в различные моменты времен.
ЗАКЛЮЧЕНИЕ
В ходе проделанной работы, приобрели основные сведения по методам, алгоритмам и программам решения на ЭВМ основных задач теплопроводности. Были проведены расчеты примеров решения линейных, нелинейных, одномерных, двумерных, нестационарных задач.
СПИСОК ЛИТЕРАТУРЫ
1. Вержбицкий В.М. Основы численных методов. – М.: Высшая
школа, 2002. – 840 c.
2. Самарский А.А. Теория разностных схем. – М.: Наука, 1977. – 656 с.
3. Березин И.С., Жидков Н.П. Методы вычислений. – М.: Наука, 1962.
– Т. 1. – 464 с.
4. Березин И.С., Жидков Н.П. Методы вычислений. – М.: Наука, 1962.
– Т. 2. – 639 с.
5. Калиткин Н.Н. Численные методы. – М.: Наука, 1978. – 512 с.
6. Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. Численные методы.
– М.: Наука, 1987. – 598 с.
7. Волков Е. А. Численные методы. – М.: Наука, 1987. – 248 с.
8. Турчак Л. И. Основы численных методов. – М.: Наука, 1987. – 318 с.
9. Копченова Н. В., Марон И. А. Вычислительная математика в
примерах и задачах. – М.: Наука, 1972. – 367 с.
10. Крылов В. И., Бобков В. В., Монастырный П. И. Вычислительные
методы. – М.: Наука, 1976. – Т. 1. – 302 с.
11. Демидович Б. П., Марон И. А. Основы вычислительной
математики. – М.: Наука, 1966. – 695 с.
12. Петухов Б.С., Генин Л.Г., Ковалев С.А., Соловьев С.Л. Теплообмен
в ядерных энергетических установках. – М.: Изд-во МЭИ, 2003. –
548 с.
13. Лыков А.В. Теория теплопроводности. – М.: Высшая школа, 1967. –
600 с.
14. Лыков А.В. Тепломассообмен: (Справочник). – М.: Энергия, 1978. –
480 с. 15. Самарский А.А., Вабищевич П.Н. Вычислительная теплопередача.
– М.: Едиториал УРСС, 2003. – 782 с.
16. Берковский Б.М., Ноготов Е.Ф. Разностные методы исследования
задач теплообмена. – Минск: Наука и техника, 1976. – 141 с.