Векторные (линейные) пространства
Вектор. Основные понятия
Повторим некоторые понятия, известные из школьного курса геометрии.
Определение. Вектором с началом в точке А и концом в точке В называется направленный отрезок АВ.
Обозначение:  ,
,  .
.
Определение. Вектор, начало и конец которого совпадают, называется нулевым и обозначается  или
или  .
.
Определение. Длиной ненулевого вектора  называется длина отрезка
называется длина отрезка  . Длина вектора обозначается
. Длина вектора обозначается  . Длина нулевого вектора равна нулю.
. Длина нулевого вектора равна нулю.
Определение. Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Обозначение:  ǀǀ
ǀǀ 
Определение. Два ненулевых вектора  и
и  называются сонаправленными, если сонаправлены лучи
называются сонаправленными, если сонаправлены лучи 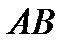 и
и  . Обозначение:
. Обозначение:  Два ненулевых вектора
Два ненулевых вектора  и
и  называются противоположно направленными, если противоположно направлены лучи
называются противоположно направленными, если противоположно направлены лучи 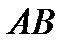 и
и  . Обозначение:
. Обозначение:  .
.
Нулевой вектор считается сонаправленым с любым вектором.
Определение. Векторы называются равными, если они сонаправлены и их длины равны. Обозначение:  .
.
Определение. Два вектора называются противоположными, если они противоположно направлены и их длины равны. Вектор, противоположный вектору  , обозначается
, обозначается  .
.
Пример. Дан параллелограмм  , точки
, точки  и
и  - середины сторон
- середины сторон  и
и 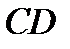 соответственно. Векторы
соответственно. Векторы  и
и  - коллинеарны и, более того, противоположно направлены; векторы
- коллинеарны и, более того, противоположно направлены; векторы  и
и  - коллинеарны и сонаправлены;
- коллинеарны и сонаправлены;  ;
;  .
.
Сложение и вычитание векторов
Определение. Пусть  и
и  - произвольные векторы. Возьмём любую точку
- произвольные векторы. Возьмём любую точку  и отложим от неё вектор
и отложим от неё вектор  , затем от точки
, затем от точки  отложим вектор
отложим вектор  . Вектор
. Вектор  называется суммой векторов
называется суммой векторов  и
и  и обозначается:
и обозначается:  (рис.2).
(рис.2).
Замечания.
1. Можно показать, что вектор  определяется с помощью векторов
определяется с помощью векторов  и
и  однозначно, не зависимо от точки
однозначно, не зависимо от точки  .
.
2. При нахождении суммы двух неколлинеарных векторов приходится строить треугольник  , поэтому указанное здесь правило сложения векторов называется правилом треугольника.
, поэтому указанное здесь правило сложения векторов называется правилом треугольника.
Если слагаемые векторы  и
и  неколлинеарные. То для построения их суммы можно пользоваться другим способом – правилом параллелограмма.
неколлинеарные. То для построения их суммы можно пользоваться другим способом – правилом параллелограмма.
В этом случае от одной точки

откладываем векторы

и

. Затем на этих векторах как на смежных сторонах строиться параллелограмм

. Тогда суммой векторов

и

называется вектор

(рис. 3).
Свойства сложения.
Для произвольных векторов  ,
,  и
и  справедливо следующие равенства.
справедливо следующие равенства.
1.  - свойство коммутативности (переместительный закон).
- свойство коммутативности (переместительный закон).
2.  - свойство ассоциативности (сочетательный закон).
- свойство ассоциативности (сочетательный закон).
3. 
4. 
Наиболее сложным из этих свойств является свойство ассоциативности. Проиллюстрируем его. Для этого от произвольной точки  отложим последовательно векторы
отложим последовательно векторы  ,
, 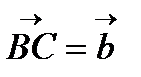 и
и  (рис. 4).
(рис. 4).
Дважды применяя правило треугольника получаем
 .
.
Точно также находим, что  .
.
Сумма трех векторов определяется с помощью сложения двух векторов, а именно:  . Из свойств коммутативности и ассоциативности следует, что в сумме трех векторов скобки можно расставлять произвольным образом, а векторы можно складывать в произвольном порядке. Аналогичным образом определяется сумма числа векторов, большего трёх. Для построения суммы нескольких векторов используется правило многоугольника:
. Из свойств коммутативности и ассоциативности следует, что в сумме трех векторов скобки можно расставлять произвольным образом, а векторы можно складывать в произвольном порядке. Аналогичным образом определяется сумма числа векторов, большего трёх. Для построения суммы нескольких векторов используется правило многоугольника:
Первый вектор суммы откладывается от произвольной точки. Каждый следующий вектор откладывается от конца предыдущего. Суммой является вектор с началом в начале первого слагаемого и концом – в конце последнего слагаемого.
Пример. Пусть даны векторы

. Построим вектор
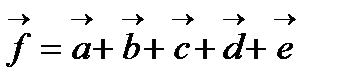
(рис. 5).
Определение. Три вектора называются компланарными, если существует плоскость, которой они параллельны.
Если три вектора  и
и  не компланарны, то для их сложения применяют также правило параллелепипеда. В этом случае векторы
не компланарны, то для их сложения применяют также правило параллелепипеда. В этом случае векторы  и
и  откладывают от одной точки
откладывают от одной точки  , затем на построенных векторах как на смежных ребрах строят параллелепипед. Суммой векторов является вектор, совпадающий с диагональю параллелепипеда, выходящей из точки
, затем на построенных векторах как на смежных ребрах строят параллелепипед. Суммой векторов является вектор, совпадающий с диагональю параллелепипеда, выходящей из точки  .
.
Определение. Разностью векторов  и
и  называется такой вектор
называется такой вектор  , что
, что  . Обозначается:
. Обозначается:  .
.
Из определения следует, что  .
.
Согласно правилу треугольника

(рис.6), поэтому

, откуда получаем правило нахождения разности векторов

и

.
От точки  откладываем векторы
откладываем векторы  и
и  , тогда разность
, тогда разность  - это вектор с началом в конце вычитаемого и концом в конце уменьшаемого.
- это вектор с началом в конце вычитаемого и концом в конце уменьшаемого.
 ,
,  .
. или
или  .
. называется длина отрезка
называется длина отрезка  . Длина вектора обозначается
. Длина вектора обозначается  . Длина нулевого вектора равна нулю.
. Длина нулевого вектора равна нулю. ǀǀ
ǀǀ 
 и
и  называются сонаправленными, если сонаправлены лучи
называются сонаправленными, если сонаправлены лучи 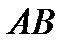 и
и  . Обозначение:
. Обозначение:  Два ненулевых вектора
Два ненулевых вектора  и
и  называются противоположно направленными, если противоположно направлены лучи
называются противоположно направленными, если противоположно направлены лучи 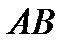 и
и  . Обозначение:
. Обозначение:  .
. .
. , обозначается
, обозначается  .
. , точки
, точки  и
и  - середины сторон
- середины сторон  и
и 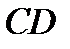 соответственно. Векторы
соответственно. Векторы  и
и  - коллинеарны и, более того, противоположно направлены; векторы
- коллинеарны и, более того, противоположно направлены; векторы  и
и  - коллинеарны и сонаправлены;
- коллинеарны и сонаправлены;  ;
;  .
. и
и  - произвольные векторы. Возьмём любую точку
- произвольные векторы. Возьмём любую точку  и отложим от неё вектор
и отложим от неё вектор  , затем от точки
, затем от точки  отложим вектор
отложим вектор  . Вектор
. Вектор  называется суммой векторов
называется суммой векторов  и
и  и обозначается:
и обозначается:  (рис.2).
(рис.2).





 определяется с помощью векторов
определяется с помощью векторов  и
и  однозначно, не зависимо от точки
однозначно, не зависимо от точки  .
. , поэтому указанное здесь правило сложения векторов называется правилом треугольника.
, поэтому указанное здесь правило сложения векторов называется правилом треугольника. и
и  неколлинеарные. То для построения их суммы можно пользоваться другим способом – правилом параллелограмма.
неколлинеарные. То для построения их суммы можно пользоваться другим способом – правилом параллелограмма.



 откладываем векторы
откладываем векторы  и
и  . Затем на этих векторах как на смежных сторонах строиться параллелограмм
. Затем на этих векторах как на смежных сторонах строиться параллелограмм  . Тогда суммой векторов
. Тогда суммой векторов  и
и  называется вектор
называется вектор  (рис. 3).
(рис. 3).
 ,
,  и
и  справедливо следующие равенства.
справедливо следующие равенства. - свойство коммутативности (переместительный закон).
- свойство коммутативности (переместительный закон). - свойство ассоциативности (сочетательный закон).
- свойство ассоциативности (сочетательный закон).

 отложим последовательно векторы
отложим последовательно векторы  ,
, 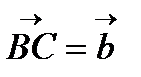 и
и  (рис. 4).
(рис. 4).






 .
. .
. . Из свойств коммутативности и ассоциативности следует, что в сумме трех векторов скобки можно расставлять произвольным образом, а векторы можно складывать в произвольном порядке. Аналогичным образом определяется сумма числа векторов, большего трёх. Для построения суммы нескольких векторов используется правило многоугольника:
. Из свойств коммутативности и ассоциативности следует, что в сумме трех векторов скобки можно расставлять произвольным образом, а векторы можно складывать в произвольном порядке. Аналогичным образом определяется сумма числа векторов, большего трёх. Для построения суммы нескольких векторов используется правило многоугольника:









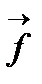
 . Построим вектор
. Построим вектор 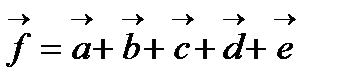 (рис. 5).
(рис. 5).
 и
и  не компланарны, то для их сложения применяют также правило параллелепипеда. В этом случае векторы
не компланарны, то для их сложения применяют также правило параллелепипеда. В этом случае векторы  и
и  откладывают от одной точки
откладывают от одной точки  , затем на построенных векторах как на смежных ребрах строят параллелепипед. Суммой векторов является вектор, совпадающий с диагональю параллелепипеда, выходящей из точки
, затем на построенных векторах как на смежных ребрах строят параллелепипед. Суммой векторов является вектор, совпадающий с диагональю параллелепипеда, выходящей из точки  .
. и
и  называется такой вектор
называется такой вектор  , что
, что  . Обозначается:
. Обозначается:  .
. .
.


 (рис.6), поэтому
(рис.6), поэтому  , откуда получаем правило нахождения разности векторов
, откуда получаем правило нахождения разности векторов  и
и  .
.
 откладываем векторы
откладываем векторы  и
и  , тогда разность
, тогда разность  - это вектор с началом в конце вычитаемого и концом в конце уменьшаемого.
- это вектор с началом в конце вычитаемого и концом в конце уменьшаемого.