Математическое ожидание случайной величины

Схема Бернулли

Предположим, что мы производим некоторое испытание с двумя исходами (например, бросание монеты, когда исходами являются орел или решка, или вытягивание лотерейного билета, когда в результате испытания билет оказывается выигрышным либо проигрышным). Один исход данного испытания (имеющий вероятность p) будем считать успехом и обозначать единицей. Второй исход (имеющий вероятность 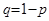) будем считать неудачей и обозначать нулем. Таким образом, совокупность исходов данного испытания мы отождествили с двуточечным множеством .

Повторим теперь это испытание независимым образом n раз. Результатом этого n -кратного эксперимента будут последовательности вида 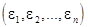, где каждое число () равно нулю либо единице. Например, если 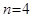и мы получили последовательность , то это означает, что при первом и четвертом испытаниях нас постигла неудача, а второе и третье испытания были успешными. Ясно, что в качестве пространства элементарных событий следует взять множество W, состоящее из всевозможных цепочек вида 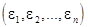, где каждое число () равно нулю либо единице. В качестве s-алгебры F выберем совокупность всех подмножеств множества W.

Остановимся более подробно на определении вероятности P. Обозначим через (соответственно ) событие, состоящее в том, что при k -м испытании нас постигает неудача (соотв., при k -м испытании мы имеем успех). Очевидно, . Так как при разных k испытания производятся независимым образом, то математически это должно означать, что любая система событий должна быть независимой в совокупности в смысле определения 6. То есть вероятность события должна определяться формулой:

.

(7)

Но легко видеть, что событие совпадает с элементарным событием 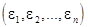, поэтому вероятность каждого элементарного события 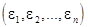должна определяться той же формулой:

.

(8)

Таким образом, мы построили конечное вероятностное пространство (бернуллиевское вероятностное пространство), моделирующее описанный выше n -кратный эксперимент.

Событие 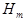состоит в том, что в n испытаниях в схеме Бернулли наступило ровно m успехов.

Теорема 3. Справедлива формула:

,

(9)

где 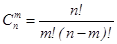– число сочетаний из n элементов по m.

СЛУЧАЙНЫЕ ВЕЛИЧИНЫИ ИХ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ

Случайные величины на конечных вероятностных пространствах

Определение 9. Конечным вероятностным пространством называется такое вероятностное пространство (см. определение 4), у которого пространство элементарных событий W состоит из конечного числа элементов, а s-алгебра F представляет собой совокупность всех подмножеств множества W.

Определение 10. Пусть дано конечное вероятностное пространство . Числовая функция , определенная на пространстве элементарных событий W, называется случайной величиной (с.в.) на .

Для обозначения случайных величин мы, в основном, применяем большие латинские буквы 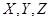и т.д., но иногда будем использовать и малые греческие буквы.

Определение 11. Пусть A – событие из s-алгебры F. Индикатором события A называется случайная величина , заданная формулой:

	(10)

Перечислим некоторые легко доказываемые свойства индикаторов:

1) ;

2) ;

3) ;

4) если , то .

Заметим, что определение 11 и записанные свойства индикаторов имеют силу на произвольных вероятностных пространствах (а не только конечных).

Лемма 2 (о представлении с.в. через индикаторы). Пусть – с.в. на конечном вероятностном пространстве и 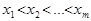– всевозможные значения этой с.в. Пусть событие состоит из всех , для которых , , 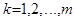то есть . Тогда:

.

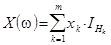(11)

Закон распределения случайной величины

в случае конечного вероятностного пространства

Определение 12. Пусть – с.в. на конечном вероятностном пространстве и 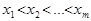– всевозможные значения этой с.в. Законом распределения данной с.в. называется таблица

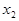
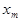
				...			(12)
				...		,

где нижний ряд состоит из чисел 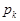, равных вероятностям принятия случайной величиной значений , то есть , причем .

Пример 3. Закон распределения индикатора имеет вид:

		P			.
	

Пример 4. С.в. 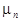, равная числу успехов в серии из n независимых испытаний, в силу формулы (9) имеет следующий закон распределения:

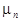
					...	n
	P				...		.

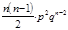
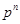
Этот закон распределения называется биномиальным.

Математическое ожидание случайной величины