Определение 15. Дисперсией с.в. 
называется число
 .
| (20) |
Таким образом, дисперсия – это математическое ожидание квадрата отклонения с.в. X от ее математического ожидания.
Свойства дисперсии
1. Справедлива следующая формула для вычисления дисперсии:
 .
| (21) |
2. Для любой с.в. X справедливо неравенство 
. Это неравенство превращается в равенство тогда и только тогда, когда с.в. X постоянна с вероятностью единица.
3. Пусть c – произвольное действительное число. Тогда
 .
| (23) |
4. Если с.в. X и Y независимы (см. определение 14), то
 .
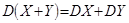| (24) |
Лемма 4. Если с.в. X и Y независимы, а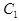 
и 
– действительные числа, то с.в. 
и 
также независимы.
Обобщение свойства 4. Если случайные величины 
попарно независимы, то справедлива формула:
 .
| (25) |
Пример 6 (продолжение примеров 4 и 5). Вычислим дисперсия с.в., распределенной по биномиальному распределению 
. Воспользуемся равенством (15) и формулой (25), получаем, что 
.
Случайные величины на счетном вероятностном пространстве
Определение 16. Счетным вероятностным пространством называется такое вероятностное пространство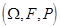 
(см. определение 4), у которого элементы W можно занумеровать целыми неотрицательными числами (то есть 
представляет собой некоторую последовательность), а s-алгебра F представляет собой совокупность всех подмножеств множества W.
С.в. на счетном вероятностном пространстве определяется точно так же, как с.в. на конечном вероятностном пространстве (см. определение 10).
Определение 17. Пусть 
– с.в. на счетном вероятностном пространстве 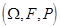и 
– всевозможные различные значения этой с.в. Законом распределения данной с.в. называется таблица с бесконечным числом столбцов:
|
|
| 
| 
| ... | 
| ... | ||||
| 
| 
| ... | 
| ... | , |
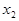
где нижний ряд состоит из чисел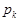 
, равных вероятностям принятия случайной величиной значений 
, то есть 
.
Пример 7
| X | ... | m | ... | ||||
| P | q |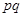 
| 
| ... | 
| ... | (26) |
Закон распределения (26) принято называть геометрическим распределением.
| |
Пример 8. На некотором счетном вероятностном пространстве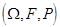 
рассмотрим с.в. X, принимающую значения 0,1,2,..., m,... с вероятностями
,
где число 
. Из теории рядов хорошо известно, что 
. Поэтому
.
Закон распределения с.в. X выражается таблицей:
| X | ... | m | ... | |||||
| P | 
| 
| 
| ... | 
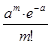
| ... | (27) |
Такой закон распределения называется пуассоновским (с параметром a).
Определение 18. Математическим ожиданием с.в. X на счетном вероятностном пространстве 
называется число:
 .
| (28) |
Дисперсия с.в. X на счетном вероятностном пространстве 
может быть записана в виде ряда с положительными членами:
 .
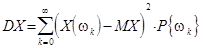| (29) |
Пример 9 (продолжение примера 7). Можно доказать следующие формулы для математического ожидания и дисперсии с.в. X, введенной в примере 6:
 ,
| (30) |
 .
| (31) |
Пример 10 (продолжение примера 8). Вычислим математическое ожидание и дисперсию с.в. X, обладающей пуассоновским законом распределения (см. таблицу (27)) с параметром a. Применяя формулу (28) и (29), получаем следующие соотношения:
 .
| (32) |
Определение 19. Функцией распределения случайной величины 
называется функция 
с областью определения R, задающаяся формулой:
 .
| (33) |
Формулу (33) часто записывают в более лаконичном виде:
.
Свойства функции распределения
|
|
1. 
для всех 
.
2. Функция монотонно возрастает, то есть 
.
3. 
.
4. Функция непрерывна слева, то есть для любого 
.
Ввиду свойств 1–4 функции распределения, примерный вид ее графика таков:
Теорема 7. Пусть функция , определенная на всей действительной прямой, удовлетворяет условиям 1-4 функции распределения. Тогда существует вероятностное пространство и на нем случайная величина X, чья функция распределения совпадает с 
.
Пример 11. Вычислим функцию распределения индикатора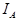 
(определение 11 остается действующим и в случае произвольного вероятностного пространства), если 
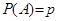. Имеем:
График функции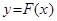 
имеет вид:
Он представляет собой так называемую кусочно-постоянную функцию с двумя скачками. Первый скачок график испытывает в точке 
, причем величина скачка равна 
, то есть вероятности принятия индикатором 
значения 0. Второй скачок график испытывает в точке 
, причем величина скачка равна p, то есть вероятности принятия индикатором значения 1. Теперь совершенно ясно, как с помощью этой функции распределения составить закон распределения (таблицу) из примера 17 и наоборот.
Определение 21. Если с вероятностью 1 с.в. X принимает конечное или счетное (записывающееся в последовательность) число значений, то такая случайная величина называется дискретной.
Все случайные величины, определенные на конечных и счетных вероятностных пространствах являются дискретными.