Бруса при растяжении и сжатии

Тема 2.2. Растяжение и сжатие.

Продольные и поперечные деформации.

Закон Гука

Иметь представление о продольных и поперечных деформациях и их связи.

Знать закон Гука, зависимости и формулы для расчета на­пряжений и перемещений.

Уметь проводить расчеты на прочность и жесткость ста­тически определимых брусьев при растяжении и сжатии.

Деформации при растяжении и сжатии

Рассмотрим деформацию бруса под действием продольной силы F (рис. 21.1).

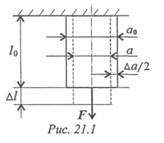Начальные размеры бруса: I 0— на­чальная длина, a0— начальная ширина.

Брус удлиняется на величину Δ l; Δ 1 — абсолютное удлинение. При растя­жении поперечные размеры уменьшают­ся, Δ а— абсолютное сужение; Δ 1 > 0; Δ a<0.

При сжатии выполняется соотноше­ние Δ 1 < 0; Δ а > 0.

В сопротивлении материалов принято рассчитывать деформации в относи­тельных единицах:

Между продольной и поперечной деформациями существует за­висимость

где μ — коэффициент поперечной деформации, или коэффициент Пуассона, —характеристика пластичности материала.

 

 

Тема 2.2. Растяжение и сжатие 183

Закон Гука

В пределах упругих деформаций деформации прямо пропорцио­нальны нагрузке:

где F — действующая нагрузка; к — коэффициент. В современной форме:

Получим зависимость σ = Еε, где Е — модуль упругости, ха­рактеризует жесткость материала.

В пределах упругости нормальные напряжения пропорциональ­ны относительному удлинению.

Значение Е для сталей в пределах (2: 2,1) • 10⁵МПа.

При прочих равных условиях, чем жестче материал, тем меньше он деформируется:

Формулы для расчета перемещений поперечных сечений

бруса при растяжении и сжатии

Используем известные формулы.

Закон Гука σ = Еε.

Откуда

Относительное удлинение

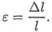
В результате получим зависимость между нагрузкой, размера­ми бруса и возникающей деформацией:

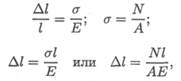
где Δ1 — абсолютное удлинение, мм;

σ — нормальное напряжение, МПа;

184 Лекция 21

I — начальная длина, мм;

Е — модуль упругости материала, МПа;

N — продольная сила, Н;

А — площадь поперечного сечения, мм²;

Произведение АЕ называют жесткостью сечения.

Выводы

1. Абсолютное удлинение бруса прямо пропорционально вели­чине продольной силы в сечении, длине бруса и обратно пропорцио­нально площади поперечного сечения и модулю упругости.

2. Связь между продольной и поперечной деформациями зависит от свойств материала, связь определяется коэффициентом Пуассо­на, называемом коэффициентом поперечной деформации.

Коэффициент Пуассона: у стали μ от 0,25 до 0,3; у пробки μ = 0; у резины μ = 0,5.

3. Поперечные деформации меньше продольных и редко влияют
на работоспособность детали; при необходимости поперечная деформация рассчитывается через продольную.

где Δа — поперечное сужение, мм; а 0— начальный поперечный размер, мм.

3. Закон Гука выполняется в зоне упругих деформаций, которая
определяется при испытаниях на растяжение по диаграмме растя­жения (рис. 21.2).

При работе пластические де­формации не должны возникать, упругие деформации малы по сравнению с геометрическими размерами тела. Основные расче­ты в сопротивлении материалов проводятся в зоне упругих деформаций, где действует закон Гука.

На диаграмме (рис. 21.2) закон Гука действует от точки 0 до точки 1.

Тема 2.2. Растяжение и сжатие 185

5. Определение деформации бруса под нагрузкой и сравнение ее с допускаемой (не нарушающей работоспособности бруса) называют расчетом на жесткость.

Примеры решения задач

Дана схема нагружения и размеры бруса до деформации (рис. 21.3). Брус защемлен, определить перемещение свободного кон­ца.

Решение

1. Брус ступенчатый, по­ этому следует построить эпюры
продольных сил и нормальных напряжений.

Делим брус на участки на­гружения, определяем продоль­ные силы, строим эпюру про­дольных сил.

2. Определяем величины нормальных напряжений по се­чениям с учетом изменений площади поперечного сечения.

Строим эпюру нормальных напряжений.

3. На каждом участке определяем абсолютное удлинение.
Результаты алгебраически суммируем.

Примечание. Бал­ка защемлена, в заделке возника­ет неизвестная реакция в опоре, поэтому расчет начинаем со сво­бодного конца (справа).

1. Два участка нагружения: участок 1: N 1 = +25 кН; растянут;

 

186 Лекция 21

 

 

Контрольные вопросы и задания

1. Стальной стержень длиной 1,5 м вытянулся под нагрузкой на 3 мм. Чему равно относительное удлинение? Чему равно относи­тельное сужение? (μ = 0,25.)

2. Что характеризует коэффициент поперечной деформации?

3. Сформулируйте закон Гука в современной форме при растя­жении и сжатии.

4. Что характеризует модуль упругости материала? Какова еди­ница измерения модуля упругости?

5. Запишите формулы для определения удлинения бруса. Что характеризует произведение АЕ и как оно называется?

6. Как определяют абсолютное удлинение ступенчатого бруса, нагруженного несколькими силами?

7. Ответьте на вопросы тестового задания.

Тема 2.2. Растяжение и сжатие 187