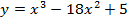Часто бывает рациональнее исследовать функцию на экстремум с помощью второй производной. Рассмотрим сущность этого метода.
Знак первой производной данной функции характеризует возрастание и убывание функции. Точно так же знак второй производной характеризует возрастание и убывание первой производной.
Теперь выясним, как изменяется первая производная в точках экстремума и близких к ним точках с увеличением аргумента. Первая производная при переходе через точку максимума меняет знак с «+» на «-». Иными словами, она от положительных значений переходит через ноль к отрицательным, т. е. убывает, а значит, её производная должна быть отрицательна. Итак, в точке максимума данной функции первая производная равна нулю, а вторая производная отрицательна.
Аналогично можно показать, что в точке минимума функции первая производная равна нулю, а вторая отрицательна.
Отсюда вытекает правило исследования функции на экстремум с помощью второй производной.
1. Найти первую производную 
.
2. Найти критические точки, т.е. точки, в которых 
3. Найти вторую производную 
.
Во вторую производную подставить поочерёдно все критические значения
;
если 
то 
- точка минимума,
если 
то 
- точка максимума,
если 
то следует обратиться к первому правилу.
Вычислить значения функции в точках экстремума и построить схематически график.
П р и м е р. Исследовать функцию на экстремум по второму правилу
Решение. 1. Найдём первую производную 
2. Найдём критические точки
, если 
, 
,
.
3. Найдём вторую производную
.
4. Определим знак второй производной в каждой критической точке.
, значит 
– точка максимума,
, значит 
- точка минимума,
, значит 
5. Вычислим значения функции в точках экстремума.
Точка 
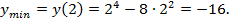. Точка 
.
Точка 
Построим схематически график.
y
- 
x
 | |||
 | |||
Вопросы для самопроверки
1. Что называется точкой максимума функции? Проиллюстрируйте на рисунке.
2. Что называется точкой минимума функции? Покажите, как это выглядит на рисунке.
3. Что такое максимум и минимум функции?
4. Сформулируйте необходимое и достаточное условия существования точек экстремума.
5. Перечислите порядок нахождения точек экстремума по первой производной.
6. Как исследовать функцию на экстремум по второй производной?
УПРАЖНЕНИЯ
1. Исследуйте функции на монотонность и точки экстремума. Постройте график.
1. 
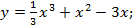
2. 
3. 
4. 
5. 
6. 
;
7. 
8. 
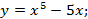
9. 
2. Исследуйте функцию на экстремум по второму правилу.
1. 
2. 
3. 
;
4. 
Задания для самостоятельного решения
1. Исследуйте функцию на монотонность и точки экстремума по первому правилу.
1. 
;
2. 
;
3. 
4. 
;
5. 
;
6. 
7. 
;
8. 
2. Исследуйте функцию на экстремум по второму правилу.
1. 
2.
3. 
;
5. 
.
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИИ
НА МОНОТОННОСТЬ И ЭКСТРЕМУМЫ
1.Исследовать функцию на монотонность и точки экстремума.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
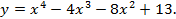
2. Исследовать функцию на экстремум и постройте схематически график:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
;
8. 
9. 
10. 
11. 
12. 
13. 
14. 
3. Исследовать функцию на экстремум по второй производной и построить схе матически график:
1. 
2. 
3. 
4.
5. 