Исследование функции на условный экстремум (для случая двух переменных)
Функция 
имеет условный максимум (минимум) в точке 
, если существует такая окрестность точки , что для всех точек из этой окрестности, удовлетворяющих условию 
, выполняется неравенство 
(или 
).
Задача нахождения условного экстремума сводится к исследованию на обычный экстремум функции Лагранжа
.
Здесь 
называется множителем Лагранжа.
Необходимые условия условного экстремума функции двух переменных выражаются системой трёх уравнений:
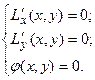(6)
Пусть дана точка и имеем 
- любое из решений этой системы. Составим следующий определитель:
. (7)
Тогда, если 
, то функция имеет в точке условный максимум, если 
, то функция имеет в точке условный минимум.
Пример. Исследовать функцию 
на условный экстремум при условии 
.
Решение. Составим функцию Лагранжа:
.
Получаем:
; 
.
Система (6) принимает вид:
или 
Решим систему методом Крамера.
; 
;
; 
.
Отсюда получаем:
; 
; 
.
Координаты критической (стационарной) точки: 
.
Находим вторые производные функции Лагранжа:
; 
; 
.
Кроме того:
; 
.
Тогда определитель (7):
.
Следовательно, в точке функция имеет условный минимум. Вычислим значения этого минимума:
.
Метод наименьших квадратов
Пусть в некоторой предметной области исследуются показатели X и Y, которые имеют количественное выражение. При этом есть все основания полагать, что показатель Y зависит от показателя X.
Предположим, что после проведения п наблюдений получены следующие числовые данные:
| X | 
| 
| … | 
|
| Y |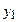 
| 
| … | 
|
Эти табличные данные также можно представить в виде точек 
, 
, …, 
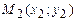и изобразить в декартовой системе координат Оху. Требуется подобрать функцию 
, график которой проходит как можно ближе к точкам 
, 
, …, 
. Такую функцию называют аппроксимирующей (аппроксимация – приближение) или теоретической функцией. При этом разыскиваемая функция должна быть достаточно проста, т.е. легка в обработке, и в то же время должна отражать зависимость адекватно.
Один из методов нахождения таких функций называется методом наименьших квадратов. Его суть заключается в следующем. Пусть некоторая функция 
приближает экспериментальные данные 
, 
, …, 
:
Как оценить точность данного приближения? Вычислим значения функции 
, 
, …, 
и разности (отклонения) 
, 
, …, 
между экспериментальными и функциональными значениями и оценим сумму этих отклонений. При этом, во избежание обнуления сумы из-за наличия отрицательных отклонений, будем возводить их в квадрат: 
, после чего будем искать такую функцию 
, чтобы сумма квадратов отклонений 
была как можно меньше.
Как отмечалось выше, подбираемая функция должна быть достаточно проста. Но таких функций существует немало: линейная, гиперболическая, экспоненциальная, логарифмическая, квадратичная и т.д. Какой класс функций выбрать для исследования? Проще всего изобразить точки 
, , …, на чертеже и проанализировать их расположение. Если они имеют тенденцию располагаться по прямой, то следует искать уравнение прямой 
с оптимальными значениями a и b. Иными словами, задача состоит в нахождении таких коэффициентов a и b, чтобы сумма квадратов отклонений
была наименьшей.
Если же точки расположены, например, по гиперболе, то заведомо понятно, что линейная функция будет давать плохое приближение. В этом случае ищем наиболее «выгодные» коэффициенты a и b для уравнения гиперболы 
. То есть те, которые дают минимальную сумму квадратов
.
Обратите внимание, что в обоих случаях речь идёт о функции двух переменных, аргументами которой являются параметры разыскиваемых зависимостей:
или 
.
И по существу нам требуется решить стандартную задачу – найти минимум функции двух переменных. Для этого сначала вычисляют частные производные 1-го порядка.
Согласно правилу линейности дифференцировать можно прямо под значком суммы:
Составим стандартную систему:
Сокращаем каждое уравнение на «2» и разделяем суммы:
Перепишем систему в более удобном виде:
Теперь приступаем к решению задачи. Координаты точек 
, 
, …, нам известны. Суммы 
, 
, 
, 
находим из решения системы двух линейных уравнений с двумя неизвестными(a и b). Систему решаем, например, методом Крамера, в результате чего получаем стационарную точку 
. Проверяя достаточное условие экстремума, можно убедиться, что в данной точке функция 
достигает именно минимума.
Делаем окончательный вывод: функция 
наилучшим образом приближает экспериментальные точки , , …, , а её график проходит максимально близко к этим точкам.
Источник материала данного пункта:
https://www.mathprofi.ru/metod_naimenshih_kvadratov.html