МАТЕМАТИКА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ
для студентов заочного отделения
(бакалавриат, направления 15.03.02«Технологические машины и оборудование»)
Составители:
А. П. Ильин
Ижевск 2018
ЛИТЕРАТУРА
Письменный Д.Т. Конспект лекций по высшей математике. – М.: Айрис пресс, 2002, ч. 1, 2.
Лунгу К.Н. Сборник задач по высшей математике. – М.: Айрис пресс, 2004, 1,2 курс.
Натансон И.П. Краткий курс высшей математики. – М.: Лань, 2003.
ТАБЛИЦЫВАРИАНТОВ
Студент выполняет вариант контрольной работы, совпадающий с номером в списке группы.
ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ КОНТРОЛЬНЫХ РАБОТ
1. Привести уравнения данных гармонических колебаний
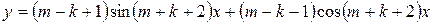
к виду  .
.
Найти амплитуду А, фазу  , период гармоники и построить ее график
, период гармоники и построить ее график
(т – предпоследняя цифра,  – последняя цифра учебного шифра).
– последняя цифра учебного шифра).
2. Решить систему линейных уравнений по формулам Крамера и методом Гаусса.
2.1 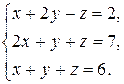 2.2
2.2 
2.3  2.4
2.4 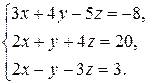
2.5 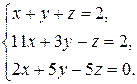 2.6
2.6 
2.7 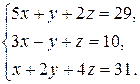 2.8
2.8 
2.9  2.10
2.10 
2.11  2.12
2.12 
2.13  2.14
2.14 
2.15 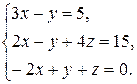 2.16
2.16 
2.17 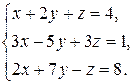 2.18
2.18 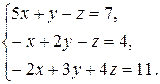
2.19  2.20
2.20 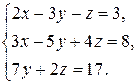
3. Определить тип кривой, найти ее параметры; определить угловой коэффициент прямой. Найти точки пересечения данных линий и сделать чертеж.
3.1 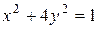 ;
; 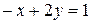 .
.
3.2  ;
; 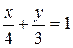 .
.
3.3  ;
;  .
.
3.4  ;
;  .
.
3.5  ;
;  .
.
3.6  ;
;  .
.
3.7 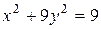 ;
; 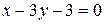 .
.
3.8  ;
;  .
.
3.9  ;
;  .
.
3.10  ;
; 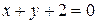 .
.
3.11  ;
; 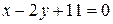 .
.
3.12 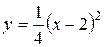 ;
;  .
.
3.13 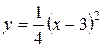 ;
;  .
.
3.14  ;
;  .
.
3.15  ;
; 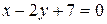 .
.
3.16 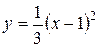 ;
;  .
.
3.17  ;
;  .
.
3.18  ;
; 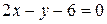 .
.
3.19 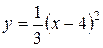 ;
;  .
.
3.20  ;
;  .
.
4. Даны координаты вершин пирамиды АВСD. Требуется:
1) записать векторы  в системе орт
в системе орт  и найти модули этих векторов;
и найти модули этих векторов;
2) найти угол между векторами  и
и  ;
;
3) найти проекцию вектора  на вектор
на вектор 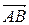 ;
;
4) найти площадь грани АВС;
5) найти объем пирамиды АВСD;
6) составить уравнение ребра АС;
7) составить уравнение грани АВС.
4.1 
4.2 
4.3 
4.4 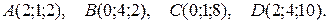
4.5 
4.6 
4.7 
4.8 
4.9 
4.10 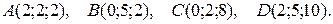
4.11 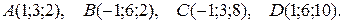
4.12 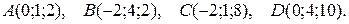
4.13 
4.14 
4.15 
4.16 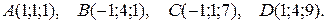
4.17 
4.18 
4.19 
4.20 
5. Функция у задана различными аналитическими выражениями для различных областей изменения аргумента х. Требуется:
1) Найти точки разрыва функции, если они существуют.
2) Найти односторонние пределы и скачок функции в точках разрыва.
3) Сделать чертеж.
5.1  5.2
5.2 
5.3  5.4
5.4 
5.5  5.6
5.6 
5.7 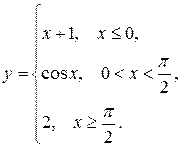 5.8
5.8 
5.9  5.10
5.10 
5.11 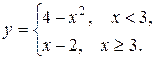 5.12
5.12 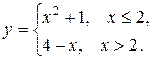
5.13  5.14
5.14 
5.15  5.16
5.16 
5.17  5.18
5.18 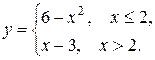
5.19 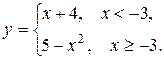 5.20
5.20 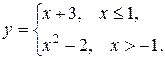
6. Построить кривые, заданные в полярной системе координат.
| 6.1 | ρ = (1 – сos φ). | 6.2 | 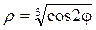 . .
| |
| 6.3 | ρ = 2 (1 – сos φ). | 6.4 | ρ = sin 2 φ. | |
| 6.5 | ρ = – (1 – сos φ). | 6.6 | ρ = 2 sin2 φ. | |
| 6.7 | ρ = 1 + сos φ. | 6.8 | ρ = 3 sin φ. | |
| 6.9 | ρ = 2 (1 + сos φ). | 6.10 | ρ = – 2 sin φ. | |
| 6.11 | ρ = 1 +sin φ. | 6.12 | ρ = 3 сos φ. | |
| 6.13 | ρ = 1 – sin φ. | 6.14 | ρ = – 3 сos φ. | |
| 6.15 | ρ = 2 (1 –sin φ). | 6.16 | ρ = sin φ. | |
| 6.17 | ρ = 2 (1 + sin φ). | 6.18 | ρ = сos φ. | |
| 6.19 |  . .
| 6.20 | ρ = sin 3 φ. |
7. Найти скорость  (м/с) и ускорение а (м/с2) материальной точки, траектория которой задана параметрическими уравнениями в момент времени
(м/с) и ускорение а (м/с2) материальной точки, траектория которой задана параметрическими уравнениями в момент времени 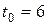 с.
с.
| 7.1 |  x = 4 сos x = 4 сos  y = 12 sin
y = 12 sin 
| 7.2 |  x = 8 sin x = 8 sin  – 2
y = 4 сos – 2
y = 4 сos  – 2 – 2
| |
| 7.3 |  х = 4 сos х = 4 сos  y = – 4 – 6 сos
y = – 4 – 6 сos 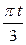
| 7.4 | 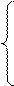 x = 8 sin x = 8 sin  – 2
y = 14 –16 сos 2 – 2
y = 14 –16 сos 2 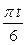
| |
| 7.5 |  x = 2 – 3 сos x = 2 – 3 сos  y = – 3 sin 2
y = – 3 sin 2 
| 7.6 |  x = 12 sin x = 12 sin  y = 14 – 16 сos
y = 14 – 16 сos 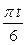
| |
| 7.7 |  x = 2 – 3 сos x = 2 – 3 сos  y = 9 sin
y = 9 sin  – 4 – 4
| 7.8 |  x = 8 sin x = 8 sin  – 2
y = 4 сos – 2
y = 4 сos 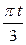
| |
| 7.9 |  x = 6 сos x = 6 сos  – 3
y = 3 сos – 3
y = 3 сos 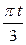 – 2 – 2
| 7.10 | 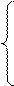 x = 12 sin x = 12 sin  y = – 10 сos
y = – 10 сos 
| |
| 7.11 |  x = 6 сos x = 6 сos  – 3
y = – 10 sin – 3
y = – 10 sin 
|  7.12
7.12
| x = 12 sin  y = – 4 сos 2
y = – 4 сos 2 
| |
| 7.13 |  x = 2 – 3 сos x = 2 – 3 сos  y = 2 – 6 sin 2
y = 2 – 6 sin 2 
| 7.14 |  x = 4 – 6 сos x = 4 – 6 сos  y = 8 – 12 сos
y = 8 – 12 сos 
| |
| 7.15 | x = 2 – 3 сos 
 y = 2 sin y = 2 sin  – 2 – 2
| 7.16 |  x = 4 – 6 sin x = 4 – 6 sin  y = 3 сos
y = 3 сos 
| |
| 7.17 |  x = 6 сos x = 6 сos  – 3
y = 9 сos – 3
y = 9 сos  + 5 + 5
| 7.18 |  x = 12 sin x = 12 sin  y = – 4 сos 2
y = – 4 сos 2 
| |
| 7.19 | 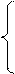 x = 4 сos x = 4 сos  y = 9 сos
y = 9 сos  + 5 + 5
| 7.20 | x = 8 sin  – 2 – 2
 y = 9 сos y = 9 сos  – 3 – 3
|
8. Провести полное исследование функции методами дифференциального исчисления и построить ее график.
8.1  . 8.2
. 8.2 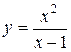 .
.
8.3  . 8.4
. 8.4  .
.
8.5  . 8.6
. 8.6  .
.
8.7  . 8.8
. 8.8  .
.
8.9 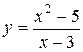 . 8.10
. 8.10  .
.
8.11  . 8.12
. 8.12  .
.
8.13 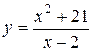 . 8.14
. 8.14  .
.
8.15  . 8.16
. 8.16 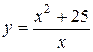 .
.
8.17 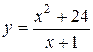 . 8.18
. 8.18  .
.
8.19 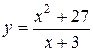 . 8.20
. 8.20  .
.
10. а) Вычислить площадь фигуры, ограниченной заданными параболами.
б) Найти объем тела, образованного вращением вокруг оси Ох фигуры, расположенной в первом квадранте и ограниченной заданными параболой, прямой и осью Ох.
10.1 а) 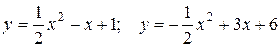 ; б)
; б) 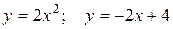 .
.
10.2 а) 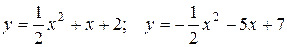 ; б)
; б)  .
.
10.3 а) 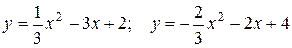 ; б)
; б)  .
.
10.4 а) 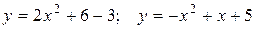 ; б)
; б) 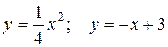 .
.
10.5 а)  ; б)
; б) 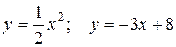 .
.
10.6 а)  ; б)
; б) 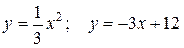 .
.
10.7 а)  ; б)
; б)  .
.
10.8 а)  ; б)
; б)  .
.
10.9 а)  ; б)
; б)  .
.
10.10 а)  ; б)
; б)  .
.
10.11 а)  ; б)
; б)  .
.
10.12 а)  ; б)
; б)  .
.
10.13 а)  ; б)
; б)  .
.
10.14 а)  ; б)
; б)  .
.
10.15 а)  ; б)
; б)  .
.
10.16 а)  ; б)
; б) 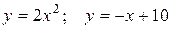 .
.
10.17 а)  ; б)
; б)  .
.
10.18 а)  ; б)
; б)  .
.
10.19 а)  ; б)
; б)  .
.
10.20 а)  ; б)
; б)  .
.
11. Даны дифференциальные уравнения второго порядка, допускающие понижение порядка. Найти частное решение, удовлетворяющее указанным начальным условиям.
11.1 
11.2 
11.3 
11.4 
11.5 
11.6 
11.7 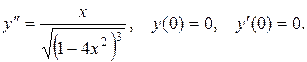
11.8 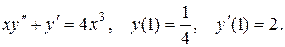
11.9 
11.10 
11.11 
11.12 
11.13 
11.14 
11.15 
11.16 
11.17 
11.18 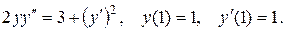
11.19 
11.20 
12. Классическим методом найти частное решение системы дифференциальных уравнений, удовлетворяющее начальным условиям.
12.1  12.2
12.2 
12.3 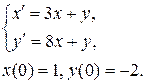 12.4
12.4 
12.5  12.6
12.6 
12.7 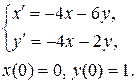 12.8
12.8 
12.9  12.10
12.10 
12.11  12.12
12.12 
12.13  12.14
12.14 
12.15  12.16
12.16 
12.17  12.18
12.18 
12.19 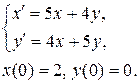 12.20
12.20 
13. Найти интервал сходимости степенного ряда и выяснить вопрос о сходимости ряда на концах интервала.
13.1 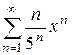 . 13.2
. 13.2  . 13.3
. 13.3  .
.
13.4  . 13.5
. 13.5  . 13.6
. 13.6  .
.
13.7  . 13.8
. 13.8  . 13.9
. 13.9  .
.
13.10 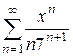 . 13.11
. 13.11  . 13.12
. 13.12  .
.
13.13  . 13.14
. 13.14  . 13.15
. 13.15  .
.
13.16 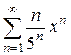 . 13.17
. 13.17  . 13.18
. 13.18  .
.
13.19  . 13.20
. 13.20 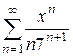 .
.
14. а) Найти разложение в степенной ряд по степеням х решения дифференциального уравнения (записать три первых отличных от нуля члена этого разложения).
14.1 а) 
|
14.2 а)  y (0) = 3; y (0) = 3; 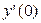 = 0,5 = 0,5
|
14.3 а)4 y ″ – xy = –3(x + 1)sin 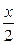 ; y (0) = 0; ; y (0) = 0; 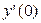 = 1,5 = 1,5
|
14.4 а) y ″ + xy′ – y = – xe–x – 1; y (0) = 2; 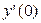 = 0 = 0
|
14.5 а) y ″ + y′ (x +2) = –2(x +2); y (0) = 0; 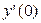 = 1,5 = 1,5
|
14.6 а)  y (0) = 0; y (0) = 0; 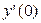 = –2 = –2
|
14.7 а) 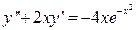 ; y (0)=0; ; y (0)=0; 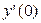 =1 =1
|
14.8 а)   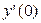 =1 =1
|
14.9 а)  ; y (0) = ; y (0) =  ; ; 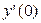 = 0 = 0
|
14.10 а)  ; y (0) = 0; ; y (0) = 0; 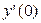 = 0 = 0
|
14.11 а)  ; y (0) = 1; ; y (0) = 1; 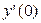 =1,5 =1,5
|
14.12 а) 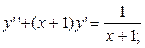 ; y (0) = 0; ; y (0) = 0; 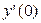 = 1,5 = 1,5
|
14.13 а)  ; y (0) = ; y (0) =  ; ; 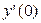 = = 
|
14.14 а)  ; y (0) = 0; ; y (0) = 0; 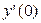 = –0,5 = –0,5
|
14.15 а) 
|
14.16 а) 
|
14.17 а) 
|
14.18 а) 
|
14.19 а) 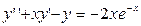 ; y (0) = 2; ; y (0) = 2; 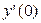 = –1 = –1
|
14.20 а) (x +1) y ″ + y′ = –1; y (0) = 0; 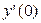 = – = – 
|
14. б) Разложить заданную функцию  в ряд Фурье по синусам на отрезке
в ряд Фурье по синусам на отрезке  и построить результирующую первых двух гармоник полученного ряда.
и построить результирующую первых двух гармоник полученного ряда.
14.1 б) 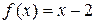 . 14.2 б)
. 14.2 б) 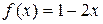 .
.
14.3 б) 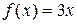 . 14.4 б)
. 14.4 б)  .
.
14.5 б)  . 14.6 б)
. 14.6 б)  .
.
14.7 б)  . 14.8 б)
. 14.8 б)  .
.
14.9 б) 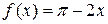 . 14.10 б)
. 14.10 б) 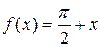 .
.
14.11 б)  . 14.12 б)
. 14.12 б)  .
.
14.13 б)  . 14.14 б)
. 14.14 б) 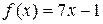 .
.
14.15 б)  . 14.16 б)
. 14.16 б)  .
.
14.17 б) 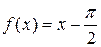 . 14.18 б)
. 14.18 б)  .
.
14.19 б) 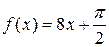 . 14.20 б)
. 14.20 б)  .
.
15. Дана функция двух переменных  . Найти:
. Найти:
1) экстремум функции  ;
;
2)  в точке А (1; –2);
в точке А (1; –2);
3) наибольшую скорость возрастания  точке А (1; –2).
точке А (1; –2).
15.1  .
.
15.2  .
.
15.3  .
.
15.4  .
.
15.5 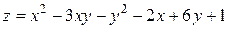 .
.
15.6 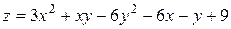 .
.
15.7 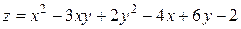 .
.
15.8  .
.
15.9 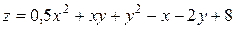 .
.
15.10 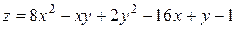 .
.
15.11  .
.
15.12  .
.
15.13  .
.
15.14  .
.
15.15 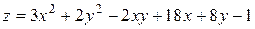 .
.
15.16  .
.
15.17 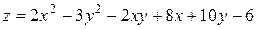 .
.
15.18 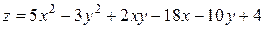 .
.
15.19 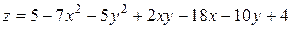 .
.
15.20  .
.
16. а) Найти объем тела, ограниченного параболоидом и цилиндром, через тройной интеграл, применяя цилиндрическую систему координат.
16.1 
16.2 
16.3 
16.4 
16.5 
16.6 
16.7 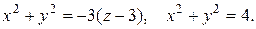
16.8 
16.9 
16.10 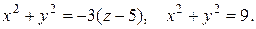
16. б) Найти объем тела, ограниченного сферой и конусом, через тройной интеграл, применяя сферическую систему координат.
16.11 
16.12 
16.13 
16.14 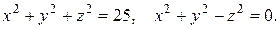
16.15 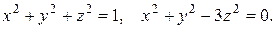
16.16 
16.17 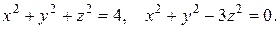
16.18 
16.19 
16.20 
17. а) С помощью двойного интеграла вычислить координаты центра тяжести фигуры (в задачах 17.1–17.10 взять меньшую по площади), ограниченной заданными линиями (поверхностную плотность считать равной единице).
17.1 а) 
17.2 а) 
17.3 а) 
17.4 а) 
17.5 а) 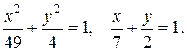
17.6 а) 
17.7 а) 
17.8 а) 
17.9 а) 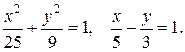
17.10 а) 
17.11 а) 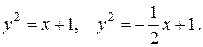
17.12 а) 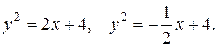
17.13 а) 
17.14 а) 
17.15 а) 
17.16 а) 
17.17 а) 
17.18 а) 
17.19 а) 
17.20 а) 
17. б) Найти поток векторного поля 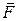 через полную поверхность пирамиды
через полную поверхность пирамиды  , образованной данной плоскостью
, образованной данной плоскостью 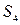 и координатными плоскостями
и координатными плоскостями  ,
,  ,
,  в направлении внешней нормали к ее поверхности, применив теорему Остроградского–Гаусса.
в направлении внешней нормали к ее поверхности, применив теорему Остроградского–Гаусса.
17.1 б) 
17.2 б) 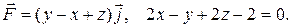
17.3 б) 
17.4 б) 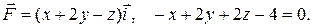
17.5 б) 
17.6 б) 
17.7 б) 
17.8 б) 
17.9 б) 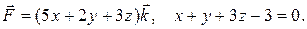
17.10 б) 
17.11 б) 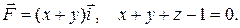
17.12 б) 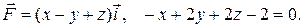
17.13 б) 
17.14 б) 
17.15 б) 
17.16 б) 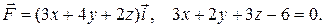
17.17 б) 
17.18 б) 
17.19 б) 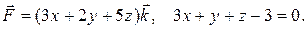
17.20 б) 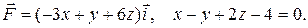
18. а) Вычислить работу, совершаемую переменной силой  по контуру, связывающему точки М (1; 2) и N (3; 5), и установить независимость от пути интегрирования.
по контуру, связывающему точки М (1; 2) и N (3; 5), и установить независимость от пути интегрирования.
18.1 а) 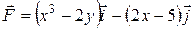 .
.
18.2 а)  .
.
18.3 а)  .
.
18.4 а)  .
.
18.5 а) 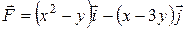 .
.
18.6 а) 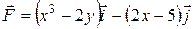 .
.
18.7 а)  .
.
18.8 а)  .
.
18.9 а)  .
.
18.10 а)  .
.
18.11 а)  .
.
18.12 а) 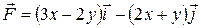 .
.
18.13 а) 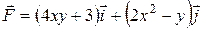 .
.
18.14 а)  .
.
18.15 а)  .
.
18.16 а)  .
.
18.17 а)  .
.
18.18 а)  .
.
18.19 а)  .
.
18.20 а) 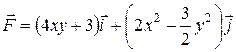 .
.
18. б) Дано векторное поле 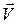 и точки
и точки  ,
,  и
и  .
.
1) Показать, что поле 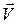 – потенциальное.
– потенциальное.
2) Найти потенциал  , если известно, что
, если известно, что  , где п – номер варианта.
, где п – номер варианта.
3) Найти работу поля между точками  и
и  ,
, 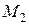 и
и  ,
,  и
и  и найти циркуляцию по контуру
и найти циркуляцию по контуру 


 .
.
18.1 б) 
 .
.
18.2 б) 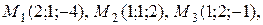
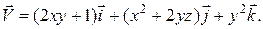
18.3 б)