1. Привести уравнения данных гармонических колебаний
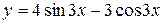
к виду  .
.
Найти амплитуду А, фазу  , период гармоники и построить ее график.
, период гармоники и построить ее график.
Решение. Привести уравнения данных гармонических колебаний

к виду  , где
, где  – амплитуда,
– амплитуда, 
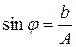 ,
,  и
и  – период колебания.
– период колебания.
В нашем случае:
 ,
,  и
и  ,
,  , откуда
, откуда  принадлежит 4 четверти и
принадлежит 4 четверти и  ,
,  . Тогда
. Тогда
 ,
,  .
.
От графика функции  перейдем к графику функции
перейдем к графику функции  с помощью следующей цепочки преобразований:
с помощью следующей цепочки преобразований:

то есть получим нашу функцию  .
.
Построение:
1. Строим одну волну синусоиды  .
.
2. Строим график функции  , которая имеет период
, которая имеет период  (то есть сжимаем функцию
(то есть сжимаем функцию 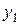 в три раза).
в три раза).
3. Увеличивая ординаты графика  в 5 раз, получаем график функции
в 5 раз, получаем график функции  .
.
4. 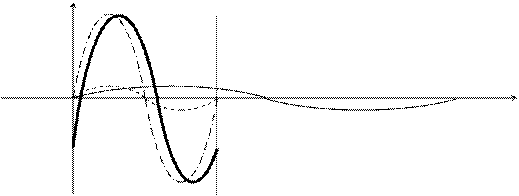 Сдвигаем график функции
Сдвигаем график функции  на 12,30 вправо вдоль оси Ох.
на 12,30 вправо вдоль оси Ох.
у
1200 132,30
0 12,30 600 1800 3600 х
у 2=sin3 x у 1=sin x
у 3=5sin3 x у =5sin(x– 12,30)
2. Решить систему линейных уравнений по формулам Крамера и методом Гаусса.

Решение. Решим систему линейных уравнений по формулам Крамера. Подсчитаем сначала главный определитель системы  , воспользовавшись следующим правилом вычисления определителей третьего порядка:
, воспользовавшись следующим правилом вычисления определителей третьего порядка:
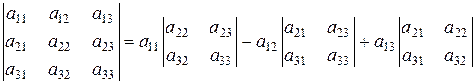 .
.

следовательно, данная система уравнений имеет единственное решение, которое находим по формулам Крамера:

где  получается путем замены i -го столбца свободными членами.
получается путем замены i -го столбца свободными членами.
Вычислим определители  .
.


 .
.
Находим 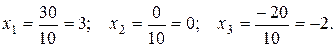
Ответ: 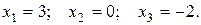
Решение системы линейных уравнений методом Гаусса (через расширенную матрицу).
Составим расширенную матрицу данной системы линейных уравнений и с помощью элементарных преобразований матрицы приведем ее к треугольному виду (ниже главной диагонали все элементы равны нулю).

Видим, что ранги матриц А и В совпадают и равны числу неизвестных, то есть  . Следовательно, система линейных уравнений имеет единственное решение. Чтобы найти это решение, перейдем от матричной записи к ступенчатой системе уравнений.
. Следовательно, система линейных уравнений имеет единственное решение. Чтобы найти это решение, перейдем от матричной записи к ступенчатой системе уравнений.

Двигаясь снизу вверх (обратный ход метода Гаусса), получаем  . Полученный результат подставляем во второе уравнение, а потом вместе с найденным
. Полученный результат подставляем во второе уравнение, а потом вместе с найденным  в первое уравнение:
в первое уравнение:

Ответ: 
3. Определить тип кривой  , найти ее параметры; определить угловой коэффициент прямой
, найти ее параметры; определить угловой коэффициент прямой  . Найти точки пересечения данных линий и сделать чертеж.
. Найти точки пересечения данных линий и сделать чертеж.
Решение. Приведем уравнение кривой  к каноническому виду
к каноническому виду  , разделив на 225. Получим уравнение эллипса
, разделив на 225. Получим уравнение эллипса  . Его большая полуось
. Его большая полуось  , малая полуось
, малая полуось  . Центр совпадает с началом координат.
. Центр совпадает с началом координат.
Уравнение прямой  имеет вид «в отрезках»
имеет вид «в отрезках»  , что удобно для построения. Для нахождения углового коэффициента прямой приведем ее к виду
, что удобно для построения. Для нахождения углового коэффициента прямой приведем ее к виду  , выразим у через х:
, выразим у через х:  .
.
Угловой коэффициент 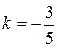 .
.
Для нахождения точек пересечения этих линий решим систему

Возведем второе уравнение в квадрат

и подставим в первое уравнение:


Нашли точки пересечения (0; 3) и (5; 0), что наглядно видно на чертеже.

 у
у


–5 0 5 х
–3
4. Даны координаты вершин пирамиды АВСD: 
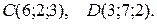 Требуется:
Требуется:
1) записать векторы  в системе орт
в системе орт  и найти модули этих векторов;
и найти модули этих векторов;
2) найти угол между векторами  и
и  ;
;
3) найти проекцию вектора 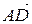 на вектор
на вектор  ;
;
4) найти площадь грани АВС;
5) найти объем пирамиды АВСD;
6) составить уравнение ребра АС;
7) составить уравнение грани АВС.
Решение.
1) Произвольный вектор  представляется в системе орт
представляется в системе орт 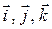 по формуле
по формуле  ,
,
где  – координаты вектора
– координаты вектора  . Если заданы точки
. Если заданы точки 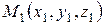 ,
,  , то для вектора
, то для вектора 
 ,
,
то есть
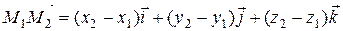 .
.
Воспользовавшись формулой и координатами заданных точек А, В, С, D, получим:
 ;
;
 ;
;
 .
.
Если вектор  , то его модуль вычисляется по формуле:
, то его модуль вычисляется по формуле:
 .
.
Модули найденных векторов
 ;
;
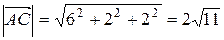 ;
;
 .
.
2) Известна формула
 ,
,
где 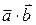 – скалярное произведение векторов
– скалярное произведение векторов  и
и 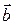 , которое можно вычислить следующим образом:
, которое можно вычислить следующим образом:
 .
.
У нас
 ,
,
то есть  .
.
3) Известно, что  ,
,
то есть в нашем случае
 .
.
4) Воспользуемся формулой нахождения площади треугольника, построенного на векторах  и
и 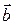
 ,
,
где  – векторное произведение векторов, которое можно вычислить по следующему правилу:
– векторное произведение векторов, которое можно вычислить по следующему правилу:
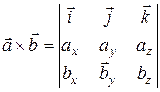 .
.
В нашем примере  , причем
, причем
 .
.
Таким образом,
 (кв. ед.).
(кв. ед.).
5) Объем пирамиды, построенной на трех некомпланарных векторах  , можно найти по формуле
, можно найти по формуле
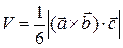 ,
,
где 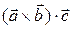 – смешанное произведение векторов, которое вычисляется следующим образом:
– смешанное произведение векторов, которое вычисляется следующим образом:
 .
.
У нас  , где
, где
 ,
,
то есть 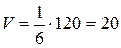 (куб. ед.).
(куб. ед.).
6) Известно, что уравнение прямой, проходящей через две заданные точки 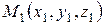 и
и  , имеет вид:
, имеет вид:
 .
.
Подставив координаты точек А и С, получим
 ,
,
то есть уравнение ребра АС окончательно запишется следующим образом:
 или
или  .
.
7) Уравнение плоскости, проходящей через три заданные точки  ,
, 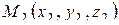 ,
,  , можно записать в виде
, можно записать в виде
 .
.
Подставляя в него координаты точек А, В, С, получим


5. Функция у задана различными аналитическими выражениями для различных областей изменения аргумента х:

Требуется: 1) найти точки разрыва функции, если они существуют, 2) найти односторонние пределы и скачок функции в точках разрыва, 3) сделать чертеж.
Решение. Данная функция определена и непрерывна в интервалах  . При
. При  и
и  меняется аналитическое выражение функции, и только в этих точках функция может иметь разрыв.
меняется аналитическое выражение функции, и только в этих точках функция может иметь разрыв.
Определим односторонние пределы в точке  :
:

Односторонние пределы совпадают. Функция в этой точке непрерывна.
Определим односторонние пределы в точке  :
:

Так как односторонние пределы функции у в точке  не равны между собой, то в этой точке функция имеет разрыв первого рода.
не равны между собой, то в этой точке функция имеет разрыв первого рода.
Скачком функции в точке разрыва называется абсолютная величина разности между ее правым и левым предельными значениями. Следовательно, в точке  скачок функции
скачок функции 
Построим график функции.

у
0 х
6. Построить кривые  в полярной системе координат.
в полярной системе координат.
Решение. Так как  , то
, то 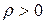 при любом значении
при любом значении  . Для каждого необходимого значения
. Для каждого необходимого значения  вычислим соответствующее значение
вычислим соответствующее значение  . Например: если
. Например: если  , то
, то  ; если
; если  , то
, то  . Результаты запишем в виде таблицы.
. Результаты запишем в виде таблицы.

| 
| 
| 
| 
| 
| 
| 
| 
| 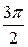
| 
| 
| 2 
| |

| 5,86 | 1,8 | 1,29 | 1,06 | 1,06 | 1,29 | 1,8 | 5,86 |
Построим кривую по полученным точкам.
 j = p/2 j = p/3 j = p/6
j = p/2 j = p/3 j = p/6
j = 0
0 4 9 r
Запишем уравнение данной кривой в прямоугольной декартовой системе координат:
 ,
, 
Обе части этого равенства принимают положительные значения, возведем их в квадрат:  .
.
Используем формулы:
 ,
,
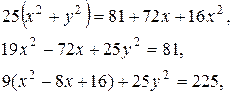
 – уравнение эллипса.
– уравнение эллипса.
С (4; 0) – центр эллипса,  полуоси эллипса.
полуоси эллипса.
7. Найти скорость  (м/с) и ускорение а (м/с2) материальной точки, траектория которой задана параметрическими уравнениями
(м/с) и ускорение а (м/с2) материальной точки, траектория которой задана параметрическими уравнениями

в момент времени  с.
с.
Решение. Вектор  есть радиус-вектор движущейся материальной точки. В нашем случае
есть радиус-вектор движущейся материальной точки. В нашем случае
 . Тогда вектор
. Тогда вектор  есть вектор скорости этой точки, который направлен по касательной к годографу данной линии в данной точке. В нашем случае
есть вектор скорости этой точки, который направлен по касательной к годографу данной линии в данной точке. В нашем случае

или 
В момент времени  с скорость материальной точки равна
с скорость материальной точки равна
 или
или 
 а величина скорости
а величина скорости 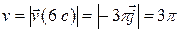 м/с.
м/с.
Как известно, вектор ускорения движения материальной точки равен
 В нашей задаче
В нашей задаче

 и
и  .
.
 .
.
8. Провести полное исследование функции  методами дифференциального исчисления и построить ее график.
методами дифференциального исчисления и построить ее график.
Решение.
1) Область определения функции  .
.
2) Исследование на непрерывность и классификация точек разрыва.
Заданная функция непрерывна всюду, кроме точки х = 4. Вычислим ее односторонние пределы в этой точке:

Таким образом, точка х = 4 является для заданной функции точкой разрыва второго рода, а прямая х = 4 – вертикальной асимптотой графика.
3) Исследование на экстремум и промежутки монотонности.

| х | 
| –2 | (–2; 4) | (4; 10) | 
| ||

| + | + | – | не сущ. | – | + | |

| 
| max | 
| 
| min | 
|
 .
.
4) Исследование графика на выпуклость, вогнутость, точки перегиба.

Так как  , то график заданной функции точек перегиба не имеет. Остается выяснить вопрос об интервалах его выпуклости и вогнутости:
, то график заданной функции точек перегиба не имеет. Остается выяснить вопрос об интервалах его выпуклости и вогнутости:
| х | 
| 
| |

| – | не сущ. | + |

| 
| 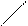
|
5) Исследование графика на наличие наклонных асимптот.

Таким образом, прямая  – наклонная асимптота графика.
– наклонная асимптота графика.
6) График заданной функции пересекает ось Оу в точке (0; –5).
По результатам исследования строим график.
 у
у
–4 0 4 х
9. Решить систему двух линейных уравнений в области комплексных чисел по формулам Крамера. Найденные  изобразить на комплексной плоскости;
изобразить на комплексной плоскости;  ,
,  записать в показательной и тригонометрической формах.
записать в показательной и тригонометрической формах.

Решение. Найдем решение системы линейных уравнений по формулам Крамера  . Для этого вычислим главный определитель системы
. Для этого вычислим главный определитель системы  и определители
и определители  , учитывая, что
, учитывая, что  – комплексное число, где
– комплексное число, где  .
.



Находим  :
:
 (т.к.
(т.к.  );
);

Таким образом, решение данной системы уравнений в алгебраической форме записи:

в векторной форме записи:

Для того, чтобы найти  в алгебраической форме, складываем действительные и мнимые части чисел
в алгебраической форме, складываем действительные и мнимые части чисел  :
:
 .
.
Вектор, соответствующий числу  , строим как сумму векторов по правилу параллелограмма.
, строим как сумму векторов по правилу параллелограмма.
Для того, чтобы найти  в алгебраической форме, вычитаем действительные и мнимые части чисел
в алгебраической форме, вычитаем действительные и мнимые части чисел  :
:
 .
.
Вектор, соответствующий числу  , записываем как сумму векторов
, записываем как сумму векторов  и
и  , строим его по правилу параллелограмма.
, строим его по правилу параллелограмма.

у
–3,5 z 2
j
– z 2 –203,5 x
z 1 z
и
Найдем модуль  и аргумент
и аргумент  комплексных чисел
комплексных чисел  (
( или
или  ;
;  в 1 и 4 четвертях;
в 1 и 4 четвертях;  во 2 и 3 четвертях, знак «+» или «–» выбираем так, чтобы аргумент был наименьшим по модулю).
во 2 и 3 четвертях, знак «+» или «–» выбираем так, чтобы аргумент был наименьшим по модулю).
Число  принадлежит 3 четверти:
принадлежит 3 четверти:
 (аргумент
(аргумент 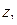 );
);

 (модуль
(модуль  ).
).
Число  принадлежит 1 четверти:
принадлежит 1 четверти:
 ;
;


Запишем числа  в показательной
в показательной  и тригонометрической
и тригонометрической  формах:
формах:

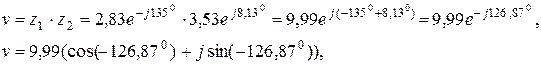
так как при умножении комплексных чисел их модули перемножаются, а аргументы складываются.

так как при делении комплексных чисел их модули делятся, а аргументы вычитаются.
10. а) Вычислить площадь фигуры, ограниченной заданными параболами  .
.
б) Найти объем тела, образованного вращением вокруг оси Ох фигуры, расположенной в первом квадранте и ограниченной заданными параболой  , прямой
, прямой  и осью Ох.
и осью Ох.
Решение.
а) Найдем абсциссы точек пересечения заданных парабол. Для этого приравняем правые части их уравнений:
 .
.
Отсюда 
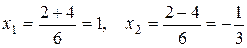 .
.

у
–1 0 1 х
Площадь вычислим по формуле
 ,
,
где  ,
,  – кривые, ограничивающие фигуру (
– кривые, ограничивающие фигуру ( ).
).
В нашем случае


б) Найдем абсциссу точки пересечения параболы и прямой в первом квадранте. Для этого решим уравнение
 ,
,
 ,
,
 .
.
Первому квадранту соответствует корень  .
.
Найдем теперь абсциссу точки пересечения прямой с осью Ох, решив уравнение  , откуда
, откуда  .
.
 Таким образом, можно считать, что тело вращения ограничено при
Таким образом, можно считать, что тело вращения ограничено при  поверхностью, образованной вращением параболы
поверхностью, образованной вращением параболы  вокруг оси Ох, а при
вокруг оси Ох, а при 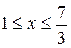 – вращением прямой
– вращением прямой  .
.
у
0 2 х
Объем ищем по формуле
 .
.
 .
.
Для вычисления второго интеграла используем подстановку  . Тогда
. Тогда  и
и  .
.
Отсюда
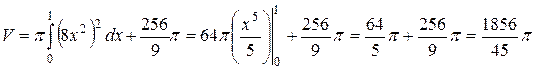 .
.
11. Найти частное решение дифференциального уравнения второго порядка, допускающее понижение порядка  , удовлетворяющее указанным начальным условиям
, удовлетворяющее указанным начальным условиям 
Решение. Данное дифференциальное уравнение второго порядка не содержит явно функцию у. Положим 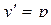 , где р – некоторая функция аргумента х. Если
, где р – некоторая функция аргумента х. Если  , то
, то  , и данное уравнение примет вид
, и данное уравнение примет вид  . Мы получили уравнение первого порядка относительно переменных р и х. Решим это уравнение:
. Мы получили уравнение первого порядка относительно переменных р и х. Решим это уравнение:

 , или
, или  .
.
Определим численное значение С 1 при указанных начальных условиях. Имеем  . Следовательно,
. Следовательно,  . Теперь решаем уравнение первого порядка
. Теперь решаем уравнение первого порядка  :
:

Определим численное значение С 2 при указанных начальных условиях. Имеем  .
.
Таким образом,  есть частное решение, удовлетворяющее указанным начальным условиям.
есть частное решение, удовлетворяющее указанным начальным условиям.
12. Классическим методом и методом операционного исчисления найти частное решение системы дифференциальных уравнений, удовлетворяющее начальным условиям.

Решение. Решением этой системы является пара функций  ,
,  , удовлетворяющих системе, причем
, удовлетворяющих системе, причем  .
.
1) Классический метод решения.
Продифференцируем первое уравнение по переменной  :
:
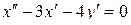 .
.
Из первого уравнения определяем  , следовательно, из второго уравнения имеем
, следовательно, из второго уравнения имеем
 .
.
Подставляем  в уравнение, полученное после дифференцирования, приходим к уравнению
в уравнение, полученное после дифференцирования, приходим к уравнению
 ,
,
 – линейное дифференциальное уравнение II порядка с
– линейное дифференциальное уравнение II порядка с
постоянными коэффициентами.
Составляем характеристическое уравнение и находим его корни:
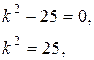
 – действительные различные корни.
– действительные различные корни.
В этом случае общее решение дифференциального уравнения имеет вид
 ,
,
 .
.
Ранее определили  . Тогда
. Тогда
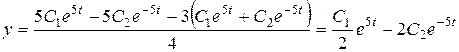 .
.
Общее решение системы

Находим значения произвольных постоянных, используя начальные условия  :
:

Частное решение системы

2) Метод операционного исчисления.
Пусть  . По теореме о дифференцировании оригинала получим
. По теореме о дифференцировании оригинала получим

Следовательно, операторная (изображающая) система имеет вид:

Из первого уравнения определяем

и подставляем во второе уравнение:


 ,
,
 .
.
Представим дробь в виде суммы простых дробей:


Следовательно,  .
.
По таблице изображений находим
 .
.
Аналогично:
 ,
,
 ,
,
 .
.
Частное решение системы

13. Найти область сходимости степенного ряда 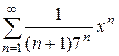 .
.
Решение. Общий член ряда  . Для исследования ряда на сходимость применим признак Даламбера:
. Для исследования ряда на сходимость применим признак Даламбера:
 .
.
Таким образом, при  , то есть при
, то есть при  исходный ряд сходится абсолютно.
исходный ряд сходится абсолютно.
Выясним вопрос о сходимости ряда на концах интервала сходимости. При  заданный ряд принимает вид
заданный ряд принимает вид
 .
.
Это числовой знакочередующийся ряд. Его общий член по абсолютной величине монотонно убывает и стремится к нулю при  . Таким образом, оба условия признака Лейбница выполнены и ряд сходится, то есть точка
. Таким образом, оба условия признака Лейбница выполнены и ряд сходится, то есть точка  принадлежит области сходимости заданного степенного ряда.
принадлежит области сходимости заданного степенного ряда.
При  исходный ряд принимает вид
исходный ряд принимает вид
 .
.
Это числовой знакоположительный ряд, который расходится (сравните его с гармоническим рядом 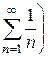 . Следовательно, точка
. Следовательно, точка  не принадлежит области сходимости заданного степенного ряда.
не принадлежит области сходимости заданного степенного ряда.
Таким образом, область сходимости исходного степенного ряда  . Вне этого интервала ряд расходится.
. Вне этого интервала ряд расходится.
14. а) Найти разложение в степенной ряд по степеням х решения дифференциального уравнения  (записать три первых отличных от нуля члена этого разложения).
(записать три первых отличных от нуля члена этого разложения).
Решение. Так как по условию  , то искомое частное решение
, то искомое частное решение  можно записать в виде:
можно записать в виде:
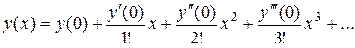
Из начальных условий уже известны  и
и  . Подставив эти значения в заданное уравнение, вычислим
. Подставив эти значения в заданное уравнение, вычислим  :
:
 .
.
Последовательно дифференцируя данное уравнение, будем иметь:

Теперь вычислим значения производных при  :
:
 .
.
Следовательно,
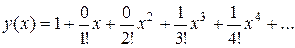
или
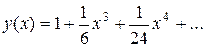
есть искомое частное решение.
14.б) Разложить заданную функцию  в ряд Фурье по синусам на отрезке
в ряд Фурье по синусам на отрезке  и построить результирующую первых двух гармоник полученного ряда.
и построить результирующую первых двух гармоник полученного ряда.
Решение. Так как по условию ряд должен содержать только синусы кратных углов, то следует продолжить заданную функцию на отрезок  нечетным образом, затем продолжить на всю числовую ось с периодом
нечетным образом, затем продолжить на всю числовую ось с периодом 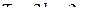 . Теперь разложим полученную периодическую функцию в ряд Фурье (эта операция разложения называется гармоническим анализом) вида:
. Теперь разложим полученную периодическую функцию в ряд Фурье (эта операция разложения называется гармоническим анализом) вида:
 .
.
Так как заданная функция нечетная, то коэффициенты ряда Фурье  , а
, а  вычисляем по формуле
вычисляем по формуле

и ряд Фурье имеет вид  .
.
Подставляя заданную функцию, получаем
 .
.
Последний интеграл вычисляем методом интегрирования по частям, полагая  . Отсюда
. Отсюда
 . Следовательно,
. Следовательно,