Тема: Дискретизация сигналов во времени. Теорема Котельникова.

Лекция №7

Содержание:

1. Случайные процессы и их основные характеристики.

2. Стационарные и нестационарные СП.

3. Особенности нестационарных процессов.

4. Функция корреляции «белого» с ограниченным спектром.

5. Эффективная ширина спектра.

Для количественного определения степени отличия сигнала и(t) и его смещенной во времени копии u(t-τ) принято вводить автокорреляционную функцию (АКФ) сигнала u(t), равную скалярному произведению сигнала и копии:

. (5.1)

В дальнейшем будем предполагать, что исследуемый сигнал имеет локализованный во времени импульсный характер, так что интеграл вида (3.15) заведомо существует.

К числу простейших свойств АКФ можно отнести ее четность:

B_u(τ)=B_u(-τ). (5.2)

Наконец, важное свойство автокорреляционной функции состоит в следующем: при любом значении временного сдвига т модуль АКФ не превосходит энергии сигнала:

. (5.3)

Итак, АКФ представляется симметричной кривой с центральным максимумом, который всегда положителен. При этом в зависимости от вида сигнала и(t) автокорреляционная функция может иметь как монотонно убывающий, так и колеблющийся характер.

Действительно, в соответствии с формулой (5.1) АКФ есть скалярное произведение: B_u(τ)=(u, u_τ). Здесь символом u_τ обозначена смещенная во времени копия сигнала и (t-τ).

Обратившись к обобщенной формуле Рэлея, можно записать равенство

.

Спектральная плотность смещенного во времени сигнала , откуда .

Таким образом, приходим к результату:

. (5.4)

Квадрат модуля спектральной плотности, как известно, представляет собой энергетический спектр сигнала. Итак, энергетический спектр и автокорреляционная функция связаны преобразованием Фурье:

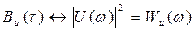. (5.5)

Ясно, что имеется и обратное соотношение:

. (5.6)

Эти результаты принципиально важны по двум причинам. Во-первых, оказывается возможным оценивать корреляционные свойства сигналов, исходя из распределения их энергии по спектру. Чем шире полоса частот сигнала, тем уже основной лепесток автокорреляционной функции и тем совершеннее сигнал с точки зрения возможности точного измерения момента его начала.

Во-вторых, формулы (5.4) и (5.6) указывают путь экспериментального определения энергетического спектра. Часто удобнее вначале получить автокорреляционную функцию, а затем, используя преобразование Фурье, найти энергетический спектр сигнала.

Обобщая формулу (5.1), назовем взаимокорреляционной функцией двух вещественных сигналов и(t) и v (t) скалярное произведение вида

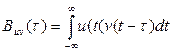(5.7)

Если в формуле (5.7) заменить переменную интегрирования, введя

х = t-τ, так что dt=dx, то, очевидно, возможна и такая запись:

. (5.8)

Поэтому

. (5.9)

В отличие от автокорреляционной функции одиночного сигнала, ВКФ, описывающая свойства системы двух неодинаковых сигналов, не является четной функцией аргумента τ: .

Если рассматриваемые сигналы имеют конечные энергии, то их взаимокорреляционная функция ограничена. Это утверждение следует из неравенства Коши — Буняковского:

,

откуда

, (5.10)

так как сдвиг сигнала во времени не влияет на значение его нормы.

Следует обратить внимание на то, что при τ=0 значения ВКФ вовсе не обязаны достигать максимума.

Выразим ВКФ двух сигналов через их спектральные характеристики. На основании обобщенной формулы Рэлея

и, поскольку спектр смещенного во времени сигнала 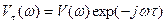, то

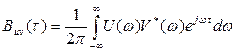
Имея в виду, что величина 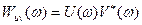есть взаимный энергетический спектр сигналов и (t) и v (t), определенный в бесконечном интервале частот -∞<ω<∞, приходим к выводу: взаимокорреляционная функция и взаимный энергетический спектр двух сигналов связаны парой преобразований Фурье.

В основе большинства методов исследования общей теории связи лежит представление о процессе передачи сообщения как некоторого случайного процесса, развивающегося (чаще всего) во времени. Словом случайный подчеркивается то обстоятельство, что предопределить зара­нее точное протекание процесса невозможно. По определению, случайный процесс Х(t)—это особого вида функция, характеризующаяся тем, что в любой момент времени t принимаемые ею значения являются случайными величинами. Типичным примером случайного процесса может служить напряжение Z(Q) = s(t) + N(t) на входе приёмника. Наблюдая напряжение в данный момент, мы не можем с полной определённо­стью предсказать, каково будет его значение в последующие моменты времени. Это объясняется тем, что параметры формируемого передатчиком канального сигнала s(t) (амплитуда, частота, фаза) изменяются случайным образом в соот­ветствии с передаваемым сообщением a(t). Кроме того, в процессе передачи сигнал подвергается воздействию различных аддитивных помех N(t), имеющих случайный характер, например в виде электрических разрядов в атмосфере, помех от электрического транспорта, помех от других радиостанций и т.д.

Случайность процесса X(t) проявляется в том, что вид наблюдаемой функции случайным образом меняется от одного наблюдения к другому. Однако получаемая в результате каждого отдельного опыта функция х(t) не случайна, её называют реализацией случайной функции. Случайный процесс представляет собой бесконечную совокупность таких реализации, образующих статистический ансамбль. На рис.5.1 показаны четыре реализации случайного процесса. Наличие случайности результатов многократных наблюдений одного и того же процесса не означает, что в этом процессе нет никаких закономерностей. Оказывается, что средние результаты, найденные по большому числу наблюдений, устойчи­вы. Иными словами, случайные явления и процессы подчиняются определён­ным статистическим закономерностям.

Если на графике множества реализации случайной функции Х(t) (рис.5.1) выбрать момент (сечение) t₁, то множество {х^(r)(t₁)} значений реализации в этот момент образует случайную величину X. Значения этой случайной вели­чины заранее неизвестны. Но можно установить некоторые закономерности, по которым можно судить о том, что в данном сечении случайная величина с вероятностью Р будет принимать значение в определённых пределах [x, x+∆x].

Для непрерывных процессов X(t) распределение вероятностей в заданном сечении t₁ характеризуется одномер­ной плотностью вероятностей (ПВ)

,

выражающей отношение вероятности того, что случайная величина X(t) примет значения в интервале , к величине интервала ∆х На рис. 5.2, а изображён типовой график одномерной ПВ.

Вероятность того, что случайная величина X примет значение в интервале (x₁;x₂ ) опреде­ляется выражением

.

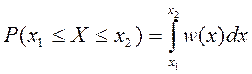Интеграл в бесконечных пределах от функции w(x) равен единице 1 (условие нормировки для достоверного события)

Другой важной характеристикой случайных величин Х является ИФР F(x), определяемая как вероятность того, что случайная величина X не превзойдёт некоторого значения х:

ИФР имеет следующие свойства:

1)F(-∞)=0;

2) F(∞)=1;

3) F(x) — неубывающая функция, т.е. F (x₂) ≥ F (x₁) при х₂ > x₁;

4) P[x₁≤X≤x₂]=F(x₂)- F(x₁)

График ИФР F{x) приведён на рис. 5.2, б.

В прикладных задачах часто предполагают, что ИФР являются дифференцируемыми функциями и определяют w(x) как производную от ИФР:

Для более полного описания случайного процесса нужно располагать его n-мерной плотно­стью вероятности w(x₁, x_2,…, x_n; t₁,t_2,…, t_n) или n-мерной ИФР F(x₁, x_2,…, x_n; t₁,t_2,…, t_n), выражающих свойства случайного процесса в произвольных сечениях t₁,t_2,…, t_n. В общем случае n-мерная ПВ определяется как

Для полного описания непрерывного во времени СП приходится п→∞.

Моменты, которые наблюдаются в сечениях процессов, зависят от временных аргументов, они получили название моментных функций.

Для статистической радиотехники наибольшее значение имеют три моментные функции низших порядков, называемые математическим ожиданием, дисперсией и функцией корреляции.