Группа – ЭТ-21-1 (ЗОТ) 15.12.2021
Дисциплина – Математика
Тема 1: Производная. Вычисление производных разных функций.
Записать конспект лекции с формулами и примерами решения в тетрадь. Решить задания для самостоятельного решения.
Не будем вдаваться в глубокие теоретические подробности. Вам надо просто научиться решать примеры на нахождение производной функции.
Определение: Производная – это скорость изменения функции.
Говоря совсем просто, для того чтобы найти производную функции, нужно по определенным правилам превратить её в другую функцию.
Посмотрите на Таблицу производных – там функции превращаются в другие функции. (Единственным исключением является экспоненциальная функция 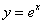 , которая превращается сама в себя.)
, которая превращается сама в себя.)
Операция нахождения производной называется дифференцированием.
Обозначения: Производную обозначают 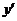 или
или 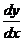 .
.
Таблица производных
| Правила дифференцирования
|
Запишите в тетрадь таблицы с формулами.
ВАЖНО!!!! При нахождении производных сначала используются правила дифференцирования, а затем – таблица производных элементарных функций (в левой колонке таблицы ищем функцию, а в правой –берем вид ее производной).
Еще раз: значек ¢(штрих) означает – найти производную.Если вы уже использовали формулу, то штрих больше ставить не надо.
Разбирая примеры, сначала прочитайте каждый. Не надо сразу подряд все записывать. Примеры разобраны очень подробно. В итоге вы должны записать условие и конечный вид решения.
|
|
ИТАК, знакомимся с правилами дифференцирования:
Постоянное число можно (и нужно) вынести за знак производной
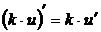 , где k – постоянное число (константа)
, где k – постоянное число (константа)
Пример 1. Найти производную функции 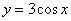
Решаем: 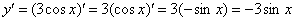
Производная суммы равна сумме производных
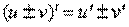
Пример 2 Найти производную функции 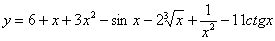
Решаем. Как Вы, наверное, уже заметили, первое действие, которое всегда выполняется при нахождении производной, состоит в том, что мы заключаем в скобки всё выражение и ставим штрих справа вверху:
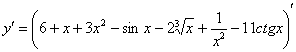
Применяем второе правило:
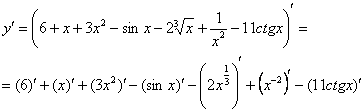
Все функции, находящиеся под штрихами, являются элементарными табличными функциями, с помощью таблицы осуществляем превращение.
Итоговая запись решения:

(Упрощаем полученные выражения)
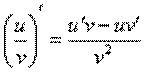
Производная произведения функций
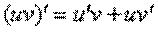
Пример 3
Найти производную функции 
В данной функции содержится сумма 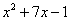 и произведение двух функций – квадратного трехчлена
и произведение двух функций – квадратного трехчлена 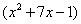 и логарифма
и логарифма 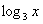 . Здесь всё так же. СНАЧАЛА мы используем правило дифференцирования произведения:
. Здесь всё так же. СНАЧАЛА мы используем правило дифференцирования произведения:
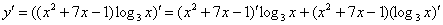
Теперь для скобки 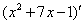 используем два первых правила:
используем два первых правила:
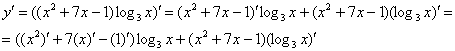
В результате применения правил дифференцирования под штрихами у нас остались только элементарные функции, по таблице производных превращаем их в другие функции. Итоговая запись решения:
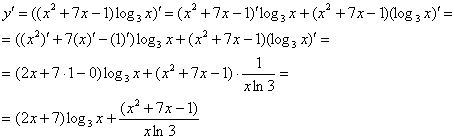
Производная частного функций
Пример 4 Найти производную функции 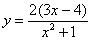
Решаем:
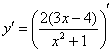
Теперь смотрим на выражение в скобках, как бы его упростить? В данном случае замечаем множитель, который согласно первому правилу целесообразно вынести за знак производной:
|
|
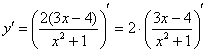
Смотрим на наше выражение в скобках. И здесь – сначала применяем правило дифференцирования частного:
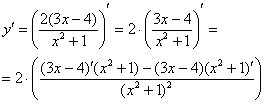
Таким образом, наша страшная производная свелась к производным двух простых выражений. Применяем первое и второе правило, здесь это сделаем устно, надеюсь, Вы уже немного освоились в производных:
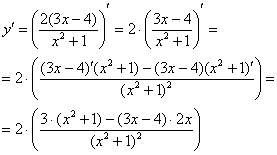
Штрихов больше нет, задание выполнено.
Вот какое решение получается:
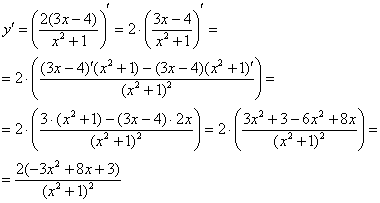
Выполните Задания для самостоятельного решения:
ВАЖНО!!!! При нахождении производных сначала используются правила дифференцирования, а затем – таблица производных элементарных функций.
1. Найти производную функции:
1) 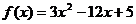
2) f(x) = 5ex – 2x4 + 7х;
3) у = х5× sinx;
4) у = 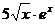
5) y = 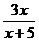 ;
;
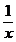
6) у = 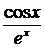 .
.
Надеюсь, что все понятно.
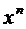
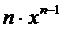
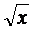
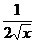
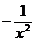

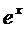
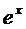
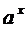
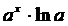

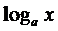
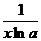
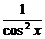
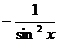
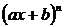
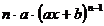
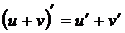 (производная суммы)
(производная суммы)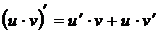 (производная произведения)
(производная произведения)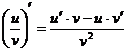 (производная частного)
(производная частного)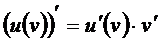 (производная сложной функции)
(производная сложной функции)