Примерные тестовые задания по дисциплине
«Основы финансовых вычислений»
Раздел 1. Теория процентов
1. За какой срок вклад в 100 тыс. руб. увеличится вдвое при ставке 10% годовых? (два ответа)
1) 20 лет
2) 10 лет
3) 7 лет
4) 30 лет
2. Hаращение первоначальной суммы (капитала) по сложным процентам называется:
1) мотивацией
2) девальвацией
3) капитализацией
3. Какова последовательность действий при прогнозировании финансовых процессов:
1) сбор необходимой статистической информации
2) расчет прогнозных значений экономического показателя
3) проверка условия адекватности
4) построение модели
5) проверка точности модели
4. При одной и той же ставке  наращение при сложной процентной ставке идет быстрее, чем при простой, при сроке операции меньше 1 года?
наращение при сложной процентной ставке идет быстрее, чем при простой, при сроке операции меньше 1 года?
1) да
2) нет
3) рост процентов одинаков
5. Как между собой соотносится текущая стоимость $100, получаемых через год: а) при простой процентной ставке 12,5%; б) при простой учетной ставке 12,5%?
1) (а)>(б)
2) (а)<(б)
3) (а)=(б)
6. При непрерывном начислении процентов наращенная сумма задается экспоненциальной функцией:
1) S=P e j∙t
2) S=P 
7. При дискретно изменяющейся во времени переменной процентной ставке наращенная сумма определяется по формуле (два ответа):
1) 
2) 
3) 
4)  ,
,
8. 100 тысяч рублей инвестированы на 5 лет по номинальной ставке 25% годовых. Когда наращенное значение больше?
1) при начислении один раз в год
2) при начислении два раза в год
3) при непрерывном начислении процентов по годовой ставке 25%.
9. 140 тысяч рублей инвестированы на два года по номинальной ставке 12% годовых. Когда наращенная сумма больше?
1) по годам
2) по полугодиям
3) по кварталам
4) no месяцам
10. По какой формуле определяется срок, на который должна быть инвестирована денежная сумма P под сложные проценты по ставке i за фиксированный период с целью накопления суммы S к концу этого периода?
1) 
2) 
3) 
11. По какой формуле определяется непрерывная ставка процентов?
1) 
2) 
3) 
12. Как называется величина (S-P), где S – заданная сумма, а Р – ее текущее значение:
1) сложным дисконтом
2) простым дисконтом
3) дисконтом (скидкой)
13. Если период ренты не совпадает с периодом начисления процентов, то она называется:
1) простой
2) сложной
3) общей
14. Необходимо положить 100 тысяч рублей, чтобы накопить к концу срока 700 тысяч рублей. Определить, какой срок больше, если
1) сложные проценты по ставке 25%
2) непрерывные проценты по ставке 8%
15. Каким уравнением воспользоваться для нахождения инфляции за квартал (x), если известна годовая инфляция  ?
?
1) 
2) 
3) 
16. Пусть результатом операции является денежный доход, равномерно распределенный от a до b, a<b. Каков риск этой операции?
1) 
2) 
3) 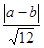
17. Учет кредитной организацией долговых обязательств это:
1) выкуп долговых обязательств до окончания срока их погашения;
2) перепродажа долговых обязательств до окончания срока их погашения;
3) досрочное исполнение долговых обязательств;
4) продление срока исполнения долговых обязательств.
18. Процентная ставка рассчитывается:
1) делением суммы процентов на будущую стоимость;
2) делением суммы процентов на текущую стоимость;
3) делением будущей стоимости на текущую;
4) делением текущей стоимости на будущую.
19. Процентная ставка – это:
1) доля суммы средств, вложенных в финансовую операцию, в сумме,
полученной по окончании финансовой операции;
2) доля процентов в сумме, полученной по окончании финансовой операции;
3) отношение суммы процентов от финансовой операции к сумме вложенных в нее средств;
4) количество раз превышения суммы, полученной по окончании финансовой операции, над суммой, вложенной в финансовую операцию.
20. Учетная ставка рассчитывается:
1) делением суммы дисконта на будущую стоимость;
2) делением суммы дисконта на текущую стоимость;
3) делением будущей стоимости на текущую;
4) делением текущей стоимости на будущую.
21. Учетная ставка – это:
1) доля суммы, вложенной в финансовую операцию, в сумме, полученной по окончании финансовой операции;
2) доля дисконта в сумме, полученной в результате операции;
3) соотношение суммы дохода от финансовой операции и суммы, вложенных в нее средств;
4) количество раз превышения суммы, полученной по окончании финансовой операции, над суммой, вложенной в финансовую операцию.
22. Синонимы термина «учетная ставка» (два ответа):
1) норма прибыли;
2) дисконт;
3) дисконтная ставка;
4) рост.
23. Синонимы термина «процентная ставка» (два ответа):
1) норма прибыли;
2) дисконт;
3) дисконтная ставка;
4) процент.
24. Чтобы привести длительность финансовой операции в соответствие с величиной ставки (процентной или учетной), надо ее выразить:
1) в днях;
2) в месяцах;
3) в кварталах;
4) в годах.
25. Синоним термина «приведенная стоимость» (два ответа):
1) сумма долга с процентами;
2) современная стоимость;
3) дисконтированная сумма;
4) наращенная сумма.
26. Синонимы термина «будущая стоимость» (два ответа):
1) сумма долга с процентами;
2) приведенная стоимость;
3) дисконтированная сумма;
4) наращенная сумма.
27. При одинаковой наращенной сумме процентная и учетная ставки:
1) равны;
2) процентная ставка меньше учетной;
3) процентная ставка больше учетной;
4) в различных ситуациях процентная и учетная ставки могут соотноситься по-разному.
28. Наращение это (два ответа):
1) расчет будущей стоимости с использованием процентной ставки;
2) расчет будущей стоимости с использованием учетной ставки;
3) расчет текущей стоимости с использованием процентной ставки;
4) расчет текущей стоимости с использованием учетной ставки.
29. Дисконтирование это (два ответа):
1) расчет будущей стоимости с использованием процентной ставки;
2) расчет будущей стоимости с использованием учетной ставки;
3) расчет текущей стоимости с использованием процентной ставки;
4) расчет текущей стоимости с использованием учетной ставки.
30. Временная база это:
1) длительность финансовой операции;
2) число дней в году;
3) период, в расчете на который задана ставка;
4) средняя длительность аналогичных финансовых операций.
31. Для простого процента характерно:
1) проценты начисляются на первоначальную сумму вклада, без учета
начисленных и не востребованных процентов;
2) в расчет принимается точное число дней в году;
3) проценты начисляются с общей суммы вклада, включая сумму ранее
начисленных и не востребованных процентов;
3) в расчет принимается приближенное число дней в году.
32. Для сложного процента характерно:
1) проценты начисляются на сумму вклада без процентов;
2) в расчет принимается точное число дней в году;
3) проценты начисляются на сумму вклада, включая сумму процентов;
4) в расчет принимается приближенное число дней в году.
33. Для точного процента характерно:
1) проценты начисляются на первоначальную сумму вклада, без учета
начисленных и не востребованных процентов;
2) в расчет принимается точное число дней в году;
3) проценты начисляются с общей суммы вклада, включая сумму ранее
начисленных и не востребованных процентов;
4) в расчет принимается приближенное число дней в году.
34. Для обыкновенного процента характерно:
1) проценты начисляются на первоначальную сумму вклада, без учета
начисленных и не востребованных процентов;
2) в расчет принимается точное число дней в году;
3) проценты начисляются с общей суммы вклада, включая сумму ранее
начисленных и не востребованных процентов;
4) в расчет принимается приближенное число дней в году.
35. Не используется в финансовых расчетах способ:
1) 360/360;
2) 360/365;
3) 365/365;
4) 365/360.
36. В числителе дроби, обозначающей сочетание способа определения длительности финансовой операции и способа определения количества дней в году, может указываться признак (два ответа):
1) точного числа дней финансовой операции;
2) приближенного числа дней финансовой операции;
3) приближенного числа дней в году;
4) точного числа дней в году.
37. В знаменателе дроби, обозначающей сочетание способа определения длительности финансовой операции и способа определения количества дней в году, может указываться признак (два ответа):
1) точного числа дней финансовой операции;
2) приближенного числа дней финансовой операции;
3) приближенного числа дней в году;
4) точного числа дней в году.
38. Если срок кредита 8 месяцев, простая процентная ставка 10 %, сумма
кредита 10 000 руб., то сумма процентов равна:
1) 667 руб.;
2) 800 руб.;
3) 6758 руб.;
4) 686 руб.
39. Процентное число рассчитывается:
1) умножением суммы вклада (без процентов) на количество дней нахождения его на счете;
2) умножением суммы вклада (без процентов) на временную базу;
3) умножением суммы вклада с процентами на количество дней пребывания
его на счете;
5) умножением суммы вклада с процентами на временную базу;
40. Если сумма вклада на счете меняется, то величина процентов определяется:
1) делением суммы процентных чисел на дивизор;
2) умножением суммы процентных чисел на дробь K/i;
3) сложением суммы процентных чисел и дивизора;
4) вычитанием из суммы процентных чисел дивизора.
41. При использовании простой процентной ставки сумма начисляемых процентов от одного периода их начисления к другому:
1) может изменяться по-разному;
2) уменьшается;
3) увеличивается;
4) не изменяется (одинакова в каждом периоде).
42. Для начисления процентов на первоначальную сумму потребительского
кредита характерно (два ответа):
1) уменьшение суммы погасительного платежа;
2) неизменная величина погасительного платежа;
3) увеличение суммы погасительного платежа;
4) применение «правила 78».
43. Под банковским дисконтированием понимается:
1) выдача банком векселя;
2) дисконтирование с использованием процентной ставки;
3) дисконтирование с использованием учетной ставки;
4) предоставление банком кредита.
44. Синонимом термина «коммерческое дисконтирование» не является:
1) банковское дисконтирование;
2) математическое дисконтирование;
3) банковский учет;
4) учет долговых обязательств.
45. Дисконт при учете векселя это:
1) скидка при приобретении векселя банком;
2) сумма процентов по векселю, причитающихся векселедержателю;
3) величина, определяемая умножением суммы, указанной в векселе, на учетную ставку и на длительность периода от учета до погашения векселя;
4) сумма, выплачиваемая векселедержателю при учете векселя.
46. Дисконтированная величина векселя это:
1) скидка при приобретении векселя банком;
2) сумма процентов по векселю, причитающихся векселедержателю;
3) величина, определяемая умножением суммы, указанной в векселе, на
учетную ставку за соответствующий период;
6) сумма, выплачиваемая векселедержателю при учете векселя.
47. Что понимают под процентами (процентными деньгами) в финансовых расчётах:
а) сотую долю суммы долга;
б) отношения суммы, выплаченной за пользованием кредита к величине долга;
в) абсолютную величину дохода от предоставления денег в долг?
48. Что понимают под процентной ставкой:
а) сумма, начисляемая за один год, на каждые 100 руб. основного долга;
б) отношение суммы процентных денег, выплачиваемых за фиксированный отрезок времени к величине ссуды;
в) абсолютная величина дохода от предоставления денег в долг?
49. Что понимают под периодом начисления:
а) один год;
б) интервал времени от момента получения кредита до полного погашения долга;
в) интервал времени, к которому относится процентная ставка?
50. Что понимают под наращенной суммой:
а) первоначальную сумму долга вместе с начисленными на неё процентами к концу срока;
б) сумму, начисленную за пользование кредитом;
в) доход, получаемый кредитором за год?
51. Что понимают под простыми процентами:
а) вариант расчёта, когда ставки процентов применяют к одной и той же начальной сумме, на протяжении всего срока ссуды;
б) вариант расчёта, когда ставки процентов применяют к сумме с начисленными в предыдущем периоде процентами;
в) вариант расчёта, когда ставки процентов меняются дискретно во времени?
52. Укажите формулу наращения по простым процентным ставкам:
а) 
б) 
в) 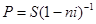
г) 
53. Укажите формулу для расчёта наращенной суммы, когда применяется простая процентная ставка, дискретно изменяющаяся во времени:
а) 
б) 

в) 
г) 
54. Укажите формулу математического дисконтирования в случае применения простой процентной ставки:
а) 
б) 
в) 
г) 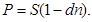
55. Укажите формулу банковского учета по простой учетной ставке:
а) 
б) 
в) 
г) 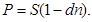
56. Что понимают под сложными процентами:
а) вариант расчёта процентов, при котором за базу измерения времени берут год, условно состоящий из 365 или 366 дней, а число дней ссуды в каждый месяц принимается равным 30;
б) вариант расчёта, при котором начисленные проценты присоединяют к сумме долга, а полученная сумма служит базой для очередного расчёта процентов;
в) вариант расчёта процентов, при котором производят капитализацию процентов?
57. Укажите формулу наращения по сложным процентным ставкам:
а) 
б) 
в) 
г) 
58. Как вычисляется наращенная сумма при применении сложных процентных ставок, если ставки дискретно меняются во времени:
а) 
б)  ;
;
в) 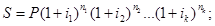
г) 
59. Укажите формулу математического дисконтирования по сложной процентной ставке:
а) 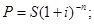
б) 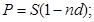
в) 
г) 
60. Укажите формулу банковского учёта по сложной учётной ставке:
а) 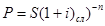
б) 
в) 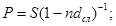
г) 