Вопрос. Индивидуальные и общие индексы

Понятие об индексах, их классификация

Индивидуальные и общие индексы

Средние индексы

Индексы средних уровней

 

Вопрос. Понятие об индексах, их классификация

Слово индекс «index» в переводе с латинского означает «указатель», «показатель».

Индекс - это относительный показатель, характеризующий изменение социально-экономического явления во времени, в пространстве или по сравнению с любым эталоном (нормативом, планом, прогнозом).

Индексы классифицируются по следующим направлениям:

- в зависимости от выбранной в знаменателе индекса базы сравнения;

- степени агрегирования (или охвата) явления;

- форме построения сводных индексов;

- характеру исследуемой величины;

- в зависимости от вида весов, выбранных в индексе;

- в зависимости от факторов, вызвавших изменение среднего уровня качественного показателя.

Экономическое содержание выбранной базы сравнения позво­ляет провести деление всех индексов на динамические, территориальные и плановые.

Динамические индексы предназначены для изучения изменения рассматриваемого явления во времени. При этом уровень базисного периода принято обозначать подстрочным символом «0», текущего (отчетного)- «1».

Многоуровневый динамический ряд позволяет исчислить цепные и базисные динамические индексы. В цепных индексах значение показателя текущего периода всегда сравнивается со значением предшествующего периода. В базисных выбирают определенный период за базу сравнения (чаще всего начальный уровень динамического ряда) и ведут рас­чет по отношению к нему.

Территориальные индексы используются для сравнительного анализа уровней социально-экономического развития отдельных территорий: стран, регионов, областей, районов.

Плановые индексы включают в себя индексы планового задания и индексы выполнения плана. Первый из них показывает степень увеличения (снижения) объемов производства по плану, второй - степень выполнения плана (достигнутая в отчетном пе­риоде величина сравнивается с запланированной). К этой же группе можно отнести индексы сравнения с нормативными значе­ниями или с определенным стандартом (эталоном, минимальным, мак­симальным или средним значениями показателя, характеризую­щего явление).

Индексы выражаются в коэффициентах и процентах.

 

вопрос. Индивидуальные и общие индексы

 

По степени охвата явления индексы бывают индивидуальные и общие. Индивидуальный индекс (i) характеризует изменение отдельного элемента, входя­щего в состав сложного явления, общий (I) выступает в качестве обобщенной характеристики изменения состояния разнородных единиц одной группы.

Простейшим показателем, используемым в индекс­ном анализе, является индивидуальный индекс, который харак­теризует изменение во времени (или в пространстве) отдельных элементов той или иной совокупности. Так, индивидуальный индекс цены рассчитывается по формуле:

 

,

 

где - цена товара в текущем периоде;

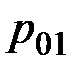- цена товара в базисном периоде.

 

Например, если цена товара А в текущем периоде составляла 30 руб., а в базисном 25 руб., то индивидуальный индекс цены

 

или 120%.

 

В данном примере цена товара А возросла по сравнению с базисным уровнем в 1,2 раза, или на 20%.

Оценить изменение объемов продажи товара в натуральных единицах измерения позволяет индивидуальный индекс физи­ческого объема реализации:

 

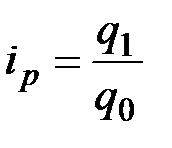
где - количество товара, реализованное в текущем периоде;

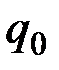- количество товара, реализованное в базисном периоде.

 

Индивидуальный индекс себестоимости единицы продукции показывает изменение себестоимости единицы продукции в отчетном периоде по сравнению с базисным.

где себестоимость единицы продукции отчетного периода,

себестоимость единицы продукции базисного периода.

Общие индексы характеризуют изменение социально - экономических явлений, отдельные элементы которых непо­средственно несоизмеримы.

В индексной теории используются две формы расчета свод­ных индексов: агрегатная форма и средние индексы. Основной формой является агрегатная, средние индексы получаются в результате ее преобразования.

Например, формула общего индекса цен в агрегатной форме имеет следующий вид:

 

где - товарооборот текущего периода,

- условная величина, показывающая, товарооборот отчетного периода при ценах базисного периода.

 

В любом агрегатном индексе различают два элемента:

1) индексируемая величина, т.е. величина, изменение которой показывает индекс;

2) веса (соизмерители) — постоянный элемент. Веса в числителе и в знаменателе фиксируются на уровне одного и того же периода.

В формуле общего индекса цен весами являются количество товаров каждого вида, реализованных в текущем периоде.

Следующий в этой системе - общий индекс физического объема реализации продукции.

 

где товарооборот отчетного периода по ценам базисного периода,

товарооборот базисного периода.

Общий индекс товарооборота - это сравнение товарооборота текущего периода с товарооборотом прошлого периода.

 

где 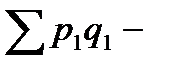товарооборот отчетного периода,

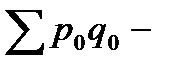товарооборот базисного периода.

 

 

Или через взаимосвязь

 

 

Величины, находящиеся в числителе и знаменателе агрегат­ных индексов, имеют вполне определенный экономический смысл: их разни­ца характеризует изменение явления в абсолютном выражении в отчетном периоде по сравнению с базисным.

Пример 1.

Имеются данные о продаже и ценах на продукцию на одном из рынков города:

Таблица 1

Продукт	Единица измерения	Продано, тыс. ед.	Цена единицы, руб.
в базисном периоде	в отчетном периоде	в базисном периоде	в отчетном периоде
Молоко Картофель Говядина	л кг кг

 

Определите:

1) общее изменение физического объема продаж;

2) общее изменение цен на указанные продукты;

3) общее изменение товарооборота в отчетном периоде по сравнению с базисным.

Решение:

1. Общий индекс объема продаж определим по агрегатной формуле индекса физического объема:

т.е. в отчетном периоде было продано продуктов на 9,6 % больше (109,6 % - 100 % =9,6 %), чем в базисном периоде.

1. Общий индекс цен, характеризующий среднее изменение цен на все продукты, определяем по формуле Пааше:

 

 

т.е. цены на все продукты повысились в среднем на 4,5 % (104,5% – 100%= 4,5%).

3. Общий индекс товарооборота определим, используя взаимосвязь индексов:

, т.е. товарооборот в целом возрос на 14,5 %

Вопрос. Средние индексы

Средний индекс - это сводный индекс, вычисленный как сред­невзвешенная величина из значений индивидуальных индексов.

Преобразование агрегатного индекса в средний из индивидуальных производится путем подстановки в числитель или знаменатель агрегатного индекса вместо индексируемой величины ее выражение через индивидуальный индекс. Если замена производится в числителе, то получают средний арифметический индекс из индивидуальных индексов. Если замена производится в знаменателе, то получают средний гармонический индекс из индивидуальных индексов.

Преобразуем агрегатный индекс физического объема товарооборота в средний арифметический индекс из индивидуальных индексов:

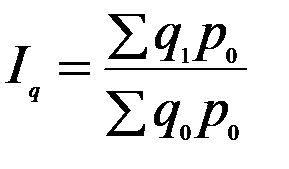, т.к. 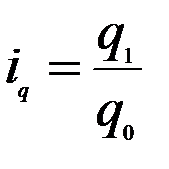, выразим 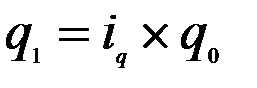и получим: - среднеарифметический индекс физического объема реализации

Аналогично для индекса цен:

. т.к. , выразим . Откуда - среднегармонический индекс цены.

Пример 1.

Определите среднее снижение цен на швейные изделия в отчетном периоде по сравнению с базисным по следующим данным:

 

 

Таблица 2

Наименование швейных изделий	Снижение цен в отчетном периоде по сравнению с базисным, %		Продано в отчетном периоде, млн. руб.
Хлопчатобумажные Капроновые	-20 -15	0,80 0,85	10,0 17,0

Решение:

В данном случае общий индекс цен может быть рассчитан из индивидуальных по формуле среднего гармонического индекса, тождественного агрегатному индексу Паше:

т.е., в среднем цены снизились на 16,9 % (83,1%-100% = -16,9%)

 

Пример 2.

Имеются следующие данные о выпуске продукции мебельной фабрики:

 

Наименование изделий	Изменение выпуска в мае по сравнению с апрелем, %	Выпуск продукции в апреле, млн. руб.,
Столы Диваны Стулья	+12 +10 +15	20,0 50,0 30,0

Определите увеличение выпуска всей продукции в мае по сравнению с апрелем (в %), т.е. рассчитать общий индекс физического объема.

Решение:

Общий индекс физического объема может быть рассчитан как средний арифметический:

 

т.е., в целом по предприятию выпуск продукции в мае по сравнению с апрелем увеличен на 11,9 %.