Здесь изучают различные способы представления графов в памяти компьютера. Они применяются во многих алгоритмах в задачах поиска информации. Существует несколько подходов к представлению данных в графе в памяти компьютера: матрицы, списки, коды.
Представление графов матрицами.
Напомним, что матрица – прямоугольная таблица чисел.
А= 
Aij – элемент i-строки, j-столбца.
Матрица размером m x n.
Если m=n – матрица называется квадратной.
В программе матрицы называют двумерными массивами.
Матрица смежности.
Опр. Пусть дан орграф с n пронумерованными вершинами. Матрица А размера m x n, заполненная числам 
, назывется матрицой смежности орграфа.
Она определяет орграф однозначно (по матрице можно восстановить граф)
Недостаток матрицы смежности – большое количество нулей (она разрешена).
Если у графа 10 вершин 20 дуг, то из 100 элементов матрицы 80 нулей.
Для неориентированного графа матрица смежности строится точно так же, но он обладает дополнительными хорошим свойствам.
aij=aji. Это свойство означает симметричность матрицы относительно главной диагонали.
В этом случае нет смысла хранить в память всю матрицу, достаточно ее верхний треугольник АI
Матрица смежности и число путей.
Заметим, что сама матрица смежности число путей длины 1 из i-й вершины в j-ю
j
i
Нельзя узнать число путей большей длины.
Вспомним операцию умножения матриц (умножение строк на столбцы). Если умножить квадратную матрицу саму на себя, получим квадрат матрицы А2=А*А: А3=А2*А и т. д.
Теорема Степень матрицы смежности Аm заполнена элементам aijm, показывает число путей длины m из i-й вершины в j-ю.
Доказательство
В частности случая m=2
А2=А*А заполнена произведениям строк на столбец aij=ai1*a1j+ai2*a2j+ain*anj= 0*0+0*1+1*1
Из этой суммы останется только члены 1*1, то есть aik=1 и akj=1.
Получим путь длины 2 из i-й вершины в j-ю, а вся сумма показывает нам число таких путей.
Аналогично доказывается для n=3,4 и т.д.
Матрица инцидентности.
Опр. Пусть в орграфе m вершин и n дуг (все пронумерованы).
Матрица B размером m x n заполняется числам
bij= 
Можно заметить, что в каждом столбце матрицы инцидентности встречается 1 и -1, остальные – нули (ил же 2 и остальные нули).
Поэтому и эти матрица тоже очень разряжена (при больших m)
Поэтому возникла мысль кроме матриц использовать отдельные числа (коды) для компактного представления графов.
Код Харари.
Идея Фрэнка Харари (США) – установить матрицу смежности в 1 число.
Пусть дан неориентированный граф. Мы уже знаем, что его матрица смежности А симметрична относительно главной диагонали м достаточно хранить её верхний треугольник АI. Распишем его в виде двоичной строки (слева направо, сверху вниз).
-> 0 1I 0I 0 1I 1
Меняем нумерацию вершин графа, точно так же получим другие двоичные строки (числа). Сравним между собой именно как число (по первому биту). Наибольшее из полученных чисел и есть код Харари, а нумерация вершин, давшая это число, называется канонической.
Код Харари определяет граф однозначно. При общении между людьми код Харари принято переводить в десятичное число.
Пример: Найти код Харари графа
А=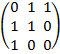 
AI= 
-> 0 1 1I 1 0I0
А= 
AI= 
-> 1 1 0I 0 1I 0
Вершину с петлей ставим первой, а соседнюю с ней – второй.
Очевидно, увеличить полученное число нельзя, значит, мы получили каноническую нумерацию вершин и код Харари. Переведём в десятичную систему. Получится 50.
Видимо, существует алгоритм, сразу нумерующий вершины графа каноническим образом (учитывая петли и число соседней (степен вершин)).
Заметим, что не всякое десятичное число служит кодом Харари какого-либо графа. Дело в том, что проделав все эти действия в обратном порядке, мы получим граф с нумерацией вершин, который вовсе не обязан быть канонической.
Деревья и ордеревья.
1)Существует особая вершина (корень дерева), в которую не входит не одна дуга.
2) во все остальные вершины входит одна единственная дуга
Вершины, из которых ни выходят дуги (не имеющие потомков) называются висячим.
Существует классификация вершин дерева по их расположению от корня.
Если вершину отделяет от корня k дуг, то говорят, что это вершина k-го уровня (яруса). Общее число уровней называется глубиной дерева (иногда высотой)
Опр. Связный граф, не имеющий цикла, называется деревом.
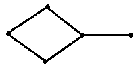
Дерево Не дерево
Понятие корня у дерева отсутствует
Существуют и другие определения дерева.
Теорема: Следующие свойства графа эквивалентны.
1) Граф является деревом.
2) Граф связан и Р=В-1
3) Граф не имеет циклов и Р=В-1
4) Граф связан, но утрачивает связность при удалении какого либо ребра (вершины остаются)
5) Граф не имеет циклов, но при добавлении любого нового ребра (но не вершин) циклы появляются.
Предположение: Если в орграфе удалить наконечники стрелок, то получится дерево.
Доказательство.
Так как во все вершины ордерева, кроме корня, входит единственная дуга, то число дуг равно В-1. Так как дуги превращаются в ребра, то теперь Р=В-1.
Так как каждая вершина дерева была соединен с корнем, то получившийся после ликвидации стрелок граф будет связный.
Согласно пункту 2 теоремы, полученный граф является деревом.
Из дерева можно получить ордерево, но уже многими способами.
Возникает впечатление, что у дерева все вершины как бы равноправны, но это не совсем так.
У дерева тоже есть понятие висячие вершины, вершина степени 1 называется висячей.
Классификация вершин дерева.
Опр. Расстояние от данной вершина А дерева до наиболее удаленной от нее вершины называется эксцентриситетом вершины А.
Радиус равен 3
Центр из 2 вершин
Наименьший из эксцентриситетов вершин является радиусом дерева, а множество вершин с этим наименьшим эксцентриситетом называется центром дерева.
Доказано, что центр дерева всегда состоит либо из одной вершины, либо из 2 смежных вершин.