Основные теории графов.
Из теории графов.
В 19 веке появилась потребность в математическом понятии для описания следующих рисунков.
 | |||
 | |||
Применение в физике для исследования электрических цепей, в химии для описания больших молекул. Так возникло понятие графа.
Вскоре выяснилось, что понятие графа имеет многочисленные примеры в самой математике и информатике (описание больших массивов, алгоритм сортировки и поиска в них).
Понятие графа и его составляющие.
Опр. Пусть дано множество X и многозначное отображение f:X->X. Тогда говорят, что задан ориентированный граф (орграф).
Элементами x c X называют вершинами орграфа узлами). Тогда (x;y),где у c f(x), называют дугой (изображается стрелкой).
 |
Последовательность дуг такая, что конец каждой дуги (кроме последней) является началом последующей, называют путем в орграфе.
Замкнутый путь называют контуром.
 |
Если в орграфе отождествить пары (x,y) и (y,x) (то есть «стереть» наконечники стрелок), то возникает неориентированный граф (граф).
Для него дуга переименовывается в ребро, путь – в цепь, контур – в цикл.
граф
ребро
 |
вершины цепь цикл
Замечание: в отличии от геометрических фигур, являющихся жесткими объектами, графы являются мягкими объектами (топологическими). Это означает, что ребра (дуги) графа можно рассматривать и изгибать, сохраняя лишь количество вершин и их соединений.
ð
=> 
Один и тот же граф.
Ясно, что в теории графов отсутствует понятие геометрической длины ребра (дуги). То есть все ребра (дуги) одинаковы. Если же ребра неравноправны, то на них ставят особые числа, называемые весом ребер (дуг).
Опр. Если каждому ребру (дуге) графа приписано некоторое число λк≥0 (вес ребра, дуги), то граф называется взвешенным (нагруженным).
Связные графы.
Опр. Неориентированный граф называется связным, если любые 2 его вершины можно соединить цепью.
Связный граф Несвязный граф
Попробуем разобраться в устройстве несвязных графов научно-математически. Нам поможет понятие отношения.
Опр: На множестве вершин графа X введем отношение Г: xГy, если x и Y можно соединить цепью.
Предложение: Отношение Г является отношением эквивалентности.
Доказательство.
Рефлексивно xГx - верно
Симметрично xГy => yГx - верно
Транзитивно xГy, yГz => - верно.
Значит это отношение эквивалентности. По теореме (свойство отношения эквивалентности) весь граф распадается на объединение непересекающихся классов эквивалентности, в каждом из которых любые 2 вершины можно соединить цепью. То есть весь граф распределяется на несколько непересекающихся свободных подграфов – компонент связности.
 | |||||
 | |||||
 |
Два компонента связности
Если же сам граф связан, то он состоит из одного компонента.
Поиск путей в графе.
Исторически сложилось 3 знаменитые задачи о поиске путей (цепей).
Задача № 1.
Это задача очевидна для небольших графов (для связных графов), но с увеличением графов задача становится все более сложней. Задача имеет возможное применение в теории игр (математическая теория, исследующая борьбу 2 сторон по заданным правилам).
Позиции данной игры изображаем вершинами графа, а ходы из одной позиции в другую – дугами (ребрами).
Проблема в том, чтобы найти любой путь из данной позиции в выигрышную.
Для небольших игр с несколькими позициями можно получить полное изображение игры в виде орграфа, найти на нем выигрышные и проигрышные позиции, разработать оптимальную стратегию игры.
Для больших игр (шахмат и т. д) даже современные компьютеры не позволяют получить полное описание игры и описания стратегии.
Задача № 2.
Найти кратчайший путь из A в B. (в смысле количество ребер или дуг).
Существует простой и эффективный алгоритм решения задачи 1 для любого графа. Будем постепенно присваивать вершинам графа целые числа – индексы.
Шаг 1
Вершине A присваиваем индекс 0.
Шаг 2.
Всем вершинам, смежным с A, присваиваем индекс 1.
Шаг 3.
Всем вершинам смежным с вершинам индекса 1 и не имеющим индекса присваиваем индекс 2. И так далее.
Процесс останавливается, когда вершина B получит некоторый индекс n (даже если остались вершины без индекса).
Число n- это и есть длина кратчайшего пути.
Шаг 4.
Среди вершин, смежных с B обязательно найдется вершина с С индексом n-1.Возвращаемся в С и повторим этот процесс.
Ровно через n шагов мы придем в вершину индекса 0, то есть А.
Вывод: Один или несколько путей построены.
Задача 3.Найти кратчайший путь из A в B во взвешенном графе, в смысле суммы весов всех ребер (дуг).
Существует эффективный алгоритм решения задачи 3 для любого взвешенного графа (поиск в ширину).
План.
Будем постепенно приписывать всем вершинам графа числовые индексы.
Шаг 1.
Вершине А припишем индекс 0, а всем остальным индексы +∞.
Замечание: в различных программах в качестве +∞ берут большое число, заведомо больше суммы всех весов графа.
Шаг 2.
Последовательно переберем все пары смежных вершин x и у.
Каждый раз, проверяя неравенство
ɱy>ɱx+λxy
Если оно выполняется, то уменьшим индекс ɱy заменив его на ɱx+λy
Шаг 3.
Процесс останавливается, когда ни один индекс уже не уменьшается.
В этот момент вершина B имеет некоторый индекс ɱB – это и есть наименьшая сумма весов.
Построим этот путь, возвращаясь из вершины B в вершину A.
Шаг 4.
Среди вершин, смежных с B обязательно найдется С, для которой выполняется точное равенство.
ɱB= ɱс+λСB
Возвращаемся в С и повторим этот процесс.
Так как при этом индексы все время уменьшаются, то через несколько шагов мы придем в вершину индекса 0, то есть в вершину A.
Один или несколько путей построены.
Задача коммивояжера.
Коммивояжер – коммерческий путешественник. Его задача – обойти заданные точки продаж с наименьшими затратами ресурсов.
Видим, что это задача из теории графов. Нужно построить путь (цепь), пропущенный через все вершины графов, с наименьшей суммой весов.
Видим, что задача коммивояжера обладает внутренним противоречием: с одной стороны нужно обойти все вершины, с другой минимизировать сумму весов. Поэтому простого и эффективного решения этой задачи до сих пор нет. Полный перебор все вариантов занимает очень много времени с ростом числа вершин.
Поэтому, проблема в том, чтобы отбрасывать заведомо плохие варианты, оставляя небольшое число «хороших».
Разработано несколько методов: метод ветвей и границ, сведение к задаче линейного программирования и т. д.
Но столь эффективного алгоритма, как для задачи 3, видимо, не существует.
Задача Эйлера.
Леонард Эйлер – великий математик, родившейся в Швейцарии, но проживающий в Санкт-Петербурге.
Начнем с детской задачи.
Нарисовать фигуру, не повторяя линии дважды.
Сформулируем её на языке теории графов: дан неориентированный граф. Требуется построить цепь, проходящую через все ребра ровно 1 раз (такая цепь называется Эйлерова).
Аналогично – задача построение Эйлерового цикла.
Задача Эйлера и состоит в том, чтобы выяснить, обладает ли данный граф Эйлеровой цепью или Эйлеровым циклом.
Как Эйлер пришел к этой задаче?
Задача о 7 мостах.
В городе Кенигсберг течет река, через которую проложено 7 мостов. Можно ли обойти все мосты ровно по 1 разу.
Видим, что и эта и та задачаиз теории графов.
Получим новый вид графа: так называемый мульти граф. В котором вершины могут быть соединены нескольким ребрами. Задача Эйлера имеет смысл и для мульти графа.
Эйлер решил эту задачу, введя простое понятие.
Степень вершин графа – это количество ребер, из нее исходящих (ей инцидентных).
- Степени вершин.
Теорема (Эйлера).
1)Связный граф обладает незамкнутой Эйлеровой цепью ó ровно 2 его вершины имеют нечетную степь.
2) Связный граф имеет, обладает незамкнутым Эйлеровым циклом ó все его вершины имеют четную степень.
Идея доказательства:
1)Пусть построена Эйлерова цепь
Видим, что 1 вершины нечетной степени – это начало и конец
Эйлеровой цепи.
2) Так как теперь начальная конечная вершины совпадают, то и вместе – четная.
Для небольших графов мы не нуждаемся в алгоритме, для больших – алгоритм прост.
Примеры.
1)Все вершины имеют четную степень, по теореме графов обладают Эйлеровым ц циклом. Начинать можно из любой вершины.
2)Видим 2 вершины нечетной степени, по теореме граф обладает незамкнутой 00 Эйнеровой цепью. В одной из них надо начинать, в другой заканчивать. Мы 0 1 построили незамкнутую Эйлерову цепь.
3) Имеем 4 вершины нечетной степени, по теореме графо не обладает ни Эй Эйлеровой цепью, ни Эйлеровым циклом.
То же самое- обойти 7 мостов невозможно.
2.6. Плоские графы и формула Эйлера.
Всякую ли фигуру можно «распутать»?
Опр. Граф называется плоским, если он расположен на плоскости и его ребра не пересекаются (кроме как в вершинах). Видим, что неплоский граф превратился в плоский. Поэтому определение не вполне корректное.
Поэтому усилим определение и дадим новое.
Опр. Граф называется планарным, если его можно расположить на плоскости так, что ребра не будут пересекаться.
Видим, что первоначальный граф был планарным.
Возникла проблема планарности: всякий ли неориентированный граф планарен (можно ли его распутать)
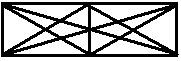Чтобы решить эту сложную проблему(выяснить,какие графы планарные, а какие нет), мы сначала изучим свойства планарных графов.
Формула Эйлера.
Для плоских графов введем новое понятие.
Опр. Грань плоского графа – часть плоскости, ограниченная его ребрами и не содержащая в себе ни ребер, ни вершин.
4 – в число граней всегда включают бесконечную грань.
Обозначим число граней плоского графа через Г. Также обозначается число его вершин В, чисор ребер Р.
Связаны ли между собой числа В,Г,Р?
Попробуем нащупать эту связь на практике.
1 пример. Уже нарисован.
Г=4; В=2; Р=6
2 пример
Г=2; В=4; Р=4
3 пример
Г=3; В=5; Р=6
Видим, что во всех 3 случаях В+Г-Р=2
Эйлер доказал, что это формула всегда верна.
Теорема(формула Эйлера)
Для любого плоского связного графа В+Г-Р=2.
Доказать ее в общем случае совсем не просто.
Замечание 1: Если плоский граф не связан, а состоит из k компонентов связности, то формула Эйлера усложняется
В+Г-Р=К+1
Замечание 2: Оказывается, формула Эйлера верна не только для плоских графов, но и для многогранников в пространстве. Дело в том, что любой многогранник можно превратить в плоский связанный граф (т.е. он планарен), растянув одну из его граней и спроецировав на плоскость.
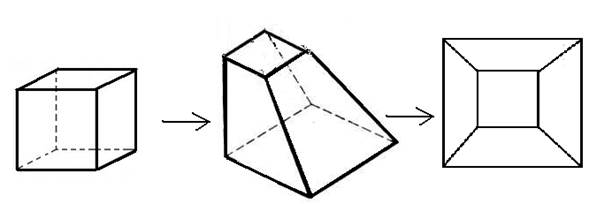
Ясно, что В и Р при этом не меняется, а число граней вроде бы меняется,: исчезает растянутая грань, но добавляется бесконечная. Значит, число Г так же не меняется, и формула Эйлера верна.
Замечание 3: Выразим из формулы Эйлера число граней
В-Р+Г=2 => Г=2-В+Р
Это позволяет для любого планарного графа заранее предсказать число граней, которое получится после его распутывания.
Пример: Дан планарный граф.
Предскажем число Г. Г=2+Р-2=2+11-6=7 граней
Распутаем граф и проверим.
Формула Эйлера – единственное равенство, верное для всех плоских графов. Но есть еще 2 равенства.
Теорема.
1)Для любого плоского связного графа (кроме 2 исключений 
и 
) верно неравенство
2Р≥ЗГ
2)Если к тому же среди значений нет ни одного треугольника. То неравенство усиливается.
2Р≥4Г
С одной стороны каждое ребро ограничивает не более 2 граней.
Значит
Г≤2Р
С другой стороны, каждая грань ограничена не меньше чем 3 ребрами(кроме 3 исключений 
)
Поэтому Р≥3Г
Из 2 неравенств следует 2Р≥ЗГ
Из 3 исключений неравенство случайно верно для графа 
Р=2, Г=1 (2*2>3*1). А 2 других так и остаются исключениями.
2)Если среди граней нет ни одного треугольника, то вместо Р≥3Г можем записать Р≥4Г.
Соответственно 2Р≥4Г.
Теперь можно доказать не планарность 2 исторически первых графов.
Граф № 1. (полный граф с 5 вершинами)
Граф № 2. (задача про 3 дома и 3 колодца)
Теорема: Графы № 1 и №2 не планарные.
Доказательство.
1)Допустим, что граф № 1 планарен. Тогда модем заранее предсказать число его граней Г.
В=5; Р=10 => Г=2+10-5=7
Подставим в неравенство
2Р≥3Г. Получим 20≥21 – неверно. Противоречием, граф не планарен.
2) Докажим,граф №2 планарен.
В=6; Р=9
Значит Г=2+Р-В=2+9-6=5
2Р≥3Г =. 18≥15 верно.
Но заметим, что среди граней не может быть ни одного треугольника.
- невозможно - невозможно
Четырехугольники теоритически могут быть.
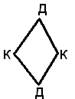
Поэтому неравенство усиливается 2Р≥4Г => 18≥20 - неверно. Противоречием, граф №2 не планарен. (чтд)
Теперь можем получить бесконечно много не планарных графов. Во-первых, можем добавлять на ребрах графов №1 и №2 любое число новых вершин.
Они, конечно, тоже непоанарны: если бы удалось их распутать, мы бы убрали добавленные вершины и заодно распутали бы графы №1 и № 2, что невозможно.
Во-вторых, можем добавлять к графам типа 1 и 2 новые ребра.
Построить принципиально новый не планарный граф никак не удавалось, пока не было доказано, что их не существует.
Теорема. Куратовского-Понтрягина.
Граф планарен ó он не содержит в себе графов типа 1 и 2.
Понятие о толщине графа.
Если граф не планарен, то разместить его в плоскости нельзя. Но можно разместить его в нескольких плоскостях.
Замечание: Этот прием имеет практическое применение при проектировании сложных микросхем. Дело в том, что каждая микросхема – плоский граф, так как разные компоненты не должны пересекаться.
Если же граф не планарен, приходиться размещать микросхему в нескольких плоскостях.
Опр. Толщиной графа t(Г) – наименьшее количество параллельных плоскостей. В которых можно разместить вершины графа так, чтобы его ребра не пересекались.
Ясно, что t(Г)=1 для планарных графов.
t(Г)=≥2 для не планарных графов.
К сожалению, точного равенства для толщины графа не существует, но имеется одно неравенство:
t(Г)≥ 1 + int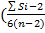 
, где n –число вершин графов, Si – степени его вершин, 
длина, int –целая часть действительного числа.
Замечание: в языках программирования употребляется не менее 3 операций, превращающих действительное число в целое.
1)int() – получает целое число слева от данного
int(-2,8) = -3
int(2,8) = 2
2)trunk()
trunk(2,8)=2
trunk(-2,8)=-2
3) round() – округление числа до ближайшего целого
round(2,8)=3
round(-2,8)=-3
Найдем толщину графа №1
N=5, si=4, ∑=4+4+4+4+4=20
t(Г)≥ 1 + int((
)=2
t(Г)≥2
Мы доказали другим способом, что граф непланарен.
Задачи о раскрасках графа.
На самом деле, это серьезные математические проблемы, так как расскарсить граф в N цветов – это то де самое, что присвоить его вершинам (ребрам) индексы от 1 до n, означающих номер цвета.
= неправильная раскраска.
О раскраске вершин орграфа.
Опр. Граф допускает правильную n-цветную раскраску вершин, если можно раскрасить вершины в n цветов так, что никакие 2 смежные вершины не окрашены одним цветом.
- правильно
Опр. Наименьшим числом n, при котором существует раскраска данного графа называется его хроматическим числом.
Проблема в том, что для любого графа найти его хроматическое число.
Некоторые легкие результаты
1)Полный граф с n вершинами имеет хроматическое число n.
n=5
2) Связный граф, не имеющий циклов(дерево), имеет хроматическое число 2. (можно раскрасить в 2 цвета).
Результат, близкий к полному решению проблемы:
Теорема Брукса (1941)
Если максимальная степень вершины графа равна d, то его хроматическое число hb≤d+1.
Однако, hb=d+1, только в 2 случаях
1)Граф является полным.
2)d=2. И при этом граф содержит цикл нечетной длины.
Цикл длины – 5
d=2 hb=3
В остальных случаях неравенство усиливается hb≤d.
Алгоритм решения задачи по раскраске вершин графа.
1)Вычислить степени свободы всех вершин в порядке убывания степеней. Присвоить n=1,
2)Окрасить первую неокрашенную вершину в цвет №1.
3)Окрасить в цвет № n все вершины, которые не смежным вершинам, уже окрашенным в цвет № n/
4)Если все вершины уже окрашены, то hb=n, иначе n:=n+1 и возвращаемся к шагу №2.
Отметим, что на шаге №3 мы перекрашиваем часть вершин.
Еще в 19 веке было замечено, что для любого плоскгого графа удается правильно раскрасить его не более чем в 4 цвета.
Однако, доказать это в общем случае не удавалось более 100 лет. Только в 1989 немецкие математики Аппель и Хамен смогли получить доказательство. Доказательство содержит более 100 страниц и его проверяли несколько лет.
О раскраске ребер графа.
Опр. Правильная раскраска ребер графа такая, что напоминает 2 инцидентные ребра (имеющие одну общую вершину) не окрашены в один цвет.
Минимальное число цветов, необходимое для правильной раскраски ребер, называется хроматическим индексом и обозначается hp.
Обозначим через d максимальную степень вершин графа. Ясно, что все ребра, инцидентные одной вершине, должны иметь разные цвета.
Откуда ясно, что hp ≥ d.
Основной результат доказан в 1946г. В.Г.Визингом (г. Одесса)
Для любого графа верно двойное неравенство
d≤hp≤d+1.
То есть либо hp=d, либо hp=d+1
Идея доказательства представляет собой алгоритм правильной раскраски ребер в наименьшие количество цветов(не более d+1). Оно основано на 2 операциях перекрашивания ребер. Встречаются оба случая hp=d и hp=d+1
Пример
d=2
hp=2
hp=d
d=2 
hp=2
hp=d+1
Вопросы к экзамену
12) Что такое граф, орграф. Вершина графов, дуга, ребро, путь, цепь, контур, цикл.
13)Каков алгоритм решения задачи о кратчайшем пути в невзвешенном графе?
14)Каков алгоритм решения задачи о кратчайшем пути во взвешенном графе?
15)Что такое Эйлерова цепь (цикл), у каких графов они существуют?
16) В чем состоит формула Эйлера и для каких объектов она верна?
17) Как выглядит не планарные графа №1 и №2, типов 1 и 2, в чем состоит теорема Куратовского-Понтрягина?
18)Что такое хроматическое число графа и что вы знаете о его величине?
19) Что такое хроматический индекс графа и что вы знаете о его длине.
Задачи могут быть к вопросам 13-15, 17-19.
Тема 3.