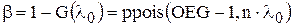| Контрольная величина | Название контрольной карты | Распределение контрольной величины |
| Число дефектов на товарную единицу продукции (число пятен на стекле, число дефектов изоляции на моток проволоки) | х – карта | Распределение Пуассона |
| Числу дефектов на некоторую условную единицу продукции (100 м проволоки, 1 кв. м. стекла) | u – карта | Распределение Пуассона |
| Число дефектных изделий в выборке | х – карта | Распределение Бернулли |
| Доля дефектных изделий (по отношению к объему выборки) | p – карта | Распределение Бернулли |
При контроле по числу дефектов в каждый момент взятия выборки проверяются гипотезы:
; процесс статистически подконтролен, среднее число дефектов на одно изделие 
в момент времени t не превышает требуемое значение 
,
; процесс статистически не подконтролен, среднее число дефектов на одно изделие в момент времени t превышает требуемое значение .
При контроле по числу дефектных изделий в каждый момент взятия выборки проверяются гипотезы:
; процесс статистически подконтролен, уровень дефектности процесса 
в момент времени t не превышает требуемое значение 
,
; процесс статистически не подконтролен, уровень дефектности процесса в момент времени t превышает требуемое значение 
.
Построение односторонней х – карты для числа дефектов на единицу продукции
Будем считать, что допустимое среднее число дефектов задано. Контрольная величина 
- накопленное число дефектов среди всех изделий в выборке. 
- величина целочисленная.
Необходимо определить:
объем выборки 
,
верхнюю контрольную границу 
,
верхнюю предупредительную границу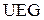 
.
Все эти величины опять же целочисленные.
Средняя М - линия проводится на уровне 
.
Контрольные границы вычисляются исходя из заданной вероятности ошибки первого рода 
, вероятности остановки хода процесса, остающегося статистически подконтрольным. Эта ошибка при контроле процессов называется вероятностью ложной тревоги.
Вероятность ложной тревоги определяется как вероятность того, что контрольная величина при контроле очередной выборки примет значение, превышающее контрольную границу 
:
.
Если задано, то, учитывая целочисленность значения , необходимо выполнение условия:
.
Величина подчиняется распределению Пуассона 
. Поэтому 
.
С учетом только что полученного равенства контрольную границу следует определять из условия:
.
При определении контрольной границы обычно принимают 
. Предупредительная граница определяется по той же формуле с вероятностью ошибки предупреждения 
.
Основная характеристика контрольной карты – функция мощности, зависимость вероятности срабатывания контрольной карты, то есть вероятности вмешательства в ход производственного процесса, от текущего значения показателя качества.
В случае использования односторонней контрольной карты для числа дефектов функция мощности определится как зависимость вероятности срабатывания контрольной карты от текущего значения параметра , текущего среднего числа дефектов на одно изделие:
.
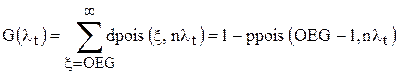Дополнение функции мощности до единицы – это вероятность невмешательства в ход процесса. Поэтому функция мощности позволяет получить выражение для вероятности ошибки второго рода – пропуска перехода:
