В) Электронные ресурсы.
1.Черненко В.Д. Высшая математика в примерах и задачах. Том 2 [Электронный ресурс]: учебное пособие/ Черненко В.Д.— Электрон. текстовые данные.— СПб.: Политехника, 2011.— 568 c.— Режим доступа: https://www.iprbookshop.ru/15891.— ЭБС «IPRbooks», по паролю
2.Черненко В.Д. Высшая математика в примерах и задачах. Том 1 [Электронный ресурс]: учебное пособие/ Черненко В.Д.— Электрон. текстовые данные.— СПб.: Политехника, 2011.— 709 c.— Режим доступа: https://www.iprbookshop.ru/15890.— ЭБС «IPRbooks», по паролю
Задачи для контрольной работы
Для задач №1 и №2 предварительно необходимо вычислить значения N и M для Вашего варианта. Если Ваш номер по списку равен 12, то 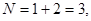 .
.  Если же полученные значения больше 10, то берется последняя цифра полученного значения. Например, для номера 29 имеем
Если же полученные значения больше 10, то берется последняя цифра полученного значения. Например, для номера 29 имеем 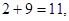
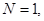


Задача 1.
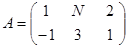 ,
,  ,
,  .
.
Вычислить: 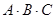 .
.
Задача 2

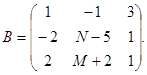
Вычислить: 
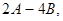
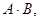

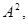

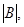
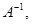
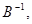
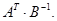
Найти решение системы линейных уравнений различными способами: а) методом обратной матрицы; б) с помощью формул Крамера; в) методом Гаусса.
| № варианта | № варианта | ||
| 1. |  – х1 + 2х2 + х3 = 5
2х1 – 3х2 + 3х3 = 1
х2 – 5х3 = – 9 – х1 + 2х2 + х3 = 5
2х1 – 3х2 + 3х3 = 1
х2 – 5х3 = – 9
| 2. |  3х1 − 9х2 + 8х3 = 5
2х1 − 5х2 + 5х3 = 4 3х1 − 9х2 + 8х3 = 5
2х1 − 5х2 + 5х3 = 4
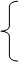 2х1 − х2 + х3 = −4 2х1 − х2 + х3 = −4
|
| 3. |  – 2х2 – 5х3 = – 12
– 2х1 – х2 + 3х3 = 7
– х1 + х2 + х3 = 4 – 2х2 – 5х3 = – 12
– 2х1 – х2 + 3х3 = 7
– х1 + х2 + х3 = 4
| 4. | х1 + 3х2 − 2х3 = − 5 х1 + 9х2 − 4х3 = −1 −2х1 + 6х2 − 3х3 = 6 |
| 5. |  – 3х1 + х2 + 3х3 = 10
– 2х2 – х3 = – 4
2 х1 – х2 + 3х3 = 3 – 3х1 + х2 + 3х3 = 10
– 2х2 – х3 = – 4
2 х1 – х2 + 3х3 = 3
| 6. |  2х1 + 3х2 + х3 = 4
4х1 − х2 + 5х3 = 6
х1 − 2х2 + 4х3 = 9 2х1 + 3х2 + х3 = 4
4х1 − х2 + 5х3 = 6
х1 − 2х2 + 4х3 = 9
|
| 7. |  – х1 + 2х3 = 5
2х1 + 2х2 + 5х3 = 10
3х1 – 2х2 + 2х3 = – 1 – х1 + 2х3 = 5
2х1 + 2х2 + 5х3 = 10
3х1 – 2х2 + 2х3 = – 1
| 8. | 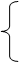 −2х1 + х2 − 3х3 = −4
4х1 + 7х2 − 2х3 = − 6
х1 − 8х2 + 5х3 = 1 −2х1 + х2 − 3х3 = −4
4х1 + 7х2 − 2х3 = − 6
х1 − 8х2 + 5х3 = 1
|
| 9. |  2х1 – х2 – 6х3 = –15
3х1 – х2 + х3 = – 2
– х1 + 3х3 = 7 2х1 – х2 – 6х3 = –15
3х1 – х2 + х3 = – 2
– х1 + 3х3 = 7
| 10. | 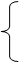 х1 + 7х2 − 2х3 = 3
3х1 + 5х2 + х3 = 5
−2х1 + 5х2 − 5х3 = −4 х1 + 7х2 − 2х3 = 3
3х1 + 5х2 + х3 = 5
−2х1 + 5х2 − 5х3 = −4
|
| 11. |  – х1 + х2 – х3 = 0
3х1 – 4х2 + 3х3 = –1
–2х2 – 3х3 = – 8 – х1 + х2 – х3 = 0
3х1 – 4х2 + 3х3 = –1
–2х2 – 3х3 = – 8
| 12. | 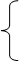 3х1 + 4х2 + 2х3 = 8
2х1 − 4х2 − 3х3 = − 1 3х1 + 4х2 + 2х3 = 8
2х1 − 4х2 − 3х3 = − 1
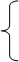 х1 + 5х2 + х3 = 0 х1 + 5х2 + х3 = 0
|
| 13. |  2х1 – х2 + х3 = –1
– х1 + 3х3 = 7
х1 + х2 + 3х3 = 6 2х1 – х2 + х3 = –1
– х1 + 3х3 = 7
х1 + х2 + 3х3 = 6
| 14. | 5х1 + 8х2 − х3 = 7 2х1 − 3х2 + 23 = 9 х1 + 2х2 + 3х3 = 1 |
| 15. | 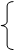 3х1 – 2х2 = – 5
х1 – 2х2 + х3 = – 1
х1 + 3х2 – х3 = 0 3х1 – 2х2 = – 5
х1 – 2х2 + х3 = – 1
х1 + 3х2 – х3 = 0
| 16. |  3х1 + х2 + х3 = 21
х1 − 4х2 − 2х3 = − 16 3х1 + х2 + х3 = 21
х1 − 4х2 − 2х3 = − 16
 −3х1 + 5х2 + 6х3 = 41 −3х1 + 5х2 + 6х3 = 41
|
| 17. |  х1 – 3х2 + х3 = –2
х1 – 2х2 – 4х3 = –11
–2х1 – х2 = 1 х1 – 3х2 + х3 = –2
х1 – 2х2 – 4х3 = –11
–2х1 – х2 = 1
| 18. | 2х1 − х2 + 5х3 = 4 5х1 + 2х2 + 13х3 = 2 3х1 − х2 + 5х3 = 0 |
| 19. | 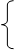 – х1 + 3х2 = 4
3х1 − 2х2 + х3 = − 3
2х1 + х2 − х3 = – 3 – х1 + 3х2 = 4
3х1 − 2х2 + х3 = − 3
2х1 + х2 − х3 = – 3
| 20. |  х1 + х2 − х3 = − 2
4х1 − 3х2 + х3 = 1
2х1 + х2 − х3 = 1 х1 + х2 − х3 = − 2
4х1 − 3х2 + х3 = 1
2х1 + х2 − х3 = 1
|
| 21. |  4х1 + 7х2 − 3х3 = − 10
2х1 + 9х2 − х3 = 8
−х1 + 6х2 − 3х3 = 3 4х1 + 7х2 − 3х3 = − 10
2х1 + 9х2 − х3 = 8
−х1 + 6х2 − 3х3 = 3
| 22. 
| 7х1 − 5х2 = 34 4х1 + 11х2 = − 36 2х1 + 3х2 + 4х3 = − 20 |
| 23. |  х1 − 5х2 + 3х3 = − 1
2х1 + 4х2 + х3 = 6
−3х1 + 3х2 − 7х3 = − 13 х1 − 5х2 + 3х3 = − 1
2х1 + 4х2 + х3 = 6
−3х1 + 3х2 − 7х3 = − 13
| 24. 
| х1 + 2х2 + х3 = 4 3х1 − 5х2 + 3х3 = 1 2х1 + 7х2 − х3 = 8 |
| 25. |  2х1 + 4х2 − 3х3 = − 10
−х1 + 5х2 − 2х3 = 5
3х1 − 2х2 + 4х3 = 3 2х1 + 4х2 − 3х3 = − 10
−х1 + 5х2 − 2х3 = 5
3х1 − 2х2 + 4х3 = 3
| 26. 
| х1 + х2 − х3 = 1 8х1 + 3х2 − 6х3 = 2 −4х1 − х2 + 3х3 = − 3 |
| 27. |  − 2х1 + 5х2 − 6х3 = − 8
х1 + 7х2 − 5х3 = − 9
4х1 + 2х2 − х3 = − 12 − 2х1 + 5х2 − 6х3 = − 8
х1 + 7х2 − 5х3 = − 9
4х1 + 2х2 − х3 = − 12
| 28. |  х1 − 2х2 + 3х3 = 6
2х1 + 3х2 − 4х3 = 20
3х1 − 2х2 − 5х3 = 6 х1 − 2х2 + 3х3 = 6
2х1 + 3х2 − 4х3 = 20
3х1 − 2х2 − 5х3 = 6
|
| 29. |  − 3х1 + 5х2 − 6х3 = − 5
2х1 − 3х2 + 5х3 = 8
х1 + 4х2 − х3 = 1 − 3х1 + 5х2 − 6х3 = − 5
2х1 − 3х2 + 5х3 = 8
х1 + 4х2 − х3 = 1
| 30. |  4х1 − 3х2 + 2х3 = 8
2х1 + 5х2 − 3х3 = 11
5х1 + 6х2 − 2х3 = 13 4х1 − 3х2 + 2х3 = 8
2х1 + 5х2 − 3х3 = 11
5х1 + 6х2 − 2х3 = 13
|
Найти общее решение однородной системы линейных уравнений.
| № варианта | № варианта | ||
| 1. |  3х1 – 5х2 – х3 – 2х4 = 0
8х1 – 6х2 + 3х3 – 7х4 = 0
2х1 + 4х2 + 5х3 – 3х4 = 0 3х1 – 5х2 – х3 – 2х4 = 0
8х1 – 6х2 + 3х3 – 7х4 = 0
2х1 + 4х2 + 5х3 – 3х4 = 0
| 2. |  3х1 + 2х2 – х3 – 9х4 = 0
5х1 – 3х2 + 4х3 – 3х4 = 0
х1 + 7х2 – 6х3 – 15х4 = 0 3х1 + 2х2 – х3 – 9х4 = 0
5х1 – 3х2 + 4х3 – 3х4 = 0
х1 + 7х2 – 6х3 – 15х4 = 0
|
| 3. |  3х1 + х2 – 3х3 – 10х4 = 0
4х1 + 5х2 – 7х3 – 20х4 = 0
2х1 – 3х2 + х3 = 0 3х1 + х2 – 3х3 – 10х4 = 0
4х1 + 5х2 – 7х3 – 20х4 = 0
2х1 – 3х2 + х3 = 0
| 4. |  х1 + 3х2 – х3 – 6х4 = 0
7х1 + 3х2 + 2х3 – 15х4 = 0
5х1 – 3х2 + 4х3 – 3х4 = 0 х1 + 3х2 – х3 – 6х4 = 0
7х1 + 3х2 + 2х3 – 15х4 = 0
5х1 – 3х2 + 4х3 – 3х4 = 0
|
| 5. |  х1 + х2 – 3х3 – 6х4 = 0
7х1 – 3х2 – 7х3 – 18х4 = 0
4х1 – х2 – 5х3 – 12х4 = 0 х1 + х2 – 3х3 – 6х4 = 0
7х1 – 3х2 – 7х3 – 18х4 = 0
4х1 – х2 – 5х3 – 12х4 = 0
| 6. |  х1 + 3х2 + 4х3 – х4 = 0
5х1 – 7х2 – 2х3 – 5х4 = 0
3х1 – 2х2 + х3 – 3х4 = 0 х1 + 3х2 + 4х3 – х4 = 0
5х1 – 7х2 – 2х3 – 5х4 = 0
3х1 – 2х2 + х3 – 3х4 = 0
|
| 7. |  х1 + 4х2 – 3х3 – 9х4 = 0
3х2 – 7х3 – 10х4 = 0
2х1 + 5х2 + х3 – 8х4 = 0 х1 + 4х2 – 3х3 – 9х4 = 0
3х2 – 7х3 – 10х4 = 0
2х1 + 5х2 + х3 – 8х4 = 0
| 8. |  2х1 – 2х2 + 3х3 + х4 = 0
5х1 – 2х2 + 4х3 – 4х4 = 0
х1 + 2х2 – 2х3 – 6х4 = 0 2х1 – 2х2 + 3х3 + х4 = 0
5х1 – 2х2 + 4х3 – 4х4 = 0
х1 + 2х2 – 2х3 – 6х4 = 0
|
| 9. |  х1 + 3х3 + х4 = 0
3х1 – 2х2 + 8х3 + 4х4 = 0
– х1 + 2х2 – 2х3 – 2х4 = 0 х1 + 3х3 + х4 = 0
3х1 – 2х2 + 8х3 + 4х4 = 0
– х1 + 2х2 – 2х3 – 2х4 = 0
| 10. |  2х1 – 2х2 + х3 – х4 = 0
2х1 – 3х2 + 5х3 + 4х4 = 0
– 2х1 + х2 + 3х3 + 6х4 = 0 2х1 – 2х2 + х3 – х4 = 0
2х1 – 3х2 + 5х3 + 4х4 = 0
– 2х1 + х2 + 3х3 + 6х4 = 0
|
| 11. |  3х1 – 8х2 – 7х3 – х4 = 0
–х1 + 7х2 – 5х3 – 3х1 – 8х2 – 7х3 – х4 = 0
–х1 + 7х2 – 5х3 –  х4 = 0
х1 + 6х2 – 3х3 + 5х4 = 0 х4 = 0
х1 + 6х2 – 3х3 + 5х4 = 0
| 12. |  3х1 – х2 + 4х3 + 2х4 = 0
–х1 – 2х2 – 7х3 – х4 = 0
5х1 – 4х2 – х3 + 3х4 = 0 3х1 – х2 + 4х3 + 2х4 = 0
–х1 – 2х2 – 7х3 – х4 = 0
5х1 – 4х2 – х3 + 3х4 = 0
|
| 13. |  х1 + 8х2 – 6х3 – 2х4 = 0
–2х1 – 3х2 + х3 – х4 = 0
–3х1 – 2х2 – 4х3 – 4х4 = 0 х1 + 8х2 – 6х3 – 2х4 = 0
–2х1 – 3х2 + х3 – х4 = 0
–3х1 – 2х2 – 4х3 – 4х4 = 0
| 14. |  3х1 + х2 + х3 – 3х4 = 0
х1 + 3х2 – 2х3 + 2х4 = 0
5х1 + 7х2 – 3х3 + х4 = 0 3х1 + х2 + х3 – 3х4 = 0
х1 + 3х2 – 2х3 + 2х4 = 0
5х1 + 7х2 – 3х3 + х4 = 0
|
| 15. |  –3х1 – 9х2 + 25х3 + х4 = 0
2х1 + 4х2 + 2х3 – 3х4 = 0
х1 – х2 + 9х3 – 5х4 = 0 –3х1 – 9х2 + 25х3 + х4 = 0
2х1 + 4х2 + 2х3 – 3х4 = 0
х1 – х2 + 9х3 – 5х4 = 0
| 16. |  3х1 – х2 + 2х3 + х4 = 0
–4х1 + 5х2 – 3х3 – х4 = 0
2х1 + 3х2 + х3 + 3х4 = 0 3х1 – х2 + 2х3 + х4 = 0
–4х1 + 5х2 – 3х3 – х4 = 0
2х1 + 3х2 + х3 + 3х4 = 0
|
| 17. |  –х1 – 3х2 + х3 – 8х4 = 0
2х1 – 4х2 + 5х3 – 12х4 = 0
4х1 + 2х2 + 3х3 + 2х4 = 0 –х1 – 3х2 + х3 – 8х4 = 0
2х1 – 4х2 + 5х3 – 12х4 = 0
4х1 + 2х2 + 3х3 + 2х4 = 0
| 18. |  2х1 + х2 – 4х3 + 2х4 = 0
4х1 – 9х2 + 2х3 + 4х4 = 0
–х1 + 5х2 – 3х3 – х4 = 0 2х1 + х2 – 4х3 + 2х4 = 0
4х1 – 9х2 + 2х3 + 4х4 = 0
–х1 + 5х2 – 3х3 – х4 = 0
|
| 19. |  2х1 – 4х2 – х3 + х4 = 0
х1 – 7х2 – 6х3 – 3х4 = 0
–3х1 + х2 – 4х3 – 5х4 = 0 2х1 – 4х2 – х3 + х4 = 0
х1 – 7х2 – 6х3 – 3х4 = 0
–3х1 + х2 – 4х3 – 5х4 = 0
| 20. |  х1 + 4х2 – 7х3 – 3х4 = 0
–х1 – 2х2 + 3х3 – х4 = 0
–х1 – 3х2 + 5х3 + х4 = 0 х1 + 4х2 – 7х3 – 3х4 = 0
–х1 – 2х2 + 3х3 – х4 = 0
–х1 – 3х2 + 5х3 + х4 = 0
|
| 21. |  2х1 – х2 – 3х3 = 0
х1 + 2х2 – 5х3 = 0
3х1 + х2 – 2х3 = 0 2х1 – х2 – 3х3 = 0
х1 + 2х2 – 5х3 = 0
3х1 + х2 – 2х3 = 0
| 22. |  3х1 + 2х2 – х3 = 0
2х1 – х2 + 3х3 = 0
х1 + 3х2 – 4х3 = 0 3х1 + 2х2 – х3 = 0
2х1 – х2 + 3х3 = 0
х1 + 3х2 – 4х3 = 0
|
| 23. |  5х1 + х2 – 7х3 – 5х4 + 2х5 = 0
2х1 – 2х2 – 3х3 – 7х4 + 2х5=0
3х1 + 9х2 –3х3 +27х4 –3х5=0 5х1 + х2 – 7х3 – 5х4 + 2х5 = 0
2х1 – 2х2 – 3х3 – 7х4 + 2х5=0
3х1 + 9х2 –3х3 +27х4 –3х5=0
| 24. | 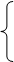 3х1 +9х2 – х3 – 3х4 = 0
х1 + 10х2 – 3х3 – 2х4 – х5= 0
2х1 + 19х2 –4х3 – 5х4 – х5= 0 3х1 +9х2 – х3 – 3х4 = 0
х1 + 10х2 – 3х3 – 2х4 – х5= 0
2х1 + 19х2 –4х3 – 5х4 – х5= 0
|
| 25. | 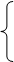 6х1 + 5х2 – 2х3 –х4 + 3х5 = 0
х1 – 3х2 +х3 – х4 –х5=0
2х1 + 3х2 +2х3 +х4 + х5=0 6х1 + 5х2 – 2х3 –х4 + 3х5 = 0
х1 – 3х2 +х3 – х4 –х5=0
2х1 + 3х2 +2х3 +х4 + х5=0
| 26. | 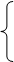 3х1 +5х2 – 2х3 + х4 – х5 = 0
х1 + х2 + 2х3 – х4 + х5= 0
2х1 + 3х2 – х3 = 0 3х1 +5х2 – 2х3 + х4 – х5 = 0
х1 + х2 + 2х3 – х4 + х5= 0
2х1 + 3х2 – х3 = 0
|
| 27. | 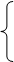 2х1 – 4х2 –22х3 –5х4 +5х5 = 0
5х1 – х2 +8х3 – 2х4 +2х5=0
3х1 – 3х2 –12х3 – 4х4 + 4х5=0 2х1 – 4х2 –22х3 –5х4 +5х5 = 0
5х1 – х2 +8х3 – 2х4 +2х5=0
3х1 – 3х2 –12х3 – 4х4 + 4х5=0
| 28. |  3х1 + 9х2 +2х3 –2х4 + х5 = 0
х1 + 6х2 – х3 + х4 +2х5 =0
х1 + 16х2 –6х3 + 6х4 + 7х5 =0 3х1 + 9х2 +2х3 –2х4 + х5 = 0
х1 + 6х2 – х3 + х4 +2х5 =0
х1 + 16х2 –6х3 + 6х4 + 7х5 =0
|
| 29. |  6х1 –9х2 +21х3 –3х4 –12х5=0
8х1–12х2 +28х3 –4х4 –16х5=0
2х1 –3х2 +7х3 – х4 – 4х5=0 6х1 –9х2 +21х3 –3х4 –12х5=0
8х1–12х2 +28х3 –4х4 –16х5=0
2х1 –3х2 +7х3 – х4 – 4х5=0
| 30. |  3х1 + 3х2 + 4х3 +5х4 – 4х5 = 0
2х1 + х2 +3х3 + х4 – 5х5 = 0
х1 + 3х2 – х3 + 6х4 – х5 =0 3х1 + 3х2 + 4х3 +5х4 – 4х5 = 0
2х1 + х2 +3х3 + х4 – 5х5 = 0
х1 + 3х2 – х3 + 6х4 – х5 =0
|
5 По координатам вершин пирамиды А1А2А3А4 найти:
1) длины ребер А1А2 и А1А3;
2) угол между ребрами А1А2 и А1А3;
3) площадь грани А1А2А3;
4) объем пирамиды;
5) уравнение прямой А1А2;
6) уравнение плоскости, проходящей через точку А4 и перпендикулярно вектору  ;
;
7) уравнение плоскости А1А2А4;
8) угол между прямой А1А2 и плоскостью А1А2А4.
| № варианта | Координаты вершин пирамиды |
| 1. | А1(–1; 2; 1), А2(–2; 2; 5), А3(–3; 3; 1), А4(–1; 4; 3) |
| 2. | А1(–2; 1; –1), А2 (–3; 1; 3), А3(–4; 2; –1), А4(– 2; 3; 1) |
| 3. | А1(l; 1; 2), А2 (0; 1; 6), А3(–l; 2; 2), А4(l; 3; 4) |
| 4. | А1(–1; –2; 1), А2 (–2; –2; 5), А3(–3; –1; 1), А4(–1; 0; 3) |
| 5. | А1(2; –1; 1), А2 (l; –1; 5), А3(0; 0; 1), А4(2; 1; 3) |
| 6. | А1(–l; 1; –2), А2 (–2; 1; 2), А3(–3; 2; –2), А4(–1; 3; 0) |
| 7. | А1(l; 2; 1), А2 (0; 2; 5), Аз(–1; 3; 1), А4(l; 4; 3) |
| 8. | А1(–2; –1; 1), А2 (–3; –1; 5), А3(–4; 0; 1), А4(–2; 1; 3) |
| 9. | А1(l; –1; 2), А2 (0; –1; 6), А3(–1; 0; 2), А4(l; 1; 4) |
| 10. | А1(1; –2; 1), А2(0; –2;5), А3(–l; –l; 1), А4(l; 0; 3) |
| 11. | А1(0; 3; 2), А2(–1; 3; 6); А3(–2; 4; 2), А4(0; 5; 4) |
| 12. | А1(–l; 2; 0), А2(–2; 2; 4), А3(–3; 3; 0), А4(–1;4;2) |
| А1(2; 2; 3), А2(l; 2; 7), А3(0; 3; 3), А4(2; 4; 5) | |
| А1(0; –1; 2), А2(–1; –1; 6), А3(–2; 0; 2), А4(0; 1; 4) | |
| 15. | А1(3; 0; 2), А2(2; 0; 6), А3(1; 1; 2), А4(3; 2; 4) |
| 16. | А1(0; 2; –1), А2(–1; 2; 3), А3(–2; 3; 7), А4(0; 4; 1) |
| 17. | А1(2; 3; 2), А2(l; 3; 6), А3(0; 4; 2), А4(2; 5; 4) |
| 18. | А1(–1; 0; 2), А2(–2; 0; 6), А3(–3; 1; 2), А4(–1; 2; 4) |
| 19. | А1(2; 0; 3), А2(1; 0; 7), А3(0; 1; 3), А4(2; 2; 5) |
| 20. | А1(2; –1; 2), А2(1; –1; 6), А3(0; 0; 2), А4(2; 1; 4) |
| 21. | А1(4; 2; 5), А2 (0; 7; 2), А3(0; 2; 7), А4(1; 5; 0) |
| 22. | А1(4; 4; 1 0), А2 (4; 10; 2), А3(2; 8; 4), А4(9; 6; 4) |
| 23. | А1(4; 6; 5), А2(6; 9; 4), А3(2; 10; 10), А4(7; 5; 9) |
| 24. | А1(3; 5; 4), А2(8; 7; 4), А3(5; 10; 4), А4(4; 7; 8) |
| 25. | А1(10; 6; 6), А2(–2; 8; 2), А3(6; 8; 9), А4(7; 10; 3) |
| 26. | А1(1; 8; 2), А2(5; 2; 6), А3(5; 7; 4), А4(4; 10; 9) |
| 27. | А1(6; 6; 5), А2(4; 9; 5), А3(4; 6; 11), А4(6; 9; 3) |
| 28. | А1(7; 2; 2), А2(5; 7; 7), А3(5; 3; 1), А4(2; 3; 7) |
| 29. | А1(8; 6; 4), А2(10; 5; 5), А3(5; 6; 8), А4(8; 10; 7) |
| 30. | А1(7; 7; 3), А2(6; 5; 8), А3(3; 5; 8), А4(8; 4; 1) |
6. Даны векторы  в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы  образуют базис и найти координаты вектора
образуют базис и найти координаты вектора  в этом базисе.
в этом базисе.
| № варианта | Векторы |
| 1. |  , , 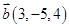
|
| 2. |  , , 
|
| 3. |  , , 
|
| 4. |  , , 
|
| 5. |  , , 
|
| 6. | 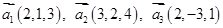 , , 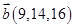
|
| 7. | 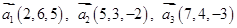 , , 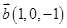
|
| 8. |  , , 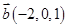
|
| 9. |  , , 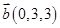
|
| 10. |  , , 
|
| 11. | 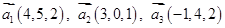 , , 
|
| 12. |  , , 
|
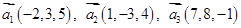 , , 
| |
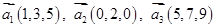 , , 
| |
| 15. |  , , 
|
| 16. |  , , 
|
| 17. |  , , 
|
| 18. |  , , 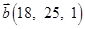
|
| 19. |  , , 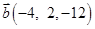
|
| 20. | 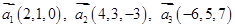 , , 
|
| 21. |  , , 
|
| 22. |  , , 
|
| 23. |  , , 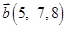
|
| 24. |  , , 
|
| 25. | 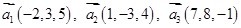 , , 
|
| 26. |  , , 
|
| 27. |  , , 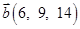
|
| 28. |  , , 
|
| 29. |  , , 
|
| 30. | 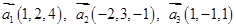 , , 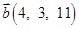
|
Задача 7. По данным точкам найти: 1) уравнение прямых АВ и АС с угловым коэффициентом и общее уравнение каждой прямой; 2) угол между прямыми АВ и АС
| № варианта | Координаты точек |
| 1. | А(–3; –2), В(0; 10), С(6; 2) |
| 2. | А(1; 1), В(4; 13), С(10; 5) |
| 3. | А(0; 3), В(3; 15), С(9; 7) |
| 4. | А(–2; 0), В(1; 12), С(7; 4) |
| 5. | А(2; –1), В(5; 11), С(11; 3) |
| 6. | А(3; –3), В(6; 9), С(12; 1) |
| 7. | А(–1; 2), В(2; 14), С(8; 6) |
| 8. | А(5; –4), В(8; 8), С(14; 0) |
| 9. | А(–4; 5), В(–1; 17), С(5; 9) |
| 10. | А(4; 4), В(7; 16), С(13; 8) |
| 11. | А(3; 2), В(0; –10), С(–1; 2) |
| 12. | А(0; 2), В(–2; 1), С(4; –2) |
| А(–4; 2), В(–1; 0), С(–5; 1) | |
| А(3; –1), В(0; 0), С(–7; 1) | |
| 15. | А(–6; –1), В(0; 4), С(–3; 6) |
| 16. | А(0; 6), В(6; 0), С(1; 2) |
| 17. | А(8; –1), В(–4; 1), С(6; –2) |
| 18. | А(–3; –2), В(0; 10), С(6; 2) |
| 19. | А(–1; 2), В(0; 5), С(5; 0) |
| 20. | А(5; 2), В(–1; 4), С(0; 2) |
| 21. | А(2; 3), В(1; 5), С(–3; 2) |
| 22. | А(0; –2), В(–2; 0), С(5; 5) |
| 23. | А(4; 4), В(0; 1), С(–2; 0) |
| 24. | А(–3; –3), В(5; 1), С(0; 2) |
| 25. | А(4; 5), В(5; 4), С(0; 1) |
| 26. | А(0; –2), В(–2; 3), С(4; –6) |
| 27. | А(–5; –1), В(3; 1), С(0; 4) |
| 28. | А(3; 3), В(10; 0), С(5; –2) |
| 29. | А(1; 2), В(7; 0), С(3; –1) |
| 30. | А(5; –4), В(3; 0), С(–4; 1) |
Задача 8 Найти собственные значения и собственные векторы матрицы.
1. 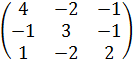 .
.
2.  .
.
3. 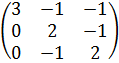 .
.
4. 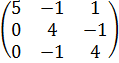 .
.
5. 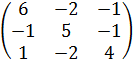 .
.
6. 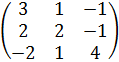 .
.
7. 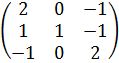 .
.
8.  .
.
9.  .
.
10. 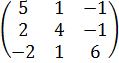 .
.
11.  .
.
12. 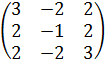 .
.
13. 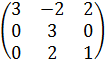 .
.
14.  .
.
15.  .
.
16. 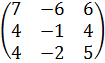 .
.
17.  .
.
18. 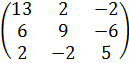 .
.
19.  .
.
20. 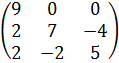 .
.
21.  .
.
22. 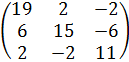 .
.
23.  .
.
24.  .
.
25.  .
.
26.  .
.
27.  .
.
28.  .
.
29. 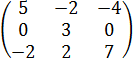 .
.
30.  .
.
31. 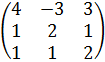 .
.
Задача 9.. Привести квадратичную форму к каноническому виду.
1. 4  - 3
- 3  - 4x1x2 – 4x1x3 + 8x2x3.
- 4x1x2 – 4x1x3 + 8x2x3.
2. 4  + 4
+ 4  +
+  – 2x1x2 + 2
– 2x1x2 + 2 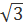 x2x3.
x2x3.
3. 2  + 2x2 + 2
+ 2x2 + 2  + 8x1x2 + 8x1x3 – 8x2x3.
+ 8x1x2 + 8x1x3 – 8x2x3.
4. 2  + 9
+ 9  + 2
+ 2  – 4x1x2 + 4x2x3.
– 4x1x2 + 4x2x3.
5. -4  - 4
- 4  + 2
+ 2  – 4x1x2 + 8x1x3 – 8x2x3.
– 4x1x2 + 8x1x3 – 8x2x3.
6.  +
+  + 4
+ 4  + 2x1x2 - 2
+ 2x1x2 - 2 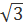 x2x3.
x2x3.
7. 4  + 4
+ 4  +
+  + 2x1x2 – 4x1x3 + 4x2x3.
+ 2x1x2 – 4x1x3 + 4x2x3.
8. 3  +
+  -
- 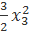 + 2
+ 2 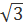 x1x2 – x1x3 +
x1x2 – x1x3 + 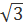 x2x3.
x2x3.
9. -  -
-  - 3
- 3  – 2x1x2 – 6x1x3 + 6x2x3.
– 2x1x2 – 6x1x3 + 6x2x3.
10.  - 7
- 7  +
+  – 4x1x2 – 2x1x3 – 4x2x3.
– 4x1x2 – 2x1x3 – 4x2x3.
11. 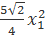 +
+  +
+  +
+ 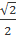 x1x2 + x1x3 + x2x3.
x1x2 + x1x3 + x2x3.
12. 3  - 7
- 7  + 3
+ 3  + 8x1x2 – 8 x1x3 – 8x2x3.
+ 8x1x2 – 8 x1x3 – 8x2x3.
13.  + 5
+ 5  +
+  – 4x1x2 + 5
– 4x1x2 + 5  x1x3 +
x1x3 +  x2x3.
x2x3.
14.  +
+  +
+  –
–  x1x2 -
x1x2 - 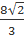 x2x3.
x2x3.
15. 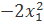 + 2
+ 2  - 2
- 2  – 4x1x2 + 5
– 4x1x2 + 5  x1x3 +
x1x3 +  x2x3.
x2x3.
16. 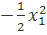 + 5
+ 5  -
- 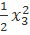 – 4x1x2 + 3x1x3 + 4x2x3.
– 4x1x2 + 3x1x3 + 4x2x3.
17.  +
+  +
+  – 4x1x3 + 4x2x3.
– 4x1x3 + 4x2x3.
18. -2  + 2
+ 2  - 2
- 2  + 4x1x2 – 6x1x3 + 4x2x3.
+ 4x1x2 – 6x1x3 + 4x2x3.
19. 2  + 3
+ 3  + 2
+ 2  – 8x1x2 - 4
– 8x1x2 - 4  x1x3 + 2
x1x3 + 2  x2x3.
x2x3.
20. -4  +
+  - 4
- 4  + 4x1x2 – 4x1x3 + 4x2x3.
+ 4x1x2 – 4x1x3 + 4x2x3.
21. 10  + 14
+ 14  + 7
+ 7  – 10x1x2 –
– 10x1x2 –  x1x3 – 5
x1x3 – 5  x2x3.
x2x3.
22. 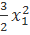 - 5
- 5  +
+ 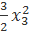 + 4x1x2 – x1x3 – 4x2x3.
+ 4x1x2 – x1x3 – 4x2x3.
23.  +
+  +
+  + 4x1x2 + 2
+ 4x1x2 + 2  x1x3 – 2
x1x3 – 2  x2x3.
x2x3.
24. 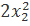 - 3
- 3  - 2
- 2 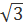 x1x2 – 4x1x3 +4
x1x2 – 4x1x3 +4 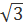 x2x3.
x2x3.
25.  +
+  +
+  +
+  x1x2 +
x1x2 + 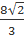 x2x3.
x2x3.
26.  +
+  + 8x1x2 + 4
+ 8x1x2 + 4  x1x3 – 2
x1x3 – 2  x2x3.
x2x3.
27.  + 13
+ 13  + 5
+ 5  + 4x1x2 + 8x2x3.
+ 4x1x2 + 8x2x3.
28. 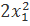 + 2
+ 2  + 2
+ 2  +
+  x1x2 +
x1x2 +  x2x3.
x2x3.
29.  + 4
+ 4  + 2
+ 2  – 4x1x2 – 2
– 4x1x2 – 2  x1x3 + 4
x1x3 + 4  x2x3.
x2x3.
30. 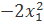 + 5
+ 5  - 2
- 2  + 4x1x2 + 4x2x3.
+ 4x1x2 + 4x2x3.
31. 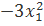 + 9
+ 9  + 3
+ 3  + 2x1x2 + 8x1x3 + 4x2x3.
+ 2x1x2 + 8x1x3 + 4x2x3.