Контрольная работа для студентов заочного отделения,
Группы 2522, 2523, 2524, 2526.
Семестр 2015/2016 уч.год. Преподаватель: Макусева Т.Г.
Указания по выполнению контрольной работы.
Вариант определить по двум последним цифрам номера зачетной книжки
1. На обложке тетради необходимо написать фамилию, имя, отчество, курс, группу, номер студенческого билета, вариант контрольной работы и дату сдачи ее в институт.
2. Решение задач располагать в порядке номеров, указанных в заданиях, сохраняя их номер.
3. Перед решением каждой задачи выписать полностью условие.
4. Решение каждой задачи сопровождать объяснениями и заканчивать ответом.
5. Оформление решений производить аккуратно, с минимальным количеством исправлений. Оставить поля для замечаний проверяющего.
6. Для решения заданий контрольной работы рекомендуется использовать лекции, а также следующую литературу:
Для выполнения контрольной работы можно использовать разобранные ниже примеры, лекции, а также любые учебники в содержании которых имеется интегральное исчисление.
Тема «Интегральное и дифференциальное исчисление функций одной и нескольких переменных».
Обратите внимание, что в контрольной работе 5 задач.
Задача 1.
В задаче найти указанные неопределенные интегралы.
1. а)  ; б)
; б)  ; в)
; в)  .
.
2. а)  ; б)
; б)  ; в)
; в)  .
.
3. а)  ; б)
; б)  ; в)
; в)  .
.
4. а)  ; б)
; б)  ; в)
; в)  .
.
5. а)  ; б)
; б)  ; в)
; в)  .
.
6. а)  ; б)
; б)  ; в)
; в)  .
.
7. а)  ; б)
; б)  ; в)
; в)  .
.
8. а)  ; б)
; б)  ; в)
; в)  .
.
9. а)  ; б)
; б)  ; в)
; в)  .
.
10. а)  ; б)
; б)  ; в)
; в)  .
.
11. а)  ; б)
; б)  ; в)
; в)  .
.
12. а)  ; б)
; б)  ; в)
; в)  .
.
13. а)  ; б)
; б)  ; в)
; в)  .
.
14. а) 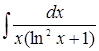 ; б)
; б)  ; в)
; в)  .
.
15. а)  ; б)
; б)  ; в)
; в) 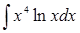 .
.
16. а)  ; б)
; б)  ; в)
; в)  .
.
17. а)  ; б)
; б)  ; в)
; в) 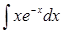 .
.
18. а)  ; б)
; б)  ; в)
; в)  .
.
19. а)  ; б)
; б)  ; в)
; в)  .
.
20. а)  ; б)
; б)  ; в)
; в)  .
.
21. а)  ; б)
; б)  ; в)
; в)  .
.
22. а)  ; б)
; б)  ; в)
; в)  .
.
23. а)  ; б)
; б)  ; в)
; в)  .
.
24. а)  ; б)
; б)  ; в)
; в)  .
.
25. а)  ; б)
; б)  ; в)
; в)  .
.
26. а)  ; б)
; б)  ; в)
; в)  .
.
27. а) 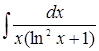 ; б)
; б)  ; в)
; в)  .
.
Примеры решения задачи 1.
а) Найти  .
.
Решение. Применяя подстановку  , приведем данный интеграл к табличному интегралу 2. Положим
, приведем данный интеграл к табличному интегралу 2. Положим  , тогда
, тогда  .
.
 .
.
а1) Найти  .
.
Применяя подстановку  , приведем данный интеграл к формуле 10.
, приведем данный интеграл к формуле 10.
Положим  , тогда
, тогда  .
.
 .
.
в1) Найти 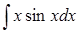 .
.
Принимаем  и
и  ; тогда
; тогда  и
и 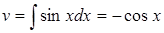 , следовательно
, следовательно  .
.
в2) Найти  .
.
Принимаем  и
и  ; тогда
; тогда  и
и  . Применяя формулу интегрирования по частям, будем иметь:
. Применяя формулу интегрирования по частям, будем иметь:

в3) Найти  .
.
Принимаем  и
и  ; тогда
; тогда  и
и  , следовательно,
, следовательно,

б) Найти интеграл  .
.
Преобразуем знаменатель дроби, стоящей под знаком интеграла, следующим образом:
 .
.
Тогда после подстановки  получаем
получаем
 =
=

 =
=

При этом при вычислении интеграла 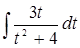 мы воспользовались заменой переменной
мы воспользовались заменой переменной  . Тогда
. Тогда  , откуда
, откуда

Задача 2. Вычислить определенный интеграл.





Пример решения задачи 2. Вычислить определенный интеграл.
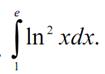











Задача 3.


3.21.  .
.
3.22.  .
.
3.23.  .
.
3.24.  .
.
3.25.  .
.
3.26.  .
.
3.27.  .
.
3.28  .
.
3.29.  .
.
3.30.  .
.
Пример решения задачи 3.






Пример решения:
Исследовать на экстремум функцию  .
.
На первом шаге, в соответствие с достаточным условием экстремума функции двух переменных, найдем точки, удовлетворяющие условию:

Частные производные первого порядка от функции  равны:
равны:

Приравняем их к нулю и решим систему уравнений:

Выпишем отдельно первое уравнение системы и найдем его корни:
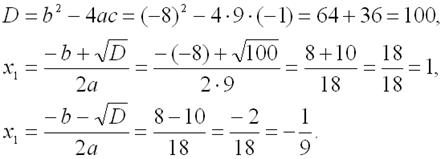
Подставим найденные значения переменной во второе уравнение системы:
 и
и 
Таким образом, получили две точки  и
и  , в которых будет продолжено исследование функции на экстремум.
, в которых будет продолжено исследование функции на экстремум.
На втором шаге найдем все вторые частные производные от функции На втором шаге найдем все вторые частные производные от функции z:
Для точки 

Так как дискриминант больше нуля и
 , то функция z имеет минимум в точке
, то функция z имеет минимум в точке  .
.
2) Для точки 

Так как дискриминант меньше нуля, то функция z не имеет в точке  ни минимума, ни максимума.
ни минимума, ни максимума.
Ответ: в точке  функция
функция  имеет минимум
имеет минимум  .
.
Задача 4. Вычислить площадь плоской фигуры с помощью определенного интеграла. Сделать рисунок.



4/21.  .
.
4.22.  .
.
4.23.  .
.
4.24.  .
.
4.25.  .
.
4.26.  .
.
4.27.  .
.
4.28.  .
.
4.29.  .
.
4.30.  .
.
Пример решения задачи 4. Вычислить площадь фигуры, ограниченной линиями  ,
,  (рис. 8).
(рис. 8).
Решение. Площадь  фигуры, ограниченной сверху и снизу непрерывными линиями
фигуры, ограниченной сверху и снизу непрерывными линиями  и
и 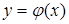 , пересекающимися в точках с абсциссами
, пересекающимися в точках с абсциссами  и
и  , определяется по формуле
, определяется по формуле
 . (1)
. (1)
 Для нахождения точек пересечения данных линий решаем систему уравнений
Для нахождения точек пересечения данных линий решаем систему уравнений

откуда  . Применяя формулу (1), получим:
. Применяя формулу (1), получим:

Задача 5. Кратные интегралы, их приложения
Изменить порядок интегрирования. Сделать чертеж области интегрирования.






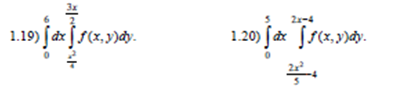
22)  23)
23)  24)
24)  25)
25) 
26) 
27) 

