параллельно-последовательных структур 
4.5.3.2. Система с параллельным соединением элементов
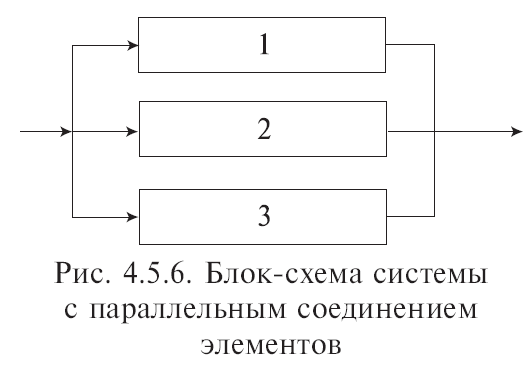
На рис. 4.5.6 представлено параллельное
соединение элементов 1,
2, 3. Это означает, что устройство,
состоящее из этих элементов, переходит
в состояние отказа после отказа
всех элементов при условии,
что все элементы системы находятся
под нагрузкой, а отказы элементов
статистически независимы.
Условие работоспособности устройства можно сформулировать следующим
образом: устройство работоспособно, если работоспособен элемент 1,
или элемент 2, или элемент 3, или элементы 1 и 2, 1 и 3, 2 и 3, 1 и 2 и 3.
ПРИМЕР 4.5.5. Предохранительное устройство, обеспечивающее безопасность
работы системы под давлением, состоит из трех дублирующих друг
друга клапанов. Надежность каждого из них р = 0,9. Клапаны независимы
в смысле надежности. Найти надежность устройства.
Решение. По формуле (4.5.10) P =1−(1−0,9)3 =0,999.
ПРИМЕР 4.5.6. Предположим, что два одинаковых вентилятора в системе
очистки отходящих газов работают параллельно, причем если один из них
выходит из строя, то другой способен работать при полной системной нагрузке
без изменения своих надежностных характеристик.
Требуется найти безотказность системы в течение 400 ч (продолжительность
выполнения задания) при условии, что интенсивности отказов двигателей
вентиляторов постоянны и равны λ = 0,0005 ч–1
, отказы двигателей
статистически независимы и оба вентилятора начинают работать в момент
времени t = 0.
Решение. В случае идентичных элементов формула (4.5.12) принимает
вид:
P (t)=2exp(−λ t) −exp(−2λ t).
Поскольку λ = 0,0005ч-1 и t = 400 ч, то:
P (400)=2exp(−0,0005. 400) − exp(−2. 0,0005. 400) = 0,9671.
Среднюю наработку на отказ находим, используя (4.5.13):
T 0=1/λ(1/1+1/2) =1/λ. 3 / 2 = 1,5 / 0,0005 = 3000 ч.
4.5.3.3. Способы преобразования сложных структур
Относительная простота расчетов надежности, основанных на использовании
параллельно-последовательных структур, делают их самыми распространенными
в инженерной практике. Однако не всегда условие работоспособности
можно непосредственно представить параллельно-последовательной
структурой. В этом случае можно сложную структуру заменить ее эквивалентной
параллельно-последовательной структурой. К таким преобразованиям относятся:
Существо способа преобразования с помощью эквивалентной замены
треугольника на звезду и обратно заключается в том, что узел сложной конфигурации
заменяется на узел другой, более простой конфигурации, но при
этом подбираются такие характеристики нового узла, что надежности преобразуемой
цепи сохранялись прежними.
Пусть, например, требуется заменить
треугольник (рис. 4.5.7, а)
звездой (рис. 4.5.7, б) при условии,
что вероятность отказа элемента a
равна q 13, элемента b равна q 12, элемента
c — q 23. Переход к соединению
звездой не должен изменить
надежность цепей 1—2, 1—3, 2—3.
Поэтому значение вероятностей отказов
элементов звезды q 1, q 2, q 3
должны удовлетворять следующим
равенствам: 
ПРИМЕР 4.5.7. Определить вероятность безотказной работы устройства,
структурная схема которого изображена на рис. 4.5.3, б, если известно, что
вероятности безотказной работы каждого из элементов схемы равны 0,9,
а вероятности отказов равны 0,1.
Решение.
1. Преобразуем соединение элементов
1, 2, 5 в треугольник
(рис. 4.5.8, а), в звезду (рис. 4.5.8, б).
2. Определим эквивалентные
значения вероятности отказов для
новых элементов a, b, c: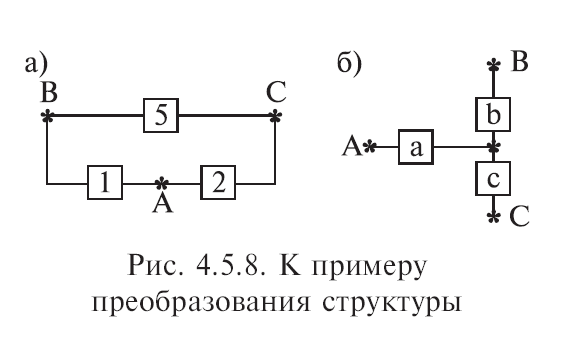 
ПРИМЕР 4.5.8. Решить предыдущий пример методом разложения сложной
структуры.
Решение.
1. В качестве базового элемента примем элемент 5 (рис. 4.5.3, б).
2. Закоротим базовый элемент, т. е. сделаем допущение об абсолютной
его проводимости. Присоединим к полученной структуре последовательно
базовый элемент с характеристикой его надежности р 5. В результате вместо
исходной структуры получим новую структуру (рис. 4.5.10, а).
3. Произведем обрыв базового элемента, т. е. сделаем предположение
об его абсолютной ненадежности (непроводимости). К полученной структуре
присоединим последовательно базовый элемент с характеристикой его
ненадежности(1 − p 5). В результате получим структуру (рис. 4.5.10, б).
ПРИМЕР 4.5.9. Определить вероятность безотказной работы устройства,
структурная схема которого изображена на рис. 4.5.3, б, если известно, что
вероятности безотказной работы каждого из элементов схемы равны 0,9.
Решение.
Так как все элементы идентичны, воспользуемся формулой (4.5.18), с ее
помощью получаем:
P =2Ч0,95−5Ч0,94+2Ч0,93+2Ч0,92≈0,978
