Производная функции и её применение
Определение производной функции. Вычисление производных основных элементарных функций. Вычисление производных сложных функций
Пусть функция f(x) определена в некоторой окрестности точки 
.
Определение: Производной функции y=f(x) по аргументу x называется предел отношения ее приращения ∆f(x) к приращению ∆x аргумента x, когда приращение аргумента стремится к нулю:
.
Если этот предел конечный, то функция y=f(x) называется дифференцируемой в точке x. Если же этот предел есть ∞, то говорят, что функция y=f(x) имеет в точке x бесконечную производную.
Алгоритм отыскания производной y = f(x ):
1. Находим f(x).
2. Находим f(x+∆x).
3. Вычисляем ∆f = f(x+∆x) – f(x).
4. Составляем отношение 
при ∆x→0.
Пример 1. Найти производную функции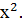 
Решение.
1) f(x) = 
2) f(x+∆x) = 
.
3) ∆f = f(x+∆x) – f(x) =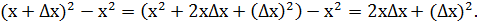 
4) 
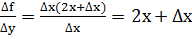
Итак, 
.
Необходимое условие существования производной вытекает из следующей теоремы.
Теорема. Если функция f(x) дифференцируема в точке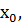 
то она непрерывна в этой точке.
Основные правила дифференцирования
Непосредственное вычисление производной функции с помощью предела в большинстве случаев представляет собой громоздкие вычисления. Значительно проще вычислять производные, применяя правила дифференцирования.
Обозначения: С−постоянная; х−аргумент; u, v, w−функции от х, имеющие производные.
Правило 1. Производная постоянной
Правило 2. Производная произведения постоянной на функцию
Правило 3. Производная алгебраической суммы
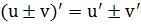
Правило 4. Производная произведения
Правило 5. Производная частного (дроби)
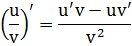
Частные случаи
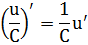
Таблица основных формул дифференцирования
1. 
2. 
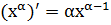
3. 
4. 
5. 
6. 
7. 
8. 
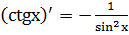
9. 
10. 
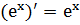
11. 
12. 
13. 
14. 
15. 
16. 
Пример 2. Найти производную функции 
.
Решение. Запишем формулу в виде
= 
Пример 3. Найти производную функции 
.
Решение. Применяя правило производная произведения и формулы (2) и (15) получим
.
Пример 4. Найти производную функции 
.
Решение. Применяя правило производная частного и формулы (1) и (5) получим
Производная сложной функции
Если переменная y зависит от переменной u, а переменная u в свою очередь от переменной x, т.е. y=f(u(x)), то y называют сложной функцией от x. Например, y=sin 
– сложная функция от x, т.к. синус зависит от промежуточного аргумента х5.
Производная сложной функции определяется по формуле
,
т.е. производная сложной функции равна произведению производной данной функции по промежуточному аргументу на производную этого аргумента по независимой переменной. Аналогично формула верна и для сложных функций, которые задаются с помощью цепочки, содержащей три звена и более.
Пример 5. Найти производную 
Решение.
y’= 
.
Пример 6. Найти производную функции y=sin(3x-5).
Решение. 
.
Пример 7. Найти производную функции у= 
.
Решение. 
.
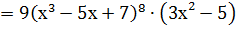Пример 8. Найти производную функции у= 
.
Решение. Эта функция также является сложной степенной функцией, а именно у= 
, где u=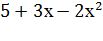 
. Поэтому
.
Пример 9. Найти производную функции у= 
.
Решение.
= 
.
Пример 10. Дана функция f(x)= 
. Найти 
.
Решение.
.
Вычислим значение производной при х=1
,
. [1]
Упражнения для закрепления
1. 
2. 
3. 
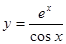
4. 
5. 
6. 
7. 
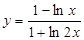
8. 
9. 
10. 
11. 
12. 
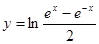
Контрольные вопросы
1. Дать определение производной функции.
2. Что называется приращением аргумента, приращением функции?
3. Как найти производную суммы или разности?
4. Как найти производную произведения?
5. Как найти производную частного двух функций?
6. Дать определение дифференциала функции.